Chapter 7, Problem 72RE

Solution

a.

To determine: The matrix of order 3 cross 2 that estimates the number of males and females in these three state.

The obtained matrix is $\left[\begin{array}{cc}18.3& 19\\ 9.2& 9.6\\ 0.5& 0.6\end{array}\right]$ .

Given Information:

The table is defined,

State	Population (millions)
California	37.3
Florida	18.8
Rhode Island	1.1

Calculation:

Consider the given table,

State	Population (millions)
California	37.3
Florida	18.8
Rhode Island	1.1

Now, refer Table 7.10 U.S. Male and Female Population Data, 1900−2010 to find the population.

  

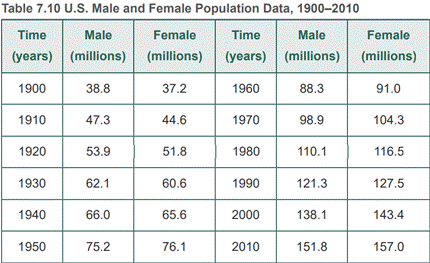
Now, use the ratio of male to female in the year 2010 as it is given $151.8:157.0$ .

First, find for the California.

  $\begin{array}{c}M:\frac{151.8}{151.8+157}\cdot 37.3\\ =18.3\end{array}$

And,

  $\begin{array}{c}F:37.3-18.3\\ =19.0\end{array}$

Find for the Florida.

  $\begin{array}{c}M:\frac{151.8}{151.8+157}\cdot 18.8\\ =9.2\end{array}$

And,

  $\begin{array}{c}F:18.8-9.2\\ =9.6\end{array}$

Find for the Rhode Island.

  $\begin{array}{c}M:\frac{151.8}{151.8+157}\cdot 1.1\\ =0.5\end{array}$

And,

  $\begin{array}{c}F:1.1-0.5\\ =0.6\end{array}$

Now, make the matrix of the given order.

  $\begin{array}{l}\text{ M F}\\ \left[\begin{array}{cc}18.3& 19\\ 9.2& 9.6\\ 0.5& 0.6\end{array}\right]\end{array}$

Therefore, the obtained matrix is $\left[\begin{array}{cc}18.3& 19\\ 9.2& 9.6\\ 0.5& 0.6\end{array}\right]$ .

b.

To determine: The 3 cross 2 matrix form the given table.

The obtained result is $\left[\begin{array}{cc}25.0& 11.4\\ 21.3& 17.3\\ 22.3& 14.3\end{array}\right]$ .

Given Information:

The table is defined,

State	%Pop. Under 18 years	%Pop. 65 Years or older
California	25.0	11.4
Florida	21.3	17.3
Rhode Island	22.3	14.3

Calculation:

Consider the given table,

State	%Pop. Under 18 years	%Pop. 65 Years or older
California	25.0	11.4
Florida	21.3	17.3
Rhode Island	22.3	14.3

From the given table the required matrix is defined as,

  $\left[\begin{array}{cc}25.0& 11.4\\ 21.3& 17.3\\ 22.3& 14.3\end{array}\right]$

Hence, the obtained matrix is $\left[\begin{array}{cc}25.0& 11.4\\ 21.3& 17.3\\ 22.3& 14.3\end{array}\right]$ .

c.

To calculate: The multiplication of the matrix in part (b) with the scaler.

The obtained matrix is $\left[\begin{array}{cc}0.25& 0.114\\ 0.213& 0.173\\ 0.223& 0.143\end{array}\right]$ .

Given Information:

The given scaler for multiplication is $0.001$ .

Calculation:

Consider the given table,

Refer the matrix from part (b).

  $\left[\begin{array}{cc}25.0& 11.4\\ 21.3& 17.3\\ 22.3& 14.3\end{array}\right]$

Multiply the matrix by $0.01$ .

  $\begin{array}{c}0.01\cdot \left[\begin{array}{cc}25.0& 11.4\\ 21.3& 17.3\\ 22.3& 14.3\end{array}\right]=\left[\begin{array}{cc}25.0\left(0.01\right)& 11.4\left(0.01\right)\\ 21.3\left(0.01\right)& 17.3\left(0.01\right)\\ 22.3\left(0.01\right)& 14.3\left(0.01\right)\end{array}\right]\\ =\left[\begin{array}{cc}0.25& 0.114\\ 0.213& 0.173\\ 0.223& 0.143\end{array}\right]\end{array}$

Hence, the obtained matrix is $\left[\begin{array}{cc}0.25& 0.114\\ 0.213& 0.173\\ 0.223& 0.143\end{array}\right]$ .

d.

To calculate: The matrix multiplication of the transpose of part (c) and part (a).

The total population of males and females that are under 18 years and 65 years or older for the three states

Given Information:

Refer the matrix form part (a) and part (c).

  $\left[\begin{array}{cc}18.3& 19\\ 9.2& 9.6\\ 0.5& 0.6\end{array}\right]$ and $\left[\begin{array}{cc}0.25& 0.114\\ 0.213& 0.173\\ 0.223& 0.143\end{array}\right]$

Calculation:

Consider the given information,

Find the transpose the matrix part (a).

  ${\left[\begin{array}{cc}18.3& 19\\ 9.2& 9.6\\ 0.5& 0.6\end{array}\right]}^T=\left[\begin{array}{ccc}18.3& 9.2& 0.5\\ 19& 9.6& 0.6\end{array}\right]$

Now, find the multiplication.

  $\left[\begin{array}{ccc}18.3& 9.2& 0.5\\ 19& 9.6& 0.6\end{array}\right]\cdot \left[\begin{array}{cc}0.25& 0.114\\ 0.213& 0.173\\ 0.223& 0.143\end{array}\right]=\left[\begin{array}{cc}6.6& 6.9\\ 3.7& 3.9\end{array}\right]$

Which is indicating the total population of males and females that are under 18 years and 65 years or older for the three states.

Therefore, the obtained matrix is $\left[\begin{array}{cc}6.6& 6.9\\ 3.7& 3.9\end{array}\right]$

e.

To calculate: The number of males under the age 18 lived in these three states in the year 2010 and number of females age 65 or older lived these three states.

The number of males under the age 18 is $6.6$ million in the year 2010 and number of females age 65 or older is $3.9$ million.

Given Information:

Refer the matrix obtained from the part (b).

  $\left[\begin{array}{cc}6.6& 6.9\\ 3.7& 3.9\end{array}\right]$

Calculation:

Consider the given information,

  $\left[\begin{array}{cc}6.6& 6.9\\ 3.7& 3.9\end{array}\right]$

The first entry of the above matrix is representing the number males under age 18, that is $6.6$ million and the last entry $a_{22}$ is representing the number of females age 65 or older that is $3.9$ million.

Therefore, the number of males under the age 18 is $6.6$ million in the year 2010 and number of females age 65 or older is $3.9$ million.