
Concept explainers
(b)
The null and alternative hypotheses for the consumption of proteins.
(b)
Answer to Problem 72E
Solution: The null and alternative hypotheses are formulated as
Explanation of Solution
Therefore, the hypotheses are formulated as:
In the above hypotheses
To find: The null and alternative hypotheses for the consumption of carbohydrates.
Answer to Problem 72E
Solution: The null and alternative hypotheses are formulated as
Explanation of Solution
Calculation: The significance test is to compare the two groups in terms of consumption of carbohydrates. Hence, the hypothesis is that the consumption of carbohydrates in the two groups is the same against the alternative that the consumption of carbohydrates in the two groups is not the same.
Therefore, the hypotheses are formulated as
In the above hypothesis
(c)
To find: The test statistic with the degrees of freedom and the p-value for consumption of proteins.
(c)
Answer to Problem 72E
Solution: The t – test statistic is obtained as 2.47 and p – value as 0.0144 for 199 degrees of freedom for consumption of proteins.
Explanation of Solution
Calculation: The two-sample t – test statistic for the hypothesis formulated in part (a) is defined as:
Where,
The difference of means is considered as 0 in the null hypothesis. Substitute the provided values in the above defined formula to compute the two sample t statistic. So,
The p-value for the provided one–sided test is calculated as
So, the degrees of freedom are 199. The Excel function to determine the p- value from t-test statistic is displayed in the attached screenshot,
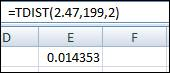
Therefore, the p-value is obtained as 0.0144.
To explain: The conclusion of the performed significance test.
Answer to Problem 72E
Solution: There is significant difference between the early eaters and late eaters in terms of consumption of proteins.
Explanation of Solution
To find: The test statistic with the degrees of freedom and the p-value for the consumption of carbohydrates.
Answer to Problem 72E
Solution: The t – test statistic is obtained as 0.29 and p – value as 0.772 for 199 degrees of freedom for carbohydrates consumption.
Explanation of Solution
Calculation: The two-sample t – test statistic for the hypothesis formulated in part (a) is defined as:
Where,
The difference of true means is considered as 0 according to the null hypothesis. Substitute the provided values in the above defined formula to compute the two sample t statistic. So,
The p-value for the provided one-sided test is calculated as
So, the degrees of freedom are 199. The Excel function to determine the p- value from t-test statistic is displayed in the attached screenshot,
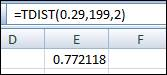
Therefore, the p-value is obtained as 0.772.
The conclusion of the performed significance test.
Answer to Problem 72E
Solution: There is no significant difference between the early eaters and late eaters in terms of consumption of carbohydrates.
Explanation of Solution
(d)
To find: A 95% confidence interval for the difference of means between early eaters and late eaters in terms of consumption of proteins.
(d)
Answer to Problem 72E
Solution: A required 95% confidence interval is
Explanation of Solution
Calculation: The formula for confidence interval for the difference between the means is defined as:
where
According to the Table D provided in the Appendix, the critical value for a two-tailed test at 95% confidence level is 1.962 for 199 degrees of freedom. Substitute the provided values in the above-defined formula to determine the 95% confidence interval for the difference between the early eaters and late eaters in terms of consumption of proteins. So,
Therefore, the 95% confidence interval for the difference between the means is obtained as
To explain: The comparison of information from the obtained confidence interval with the information given by the significance test.
Answer to Problem 72E
Solution: The information provided by both confidence interval and the significance test shows that there is a significant difference between the two means of proteins.
Explanation of Solution
To find: A 95% confidence interval for the difference of means between early eaters and late eaters in terms of consumption of carbohydrates.
Answer to Problem 72E
Solution: A required confidence interval is
Explanation of Solution
Calculation: The formula for confidence interval for the difference between the means is defined as:
where
According to the Table D provided in the Appendix, the critical value for a two-tailed test at 95% confidence level is 1.962 for 199 degrees of freedom. Substitute the provided values in the above defined formula to determine the 95% confidence interval for the difference between the early eaters and late eaters in terms of consumption of carbohydrates. So,
Interpretation: Therefore, the 95% confidence interval for the difference between the means is obtained as
To explain: The comparison of information from obtained confidence interval with the information given by the significance test.
Answer to Problem 72E
Solution: The information provided by both confidence interval and the significance test shows that there is no significant difference between the two means of carbohydrates.
Explanation of Solution
The obtained confidence interval
To explain: A short summary on the results of the performed significance test and obtained confidence intervals for three dietary compositions.
Answer to Problem 72E
Solution: From the calculated value of the test statistic from the previous exercise for the consumption of fats, the null hypothesis is not rejected and it is concluded that there is no significant difference between the consumption of fats. The obtained confidence interval
Explanation of Solution
From the calculated value of the test statistic for the consumption of proteins, the null hypothesis is rejected and it is concluded that there is a significant difference between the consumption of proteins. The obtained confidence interval
From the calculated value of the test statistic for the consumption of carbohydrates, the null hypothesis is not rejected and it is concluded that there is no significant difference between the consumption of carbohydrates. The obtained confidence interval
Want to see more full solutions like this?
Chapter 7 Solutions
Introduction to the Practice of Statistics
- Problem 4. Margrabe formula and the Greeks (20 pts) In the homework, we determined the Margrabe formula for the price of an option allowing you to swap an x-stock for a y-stock at time T. For stocks with initial values xo, yo, common volatility σ and correlation p, the formula was given by Fo=yo (d+)-x0Þ(d_), where In (±² Ꭲ d+ õ√T and σ = σ√√√2(1 - p). дго (a) We want to determine a "Greek" for ỡ on the option: find a formula for θα (b) Is дго θα positive or negative? (c) We consider a situation in which the correlation p between the two stocks increases: what can you say about the price Fo? (d) Assume that yo< xo and p = 1. What is the price of the option?arrow_forwardWe consider a 4-dimensional stock price model given (under P) by dẴ₁ = µ· Xt dt + йt · ΣdŴt where (W) is an n-dimensional Brownian motion, π = (0.02, 0.01, -0.02, 0.05), 0.2 0 0 0 0.3 0.4 0 0 Σ= -0.1 -4a За 0 0.2 0.4 -0.1 0.2) and a E R. We assume that ☑0 = (1, 1, 1, 1) and that the interest rate on the market is r = 0.02. (a) Give a condition on a that would make stock #3 be the one with largest volatility. (b) Find the diversification coefficient for this portfolio as a function of a. (c) Determine the maximum diversification coefficient d that you could reach by varying the value of a? 2arrow_forwardQuestion 1. Your manager asks you to explain why the Black-Scholes model may be inappro- priate for pricing options in practice. Give one reason that would substantiate this claim? Question 2. We consider stock #1 and stock #2 in the model of Problem 2. Your manager asks you to pick only one of them to invest in based on the model provided. Which one do you choose and why ? Question 3. Let (St) to be an asset modeled by the Black-Scholes SDE. Let Ft be the price at time t of a European put with maturity T and strike price K. Then, the discounted option price process (ert Ft) t20 is a martingale. True or False? (Explain your answer.) Question 4. You are considering pricing an American put option using a Black-Scholes model for the underlying stock. An explicit formula for the price doesn't exist. In just a few words (no more than 2 sentences), explain how you would proceed to price it. Question 5. We model a short rate with a Ho-Lee model drt = ln(1+t) dt +2dWt. Then the interest rate…arrow_forward
- In this problem, we consider a Brownian motion (W+) t≥0. We consider a stock model (St)t>0 given (under the measure P) by d.St 0.03 St dt + 0.2 St dwt, with So 2. We assume that the interest rate is r = 0.06. The purpose of this problem is to price an option on this stock (which we name cubic put). This option is European-type, with maturity 3 months (i.e. T = 0.25 years), and payoff given by F = (8-5)+ (a) Write the Stochastic Differential Equation satisfied by (St) under the risk-neutral measure Q. (You don't need to prove it, simply give the answer.) (b) Give the price of a regular European put on (St) with maturity 3 months and strike K = 2. (c) Let X = S. Find the Stochastic Differential Equation satisfied by the process (Xt) under the measure Q. (d) Find an explicit expression for X₁ = S3 under measure Q. (e) Using the results above, find the price of the cubic put option mentioned above. (f) Is the price in (e) the same as in question (b)? (Explain why.)arrow_forwardThe managing director of a consulting group has the accompanying monthly data on total overhead costs and professional labor hours to bill to clients. Complete parts a through c. Question content area bottom Part 1 a. Develop a simple linear regression model between billable hours and overhead costs. Overhead Costsequals=212495.2212495.2plus+left parenthesis 42.4857 right parenthesis42.485742.4857times×Billable Hours (Round the constant to one decimal place as needed. Round the coefficient to four decimal places as needed. Do not include the $ symbol in your answers.) Part 2 b. Interpret the coefficients of your regression model. Specifically, what does the fixed component of the model mean to the consulting firm? Interpret the fixed term, b 0b0, if appropriate. Choose the correct answer below. A. The value of b 0b0 is the predicted billable hours for an overhead cost of 0 dollars. B. It is not appropriate to interpret b 0b0, because its value…arrow_forwardUsing the accompanying Home Market Value data and associated regression line, Market ValueMarket Valueequals=$28,416+$37.066×Square Feet, compute the errors associated with each observation using the formula e Subscript ieiequals=Upper Y Subscript iYiminus−ModifyingAbove Upper Y with caret Subscript iYi and construct a frequency distribution and histogram. LOADING... Click the icon to view the Home Market Value data. Question content area bottom Part 1 Construct a frequency distribution of the errors, e Subscript iei. (Type whole numbers.) Error Frequency minus−15 comma 00015,000less than< e Subscript iei less than or equals≤minus−10 comma 00010,000 0 minus−10 comma 00010,000less than< e Subscript iei less than or equals≤minus−50005000 5 minus−50005000less than< e Subscript iei less than or equals≤0 21 0less than< e Subscript iei less than or equals≤50005000 9…arrow_forward
- The managing director of a consulting group has the accompanying monthly data on total overhead costs and professional labor hours to bill to clients. Complete parts a through c Overhead Costs Billable Hours345000 3000385000 4000410000 5000462000 6000530000 7000545000 8000arrow_forwardUsing the accompanying Home Market Value data and associated regression line, Market ValueMarket Valueequals=$28,416plus+$37.066×Square Feet, compute the errors associated with each observation using the formula e Subscript ieiequals=Upper Y Subscript iYiminus−ModifyingAbove Upper Y with caret Subscript iYi and construct a frequency distribution and histogram. Square Feet Market Value1813 911001916 1043001842 934001814 909001836 1020002030 1085001731 877001852 960001793 893001665 884001852 1009001619 967001690 876002370 1139002373 1131001666 875002122 1161001619 946001729 863001667 871001522 833001484 798001589 814001600 871001484 825001483 787001522 877001703 942001485 820001468 881001519 882001518 885001483 765001522 844001668 909001587 810001782 912001483 812001519 1007001522 872001684 966001581 86200arrow_forwarda. Find the value of A.b. Find pX(x) and py(y).c. Find pX|y(x|y) and py|X(y|x)d. Are x and y independent? Why or why not?arrow_forward
- The PDF of an amplitude X of a Gaussian signal x(t) is given by:arrow_forwardThe PDF of a random variable X is given by the equation in the picture.arrow_forwardFor a binary asymmetric channel with Py|X(0|1) = 0.1 and Py|X(1|0) = 0.2; PX(0) = 0.4 isthe probability of a bit of “0” being transmitted. X is the transmitted digit, and Y is the received digit.a. Find the values of Py(0) and Py(1).b. What is the probability that only 0s will be received for a sequence of 10 digits transmitted?c. What is the probability that 8 1s and 2 0s will be received for the same sequence of 10 digits?d. What is the probability that at least 5 0s will be received for the same sequence of 10 digits?arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





