Chapter 7.10, Problem 43SEP

A Charpy V-notch specimen is tested by the impact-testing machine in Figure 7.9. In the test, the 10 kg hammer of arm-length 110 cm (measured from the fulcrum to the point of impact) is raised to 80° and then released. (a) What is the potential energy stored in the mass at this point? (b) After fracture of the specimen, the hammer swings to 45°. What is the potential energy at this point? (c) How much energy was expended in the fracture of the specimen? Hint: potential energy = mass × g × height.

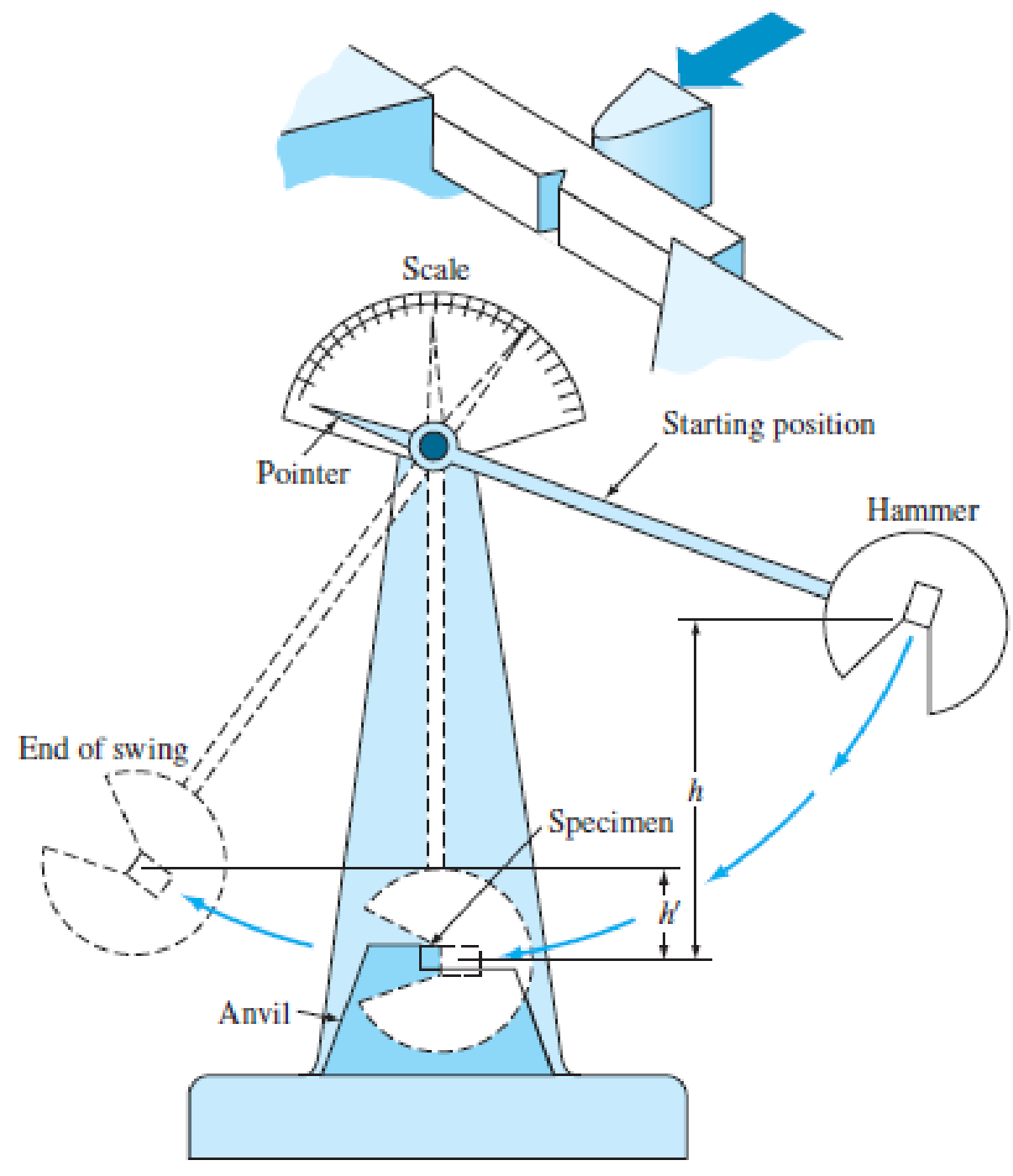
Figure 7.9

Schematic drawing of a standard impact-testing apparatus.

To determine

The potential energy stored in the mass at the point of impact when the hammer raised to $80°$.

Answer to Problem 43SEP

The potential energy stored in the mass at the point of impact is $176.58\text{Joule}$.

Explanation of Solution

Write the expression for Potential energy stored in the hammer is,

    $P.E_1=m\times g\times h_1$                                                                            (I)

Here, mass of hammer is $m$, acceleration due to gravity is $g$ and the height of impact is $h_1$.

Conclusion:

Below figure represent the new position of the hammer when hammer is raised to $90°$,

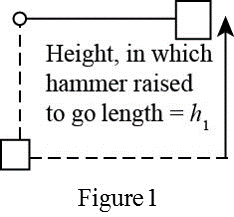
From Figure-1, when the hammer is rotated to an angle of $90°$, then the arm will become horizontal. From this we get height in which hammer raised $h_1$ height of length of the arm $l$.

Substitute $\text{15}\text{kg}$ for $\text{m}$, $9.81\text{m}/{\text{s}}^{\text{2}}$ for $g$ and $1.2\text{m}$ for $h_1$ in Equation (I)

    $\begin{array}{c}P.E_1=15\left(\text{kg}\right)\times 9.81\left(\text{m}/{\text{s}}^{\text{2}}\right)\times 120\left(\text{cm}\right)\\ =\left(17658\text{kg}\cdot \text{m}/{\text{s}}^{\text{2}}\right)\left(1\text{cm}\right)\left[\frac{1\text{m}}{100\text{cm}}\right]\\ =\left(176.58\text{kg}\cdot {\text{m}}^2/{\text{s}}^{\text{2}}\right)\left[\frac{1\text{N}}{1\text{kg}\cdot \text{m}/{\text{s}}^{\text{2}}}\right]\left[\frac{1\text{J}}{1\text{N}\cdot \text{m}}\right]\\ =\text{176}\text{.58}\text{J}\end{array}$

Thus, the potential energy stored in the mass at the point of impact is $176.58\text{J}$.

To determine

The potential energy at the point of impact when the hammer swing to $45°$.

Answer to Problem 43SEP

The potential energy stored in the mass at the point of impact is $51.73\text{J}$.

Explanation of Solution

Write the expression height of impact when hammer is raised $45°$.

    $h_2=l-l\cos 45°$                                                                        (II).

Here, height of impact is $h_2$ when hammer raised $45°$ and length of the arm is $l$.

Write the expression for Potential energy stored in the hammer is,

    $P.E_2=m\times g\times h_2$                                                                       (III)

Here, mass of hammer is $m$, acceleration due to gravity is $g$ and height of impact is $h_1$.

Conclusion:

Below figure represent the new position of the hammer when hammer is swing to $45°$,

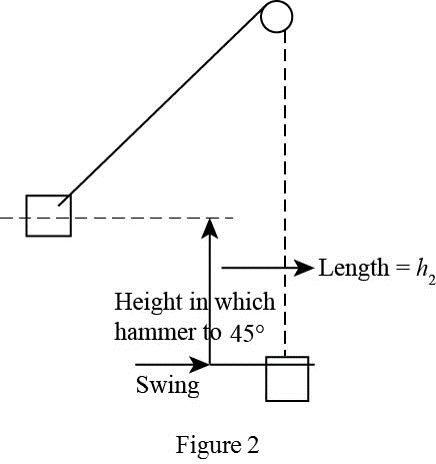
From Figure-2, when the hammer is swing to an angle of $45°$, then the arm will become horizontal. From this we get height in which hammer raised $h_2$ height of length of the arm $l$.

Substitute $12\text{cm}$ for $l$ in Equation (II).

    $\begin{array}{c}{h}_2=\left(120\text{cm}\right)-\left(120\text{cm}\right)\times \cos 45°\\ =35.16\left(\text{cm}\right)\left(\frac{1\text{m}}{100\text{cm}}\right)\\ =0.3516\text{m}\end{array}$

Substitute $\text{15}\text{kg}$ for $\text{m}$, $9.81\text{m}/{\text{s}}^{\text{2}}$ for $g$ and $0.3516\text{m}$ for $h_2$ in equation (III).

    $\begin{array}{c}P.E_2=15\left(\text{kg}\right)\times 9.81\left(\text{m}/{\text{s}}^{\text{2}}\right)\times 0.3516\left(\text{m}\right)\\ =\left(51.73\text{kg}\cdot {\text{m}}^2/{\text{s}}^{\text{2}}\right)\left[\frac{1\text{N}}{1\text{kg}\cdot \text{m}/{\text{s}}^{\text{2}}}\right]\left[\frac{1\text{J}}{1\text{N}\cdot \text{m}}\right]\\ \text{=51}\text{.73}\text{J}\end{array}$

Thus, the potential energy stored in the mass at the point of impact is $51.73\text{J}$.

To determine

The amount of energy expended in the fracture of the specimen.

Answer to Problem 43SEP

The amount of energy expended in the fracture of the specimen is $124.85\text{J}$.

Explanation of Solution

Write the expression of energy expended in the fracture of the specimen is,

    $E=P.E_1-P.E_2$                                                              (IV).

Conclusion:

Substitute $176.58\text{Joule}$ for $P.E_1$ and $51.73\text{Joule}$ for $P.E_2$ in Equation (IV).

    $\begin{array}{c}E=176.58\text{J}-51.73\text{J}\\ =124.85\text{J}\end{array}$

The amount of energy expended in the fracture of the specimen is $124.85\text{J}$.