
Concept explainers
Light Energy, and the Hydrogen Atom
- a Which has the greater wavelength, blue light or red light?
- b How do the
frequencies of blue light and red light compare? - c How does the energy of blue light compare with that of red light?
- d Does blue light have a greater
speed than red light ?- e How does the energy of three photons from a blue light source compare with the energy of one photon of blue light from the same source? How does the energy of two photons corresponding to a wavelength of 451 nm (blue light) compare with the energy of three photons corresponding to a wavelength of 704 nm (red light)?
- f A hydrogen atom with an electron in its ground state interacts with a photon of light with a wavelength of 1.22 × 10−6 m. Could the electron make a transition from the ground state to a higher energy level? If it does make a transition, indicate which one. If no transition can occur, explain.
- g If you have one mole of hydrogen atoms with their electrons in the n = 1 level, what is the minimum number of photons you would need to interact with these atoms in order to have all of their electrons promoted to the n = 3 level? What
wavelength of light would you need to perform this experiment?
(a)
Interpretation:
The light with higher wavelength has to be identified from the given lights.
Concept introduction:
Relation between frequency and wavelength is,
C is the speed of light.
h is Planck’s constant (
E is energy of light particle.
Wavelength and frequency are inversely proportional to each other.
The distance between any two similar points of a wave is called wavelength
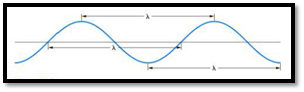
Figure 1
Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.
Answer to Problem 7.23QP
Red light has larger wavelength than blue light.
Explanation of Solution
To identify: The light with higher wavelength.
Wavelength and frequency are inversely proportional to each other. Frequency of blue light is higher than red light. Thus, red light has larger wavelength than blue light.
By using the relation between wavelength and frequency, the light with higher wavelength was identified.
(b)
Interpretation:
The light with higher frequency has to be identified from the given lights.
Concept introduction:
Relation between frequency and wavelength is,
C is the speed of light.
h is Planck’s constant (
E is energy of light particle.
Wavelength and frequency are inversely proportional to each other.
The distance between any two similar points of a wave is called wavelength
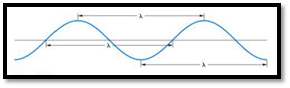
Figure 1
Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.
Answer to Problem 7.23QP
Blue light has larger frequency than red light.
Explanation of Solution
To identify: The light with higher frequency.
Wavelength and frequency are inversely proportional to each other. Wavelength of blue light is less than red light. Thus, blue light has larger frequency than red light.
By using the relation between wavelength and frequency, the light with higher frequency was identified.
(c)
Interpretation:
The energies of blue light and red light has to be related.
Concept introduction:
Relation between frequency and wavelength is,
C is the speed of light.
h is Planck’s constant (
E is energy of light particle.
Wavelength and frequency are inversely proportional to each other.
The distance between any two similar points of a wave is called wavelength

Figure 1
Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.
Answer to Problem 7.23QP
Blue light has higher energy than red light.
Explanation of Solution
To compare: The energy of blue light and red light.
Energy and frequency are directly proportional to each other. Frequency of blue light is higher than red light. Thus, blue light has higher energy than red light.
By using the relation between wavelength and frequency, the energy of blue light and red light was related.
(d)
Interpretation:
The speed of blue light and red light has to be compared.
Concept introduction:
Relation between frequency and wavelength is,
C is the speed of light.
h is Planck’s constant (
E is energy of light particle.
Wavelength and frequency are inversely proportional to each other.
The distance between any two similar points of a wave is called wavelength
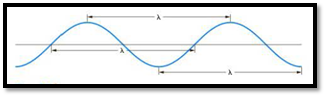
Figure 1
Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.
Answer to Problem 7.23QP
Blue light has higher energy than red light.
Explanation of Solution
To compare: The speed of blue light and red light.
Energy and frequency are directly proportional to each other. Frequency of blue light is higher than red light. Thus, blue light has higher energy than red light.
By using the relation between wavelength and frequency, the energy of blue light and red light was related.
(e)
Interpretation:
The energy of one photon and energy of three photons of blue light has to be compared.
Concept introduction:
Relation between frequency and wavelength is,
C is the speed of light.
h is Planck’s constant (
E is energy of light particle.
Wavelength and frequency are inversely proportional to each other.
The distance between any two similar points of a wave is called wavelength
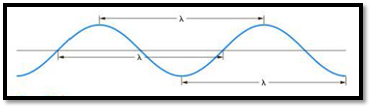
Figure 1
Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.
Answer to Problem 7.23QP
Blue light (
Explanation of Solution
To compare: The energy of one photon and energy of three photons of blue light.
Blue light with energy of three photons is thrice the energy of one photon. In order to relate the energy of two photon (blue light) with energy of three photon (red light), the energy is given as
Blue light (
By using the relation between wavelength and frequency, the energy of two photon of blue light and energy of three photons of red light was related.
(f)
Interpretation:
The possibility of transition of an electron of hydrogen atom from ground state to higher energy state has to be determined.
Concept introduction:
Relation between frequency and wavelength is,
C is the speed of light.
h is Planck’s constant (
E is energy of light particle.
Wavelength and frequency are inversely proportional to each other.
The distance between any two similar points of a wave is called wavelength
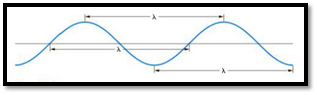
Figure 1
Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.
Bohr developed a rule for quantization of energy that could be applicable to the electron of an atom in motion. By using this he derived a formula for energy levels of electron in H-atom.
Answer to Problem 7.23QP
The obtained energy for transition is greater than the energy of light. Therefore, no transition occurs.
Explanation of Solution
To determine: The possibility of transition of an electron of hydrogen atom from ground state to higher energy state.
By using the below formula and calculate frequency and energy of light
The minimum energy required for the transition of
The obtained energy for transition is greater than the energy of light. Therefore, no transition occurs.
The possibility of transition of an electron of hydrogen atom from ground state to higher energy state was determined.
(g)
Interpretation:
The energy required for transition of an electron of hydrogen atom from
Concept introduction:
Relation between frequency and wavelength is,
C is the speed of light.
h is Planck’s constant (
E is energy of light particle.
Wavelength and frequency are inversely proportional to each other.
The distance between any two similar points of a wave is called wavelength
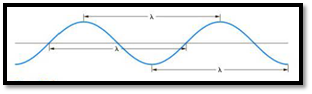
Figure 1
Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.
Bohr developed a rule for quantization of energy that could be applicable to the electron of an atom in motion. By using this he derived a formula for energy levels of electron in H-atom.
Answer to Problem 7.23QP
The minimum energy required for the transition of
The wavelength of the light is
Explanation of Solution
To determine: The energy required for transition of an electron of hydrogen atom from
The minimum energy required for the transition of
The energy required for transition of an electron of hydrogen atom from
Want to see more full solutions like this?
Chapter 7 Solutions
Bundle: General Chemistry, Loose-leaf Version, 11th + OWLv2, 4 terms (24 months) Printed Access Card
- Curved arrows are used to illustrate the flow of electrons. Using the provided starting and product structures, draw the curved electrons-pushing arrows for the following reaction or mechanistic step(s).arrow_forwardWhat is the IUPAC name of the following compound? CH₂CH₂ H CI H₂CH₂C H CH₂ Selected Answer: O (35,4R)-4 chloro-3-ethylpentane Correctarrow_forwardCurved arrows are used to illustrate the flow of electrons. Using the provided starting and product structures, draw the curved electrons-pushing arrows for the following reaction or mechanistic step(s).arrow_forward
- Curved arrows are used to illustrate the flow of electrons. Using the provided starting and product structures, draw the curved electron-pushing arrows for the following reaction or mechanistic step(s). Be sure to account for all bond-breaking and bond-making steps. I I I H Select to Add Arrows HCI, CH3CH2OHarrow_forwardCurved arrows are used to illustrate the flow of electrons. Use the reaction conditions provided and the follow the arrows to draw the intermediate and product in this reaction or mechanistic step(s).arrow_forwardCurved arrows are used to illustrate the flow of electrons. Use the reaction conditions provided and follow the curved arrows to draw the intermediates and product of the following reaction or mechanistic step(s).arrow_forward
- Curved arrows are used to illustrate the flow of electrons. Use the reaction conditions provided and follow the arrows to draw the intermediate and the product in this reaction or mechanistic step(s).arrow_forwardLook at the following pairs of structures carefully to identify them as representing a) completely different compounds, b) compounds that are structural isomers of each other, c) compounds that are geometric isomers of each other, d) conformers of the same compound (part of structure rotated around a single bond) or e) the same structure.arrow_forwardGiven 10.0 g of NaOH, what volume of a 0.100 M solution of H2SO4 would be required to exactly react all the NaOH?arrow_forward
- 3.50 g of Li are combined with 3.50 g of N2. What is the maximum mass of Li3N that can be produced? 6 Li + N2 ---> 2 Li3Narrow_forward3.50 g of Li are combined with 3.50 g of N2. What is the maximum mass of Li3N that can be produced? 6 Li + N2 ---> 2 Li3Narrow_forwardConcentration Trial1 Concentration of iodide solution (mA) 255.8 Concentration of thiosulfate solution (mM) 47.0 Concentration of hydrogen peroxide solution (mM) 110.1 Temperature of iodide solution ('C) 25.0 Volume of iodide solution (1) used (mL) 10.0 Volume of thiosulfate solution (5:03) used (mL) Volume of DI water used (mL) Volume of hydrogen peroxide solution (H₂O₂) used (mL) 1.0 2.5 7.5 Time (s) 16.9 Dark blue Observations Initial concentration of iodide in reaction (mA) Initial concentration of thiosulfate in reaction (mA) Initial concentration of hydrogen peroxide in reaction (mA) Initial Rate (mA's)arrow_forward
 World of Chemistry, 3rd editionChemistryISBN:9781133109655Author:Steven S. Zumdahl, Susan L. Zumdahl, Donald J. DeCostePublisher:Brooks / Cole / Cengage LearningChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co
World of Chemistry, 3rd editionChemistryISBN:9781133109655Author:Steven S. Zumdahl, Susan L. Zumdahl, Donald J. DeCostePublisher:Brooks / Cole / Cengage LearningChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co
 Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning Introductory Chemistry: An Active Learning Approa...ChemistryISBN:9781305079250Author:Mark S. Cracolice, Ed PetersPublisher:Cengage Learning
Introductory Chemistry: An Active Learning Approa...ChemistryISBN:9781305079250Author:Mark S. Cracolice, Ed PetersPublisher:Cengage Learning Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning





