Chapter 7, Problem 70E

(a)

To determine

Calculate the energy stored in each energy storage element.

Answer to Problem 70E

The value of energy stored in the inductor $\left(w_L\right)$ is $30.3\text{J}$ and capacitor $\left(w_C\right)$ is $2\text{J}$.

Explanation of Solution

Given data:

Refer to Figure 7.84 in the textbook.

Calculation:

The given circuit is redrawn as shown in Figure 1.

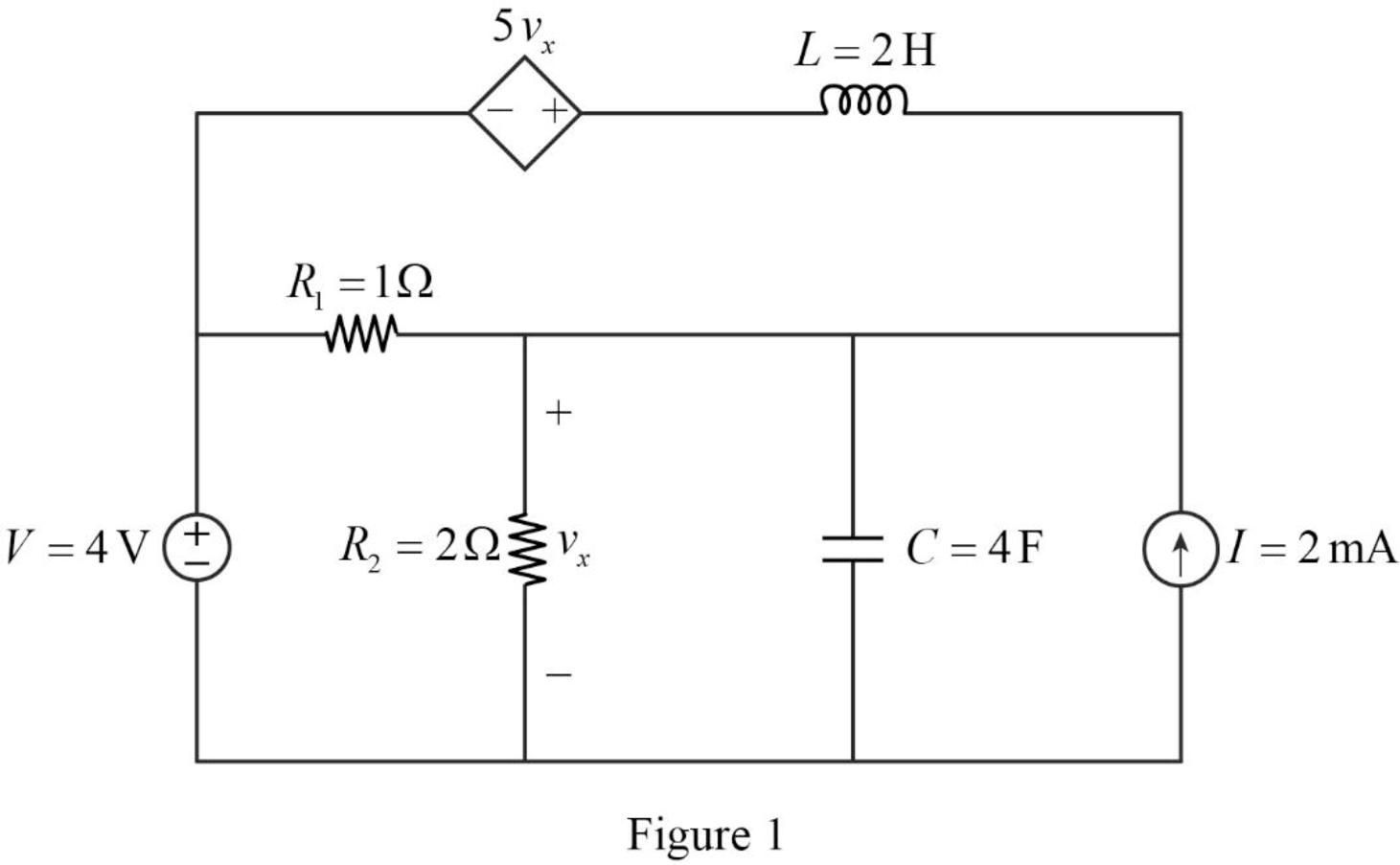
For a DC circuit, at steady state condition, the capacitor acts like open circuit and the inductor acts like short circuit.

Now, the Figure 1 is reduced as shown in Figure 2.

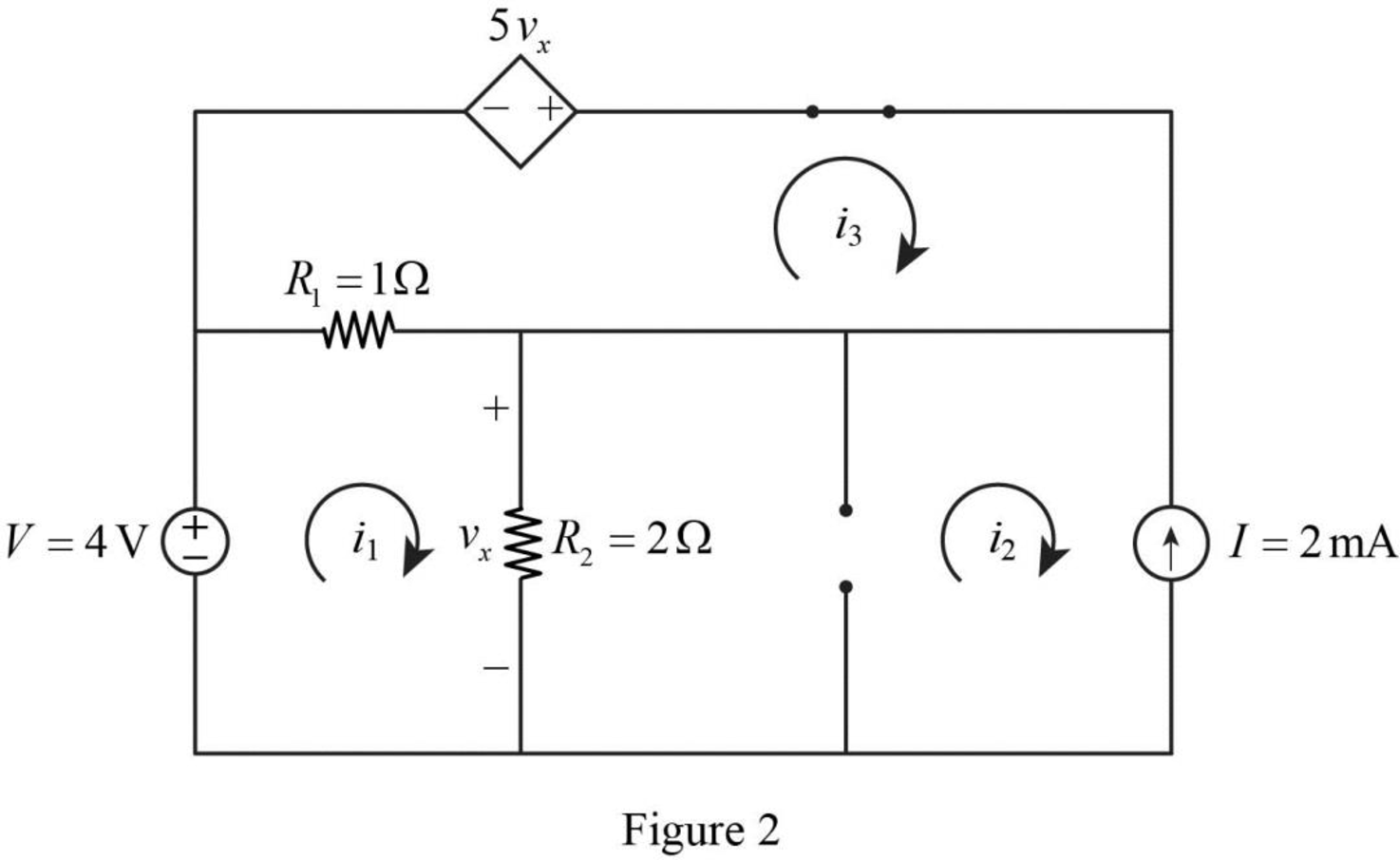
Apply Kirchhoff’s voltage law for loop 1 in Figure 2.

$\begin{array}{l}-4+1\left(i_1-i_3\right)+2\left(i_1-i_2\right)=0\\ -4+i_1-i_3+2i_1-2i_2=0\end{array}$

$3i_1-2i_2-i_3=4$        (1)

Refer to Figure 2, the current $2\text{mA}$ flows through loop 2 in opposite direction. Therefore, the value of current $i_2$ is calculated as follows:

$\begin{array}{c}{i}_2=-2\text{mA}\\ =-2\times {10}^{-3}\text{A}\left\{\because 1\text{m}={10}^{-3}\right\}\\ =-0.002\text{A}\end{array}$

Substitute $-0.002\text{A}$ for $i_2$ in equation (1).

$\begin{array}{l}3i_1-2\left(-0.002\right)-i_3=4\\ 3i_1+0.004-i_3=4\\ 3i_1-i_3=4-0.004\\ 3i_1-i_3=3.996\end{array}$

Simplify the above equation to find $i_3$.

$i_3=3i_1-3.996$        (2)

Apply Kirchhoff’s voltage law for loop 3 in Figure 2.

$-5v_x+1\left(i_3-i_1\right)=0$

$-5v_x+i_3-i_1=0$        (3)

Refer to Figure 2, the voltage across the resistor $R_2$ is mentioned as $v_x$.

The voltage $v_x$ is calculated as follows:

$v_x=2\left(i_1-i_2\right)$        (4)

Substitute equation (4) in (3).

$\begin{array}{l}-5\left(2\left(i_1-i_2\right)\right)+i_3-i_1=0\\ -10i_1+10i_2+i_3-i_1=0\\ -11i_1+10i_2+i_3=0\end{array}$

Substitute $-0.002\text{A}$ for $i_2$ in above equation.

$\begin{array}{l}-11i_1+10\left(-0.002\right)+i_3=0\\ -11i_1-0.02+i_3=0\end{array}$

$-11i_1+i_3=0.02$        (5)

Substitute equation (2) in (5).

$\begin{array}{l}-11i_1+3i_1-3.996=0.02\\ -8i_1=3.996+0.02\\ -8i_1=4.016\end{array}$

Simplify the above equation to find $i_1$.

$\begin{array}{c}{i}_1=\frac{4.016}{\left(-8\right)}\\ =-0.502\text{A}\end{array}$

Substitute $-0.502\text{A}$ for $i_1$ in equation (2) to find $i_3$.

$\begin{array}{c}{i}_3=3\left(-0.502\right)-3.996\\ =-1.506-3.996\\ =-5.502\text{A}\end{array}$

Refer to Figure 2, the current $i_3$ is the current flows through the inductor.

$i_L=i_3=-5.502\text{A}$

Substitute $-0.502\text{A}$ for $i_1$, and $-0.002\text{A}$ for $i_2$ in equation (4) to find $v_x$.

$\begin{array}{c}{v}_x=\left(2\Omega \right)\left(-0.502\text{A}-\left(-0.002\text{A}\right)\right)\\ =\left(2\Omega \right)\left(-0.502\text{A+}0.002\text{A}\right)\\ =\left(2\Omega \right)\left(-0.5\text{A}\right)\\ =-1\text{V}\end{array}$

Refer to Figure 2, the resistor $R_2$ and capacitor $\left(C\right)$ is connected in parallel. For the parallel connection, the voltage is same. Therefore, the voltage across the capacitor is equal to voltage across the resistor $R_2$.

$v_C=v_x=-1\text{V}$

Write a general expression to calculate the energy stored in a inductor.

$w_L=\frac{1}{2}L{i}_L^2$        (6)

Here,

$L$ is the value of inductance, and

$i_L$ is the current flows through inductor.

Write a general expression to calculate the energy stored in a capacitor.

$w_C=\frac{1}{2}C{v}_x^2$        (7)

Here,

$C$ is the value of capacitance, and

$v_C$ is the voltage across the capacitor.

Substitute $-5.502\text{A}$ for $i_L$, and $2\text{H}$ for $L$ equation (6) to find $w_L$.

$\begin{array}{c}{w}_L=\frac{1}{2}\left(2\text{H}\right){\left(-5.502\text{A}\right)}^2\\ =\frac{1}{2}\left(2\text{H}\right)\left(30.3{\text{A}}^2\right)\\ =\frac{1}{2}\left(2\Omega \cdot \text{s}\right)\left(30.3\frac{{\text{C}}^2}{{\text{s}}^2}\right)\left\{\begin{array}{l}\because 1\text{H}=1\Omega \cdot 1\text{s}\\ \text{1}\text{A}=\frac{1\text{C}}{1\text{s}}\end{array}\right\}\end{array}$

Simplify the above equation to find $w_L$.

$\begin{array}{c}{w}_L=30.3\frac{{\text{C}}^2\cdot \left(\frac{\text{V}}{\text{A}}\right)}{\text{s}}\left\{\because 1\Omega =\frac{\text{1}\text{V}}{\text{1}\text{A}}\right\}\\ =30.3\frac{{\text{C}}^2\cdot \text{V}}{\frac{\text{C}}{\text{s}}\cdot \text{s}}\left\{\because \text{1}\text{A}=\frac{1\text{C}}{1\text{s}}\right\}\\ =30.3\text{C}\cdot \text{V}\\ =30.3\text{J}\left\{\because 1\text{J}=1\text{C}\cdot \text{1}\text{V}\right\}\end{array}$

Substitute $4\text{F}$ for $C$ and $-1\text{V}$ for $v_C$ in equation (7) to find $w_C$.

$\begin{array}{c}{w}_C=\frac{1}{2}\left(4\text{F}\right){\left(-1\text{V}\right)}^2\\ =\frac{1}{2}\left(4\text{F}\right)\left(1{\text{V}}^2\right)\\ =2\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =2\left(\frac{\text{A}\cdot \text{s}}{\text{V}}\cdot {\text{V}}^2\right)\left\{\because 1\text{F}=\frac{\text{1}\text{A}\cdot 1\text{s}}{\text{1}\text{V}}\right\}\end{array}$

Simplify the above equation to find $w_C$.

$\begin{array}{c}{w}_C=2\left(\text{A}\cdot \text{s}\cdot \text{V}\right)\\ =2\left(\frac{\text{C}}{\text{s}}\cdot \text{s}\cdot \text{V}\right)\left\{\because 1\text{A}=\frac{1\text{C}}{1\text{s}}\right\}\\ =2\text{C}\cdot \text{V}\\ =2\text{J}\left\{\because 1\text{J}=1\text{C}\cdot 1\text{V}\right\}\end{array}$

Conclusion:

Thus, the value of energy stored in the inductor $\left(w_L\right)$ is $30.3\text{J}$ and capacitor $\left(w_C\right)$ is $2\text{J}$.

(b)

To determine

Verify the calculated answers with an appropriate simulation.

Explanation of Solution

Create the new schematic in LTspice and draw the Figure 1 as shown in Figure 3. Use the Label net option and write VR2 to find voltage across resistor $R_2$.

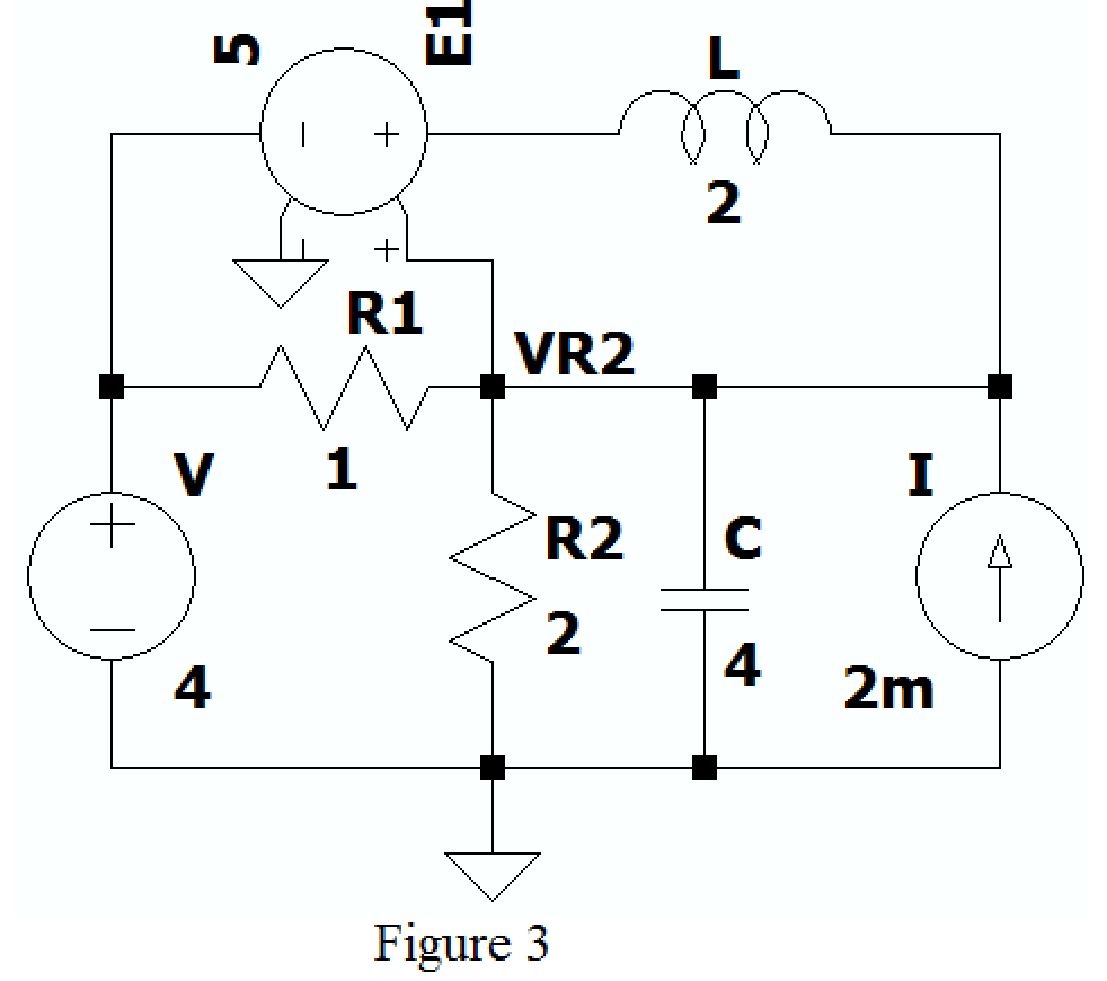
Choose the Dc op point in Edit simulation Cmd as shown in Figure 4.

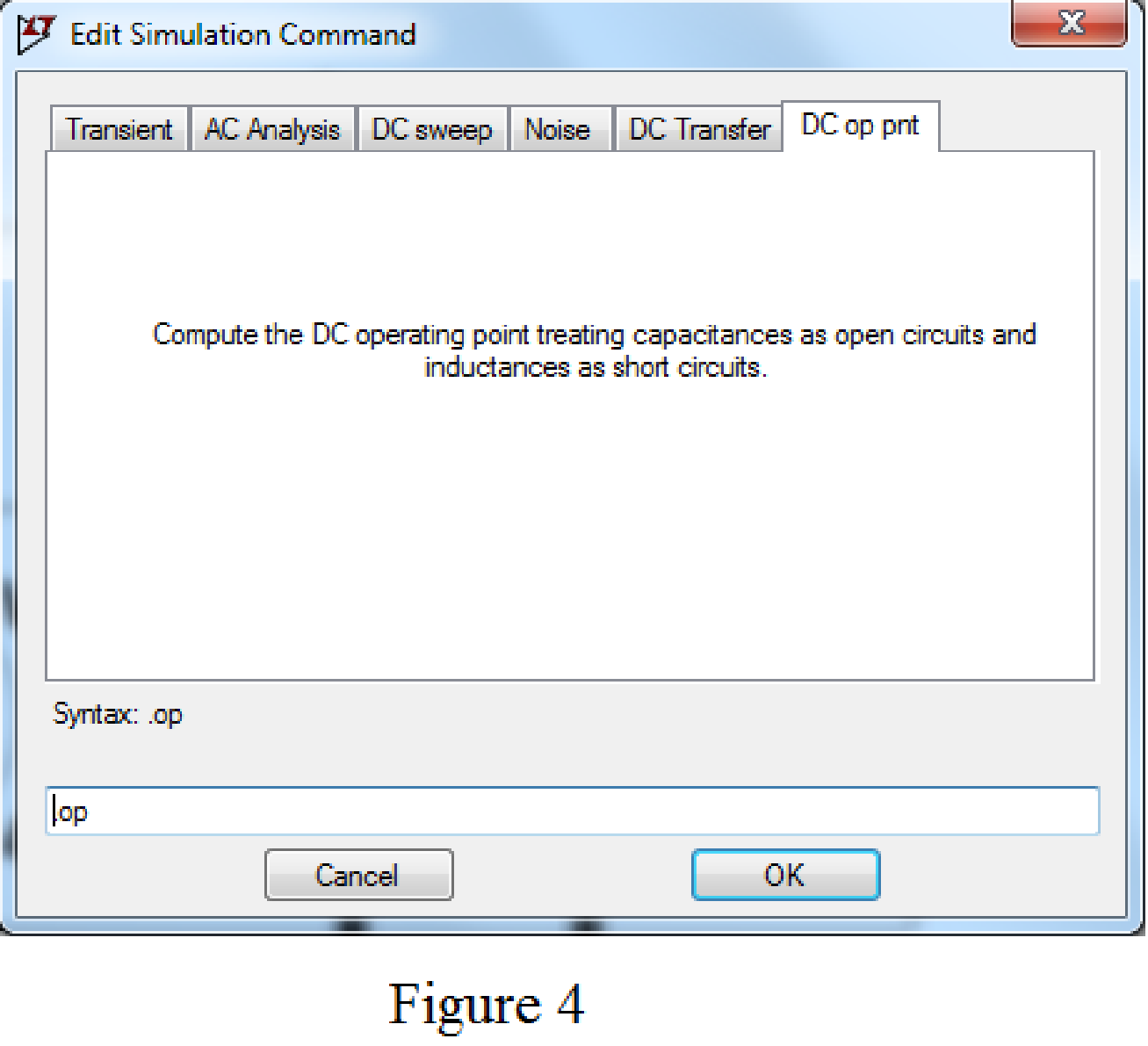
After adding the above mentioned commands the circuit becomes as shown in Figure 5.

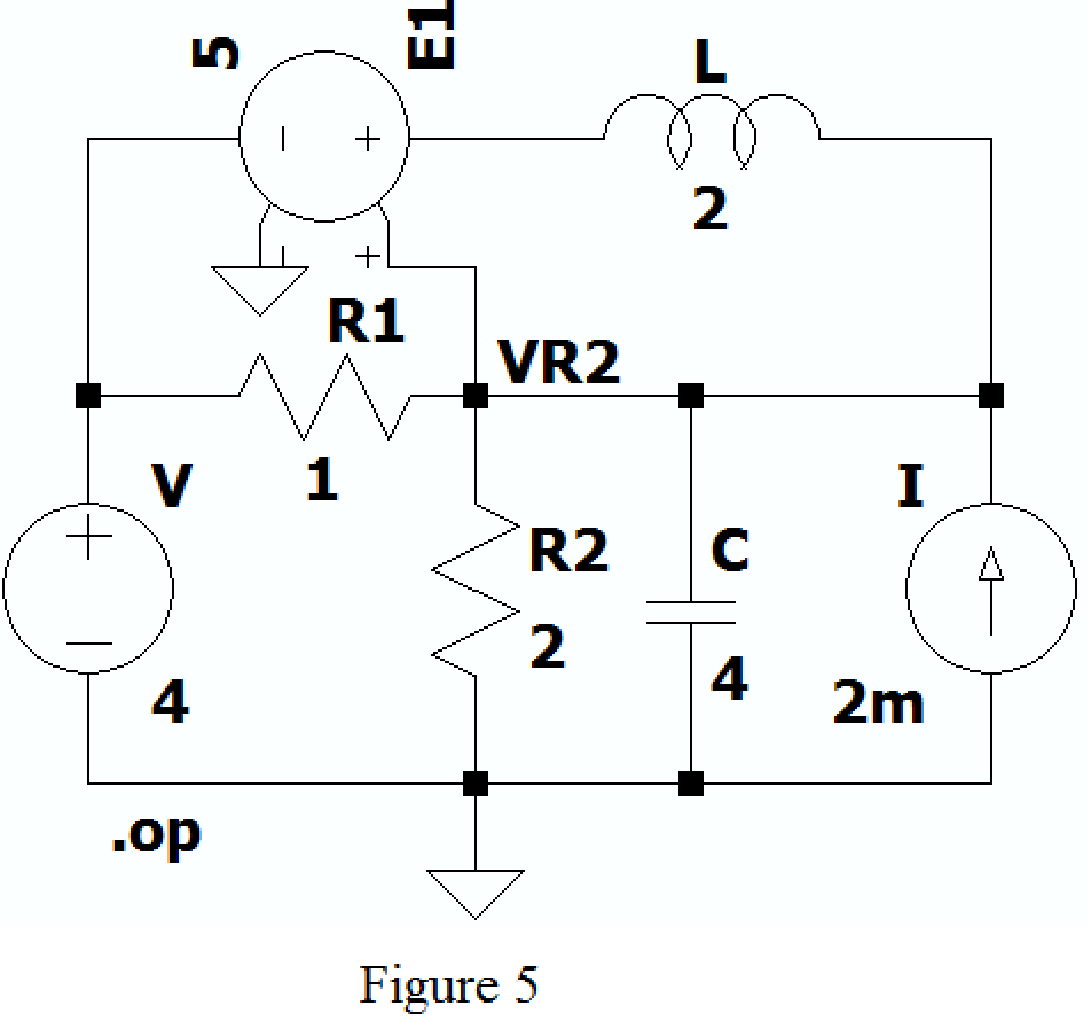
Now run the simulation, the table will be displayed with the values of current through resistors, capacitor and voltage across the capacitor as shown in Figure 6.

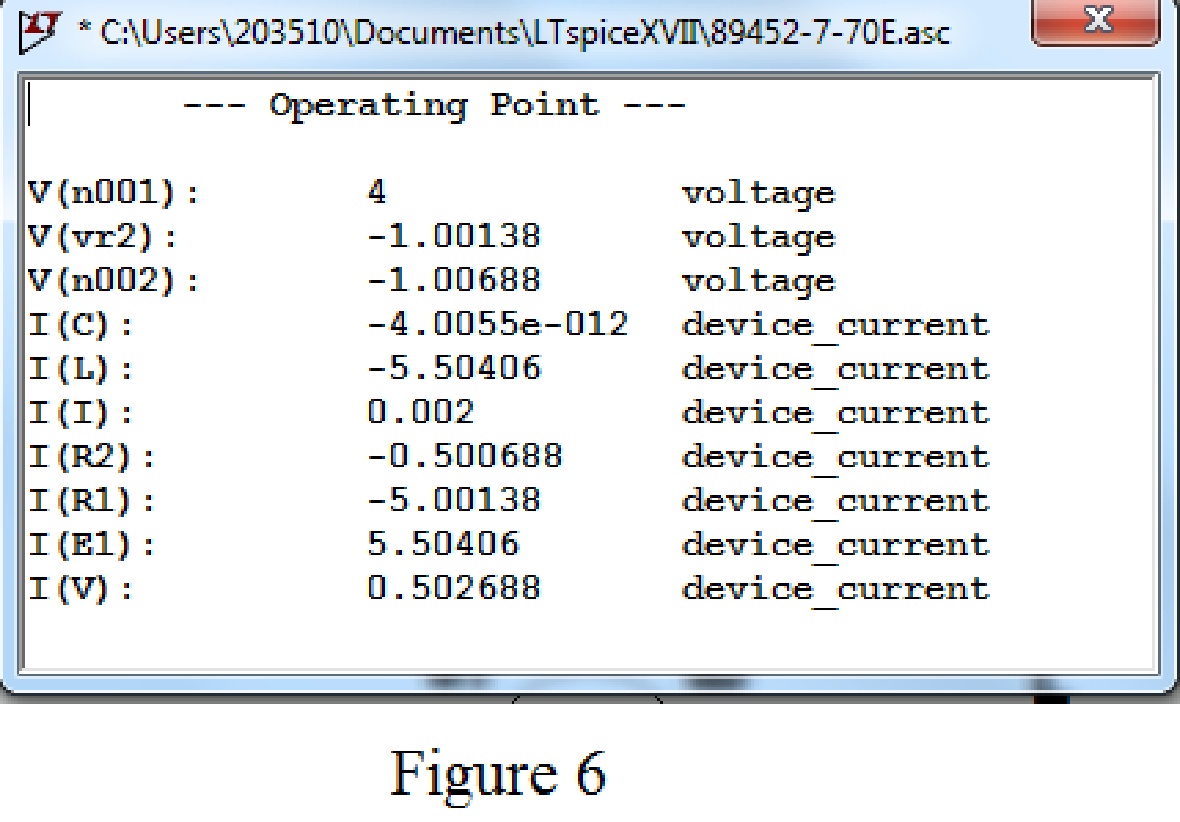
Refer to Figure 6, the value of voltage across the capacitor $\left(v_{R_2}\right)$ is $-1.00138\text{V}$ and the current through the inductor is $-5.50406\text{A}$.

Conclusion:

Thus, the calculated answers are verified with an appropriate SPICE simulation.