
Concept explainers
(a) Suppose a constant force acts on an object. The force does not vary with time or with the position or the velocity of the object. Start with the general definition for work done by a force
and show that the force is conservative. (b) As a special case, suppose the force
(a)
That the constant force act on the object is conservative.
Answer to Problem 32P
The constant force applied on the object is conservative in nature.
Explanation of Solution
The work done by a conservative force on a particle moving between any two points is independent of the path taken by the particle. Its only depends upon the end points of the path taken by the particle to move.
The general definition for work done by a force
Write the formula to calculate the work done by the force on the object
Here,
Since the force is constant that does not vary with respect to time or the position or the velocity of the object. So, the value of force can be taken out from the integration since it is constant quantity.
Now, here the force is constant so, the work done by this force on the object in only depends upon the end points of the displace object that shows the work done is independent of the path taken by the object to displace between the end points. But the work done is independent of the path only when the force is conservative.
Conclusion:
Therefore, the constant force applied on the object is conservative in nature.
(b)
The work done by the force
Answer to Problem 32P
The work done by the force
Explanation of Solution
The given force is
The force acting on the particle is
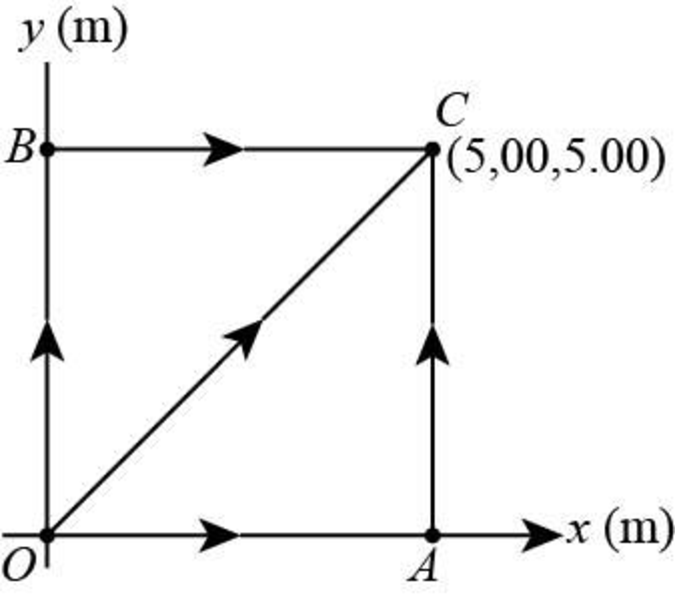
Figure (I)
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
In the path
Write the formula to calculate the work done by the force on the particle
Substitute
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the purple path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the red path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
The path
Taking the limits on integration,
Since the work done by the force
Conclusion:
Therefore, the work done by the force on the particle as it goes from O to C along the blue path is
(c)
Whether the work done by the force
Answer to Problem 32P
The work done by the force
Explanation of Solution
The force acting on the particle is
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the purple path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the red path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
The path
Taking the limits on integration,
Since the work done by the force
Conclusion:
Therefore, the work done by the force on the particle as it goes from O to C along the blue path is
(d)
Whether the work done by the force
Answer to Problem 32P
The work done by the force
Explanation of Solution
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Substitute
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the purple path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Substitute
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the red path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
The path
Substitute
Taking the limits on integration,
Conclusion:
Therefore, the work done by the force on the particle as it goes along the three paths is not same.
Want to see more full solutions like this?
Chapter 7 Solutions
Physics for Scientists and Engineers
- No chatgpt plsarrow_forwardCar A starts from rest at t = 0 and travels along a straight road with a constant acceleration of 6 ft/s^2 until it reaches a speed of 60ft/s. Afterwards it maintains the speed. Also, when t = 0, car B located 6000 ft down the road is traveling towards A at a constant speed of 80 ft/s. Determine the distance traveled by Car A when they pass each other.Write the solution using pen and draw the graph if needed.arrow_forwardIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B, will be 2 μF A 1 µF B 3 µFarrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed. NOT AI PLSarrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardPlease don't use Chatgpt will upvote and give handwritten solutionarrow_forward
- No chatgpt pls will upvote Already got wrong chatgpt answerarrow_forwardAn electron and a proton are each accelerated through a potential difference of 21.0 million volts. Find the momentum (in MeV/c) and the kinetic energy (in MeV) of each, and compare with the results of using the classical formulas. Momentum (MeV/c) relativistic classical electron proton Kinetic Energy (MeV)arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 20.0 µF.) (a) Find the equivalent capacitance between points a and b. µF (b) Calculate the charge on each capacitor, taking ΔVab = 14.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





