Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
6th Edition
ISBN: 9780321914620
Author: Jeffrey O. Bennett, William L. Briggs
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.A, Problem 39E
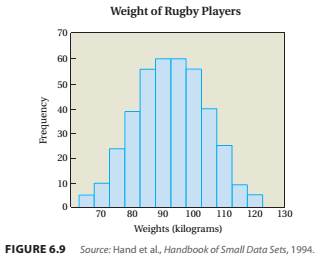
Smooth Distributions. Through each histogram, draw a smooth curve that captures its important features. Then classify the distribution according to its number of peaks, symmetry or skew-ness, and variation.
39. Weights of a sample of 391 rugby players, shown in Figure 6.9
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
9. The concentration function of a random variable X is defined as
Qx(h) = sup P(x ≤ X ≤x+h), h>0.
x
(a) Show that Qx+b (h) = Qx(h).
(b) Is it true that Qx(ah) =aQx(h)?
(c) Show that, if X and Y are independent random variables, then
Qx+y (h) min{Qx(h). Qy (h)).
To put the concept in perspective, if X1, X2, X, are independent, identically
distributed random variables, and S₁ = Z=1Xk, then there exists an absolute
constant, A, such that
A
Qs, (h) ≤
√n
Some references: [79, 80, 162, 222], and [204], Sect. 1.5.
29
Suppose that a mound-shaped data set has a
must mean of 10 and standard deviation of 2.
a. About what percentage of the data should
lie between 6 and 12?
b. About what percentage of the data should
lie between 4 and 6?
c. About what percentage of the data should
lie below 4?
91002 175/1
3
2,3,
ample
and
rical
t?
the
28 Suppose that a mound-shaped data set has a
mean of 10 and standard deviation of 2.
a. About what percentage of the data should
lie between 8 and 12?
b. About what percentage of the data should
lie above 10?
c. About what percentage of the data should
lie above 12?
Chapter 6 Solutions
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Ch. 6.A - Prob. 1QQCh. 6.A - On a math exam, one student scores 79 while 25...Ch. 6.A - One hundred students take a chemistry exam. All...Ch. 6.A - Twenty students take a political science exam....Ch. 6.A - A survey asks students to state many sodas they...Ch. 6.A - Among professional actors, a small number of...Ch. 6.A - The distribution of wages at a company is...Ch. 6.A - Compared to a distribution with a broad central...Ch. 6.A - Prob. 9QQCh. 6.A - The mayor of a town is considering a run for...
Ch. 6.A - 1. Define and distinguish among mean, median, and...Ch. 6.A - Prob. 2ECh. 6.A - Briefly describe at least two possible sources of...Ch. 6.A - Prob. 4ECh. 6.A - Prob. 5ECh. 6.A - Prob. 6ECh. 6.A - In my data set of 10 exam scores, the mean turned...Ch. 6.A - In my data set of 10 exam scores, the median...Ch. 6.A - I made a distribution of 15 apartment rents in my...Ch. 6.A - Prob. 10ECh. 6.A - The distribution of grades was left-skewed, but...Ch. 6.A - There’s much more variation in the ages of the...Ch. 6.A - Prob. 13ECh. 6.A - Mean, Median, and Mode. Compute the mean, median,...Ch. 6.A - Mean, Median, and Mode. Compute the mean, median,...Ch. 6.A - Prob. 16ECh. 6.A - 13–18: Mean, Median, and Mode. Compute the mean,...Ch. 6.A - Mean, Median, and Mode. Compute the mean, median,...Ch. 6.A - Outlier Coke. Cans of Coca-Cola vary slightly in...Ch. 6.A - Prob. 20ECh. 6.A - Prob. 21ECh. 6.A - Appropriate Average. State, with an explanation,...Ch. 6.A - Prob. 23ECh. 6.A - Appropriate Average. State, with an explanation,...Ch. 6.A - Prob. 25ECh. 6.A - Appropriate Average. State, with an explanation,...Ch. 6.A - Prob. 27ECh. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Prob. 33ECh. 6.A - Describing Distributions. Consider the following...Ch. 6.A - Prob. 35ECh. 6.A - Prob. 36ECh. 6.A - Smooth Distributions. Through each histogram, draw...Ch. 6.A - Smooth Distributions. Through each histogram, draw...Ch. 6.A - Smooth Distributions. Through each histogram, draw...Ch. 6.A - Prob. 40ECh. 6.A - Family Income. Suppose you study family income in...Ch. 6.A - Airline Delays. Suppose you are a scheduler for a...Ch. 6.A - Prob. 43ECh. 6.A - Prob. 44ECh. 6.A - Prob. 45ECh. 6.A - Prob. 46ECh. 6.A - Prob. 47ECh. 6.A - Prob. 48ECh. 6.A - Prob. 49ECh. 6.A - 50. Daily Averages. Cite three examples of...Ch. 6.A - 51. Distributions in the News. Find three recent...Ch. 6.A - Prob. 52ECh. 6.B - The lowest score on an exam was 62, the median...Ch. 6.B - Which of the following is not part of a...Ch. 6.B - The lower quartile for wages at a coffee shop is...Ch. 6.B - Is it possible for a distribution to have a mean...Ch. 6.B - Suppose you are given the mean and just one data...Ch. 6.B - The standard deviation is best described as a...Ch. 6.B - What type of data distribution has a negative...Ch. 6.B - In any distribution, it is always true that a. the...Ch. 6.B - Which data set would you expect to have the...Ch. 6.B - Professors Smith, Jones, and Garcia all got the...Ch. 6.B - Consider two grocery stores at which the mean time...Ch. 6.B - Describe how we define and calculate the range of...Ch. 6.B - Prob. 3ECh. 6.B - Prob. 4ECh. 6.B - Prob. 5ECh. 6.B - Prob. 6ECh. 6.B - Both exams had the same range, so they must have...Ch. 6.B - The highest exam score was in the upper quartile...Ch. 6.B - For the 30 students who took the test, the high...Ch. 6.B - I examined the data carefully, and the range was...Ch. 6.B - The standard deviation for the heights of a group...Ch. 6.B - The mean gas mileage of the compact cars we tested...Ch. 6.B - 13. Big Bank Verification. Find the mean and...Ch. 6.B - Prob. 14ECh. 6.B - Comparing Variations. Consider the following data...Ch. 6.B - Prob. 16ECh. 6.B - Comparing Variations. Consider the following data...Ch. 6.B - Comparing Variations. Consider the following data...Ch. 6.B - Understanding Variation. The following exercises...Ch. 6.B - Understanding Variation. The following exercises...Ch. 6.B - Prob. 21ECh. 6.B - Airline Arrival Times. Two airlines have data on...Ch. 6.B - 23. Portfolio Standard Deviation. The book...Ch. 6.B - Defect Rates. Two factories each produce 1000...Ch. 6.B - Batting Standard Deviation. For the past 100...Ch. 6.B - Prob. 26ECh. 6.B - Prob. 27ECh. 6.B - Prob. 28ECh. 6.B - 29. Quality Control. An auto transmission...Ch. 6.B - Web Data Sets. Go to any website that gives data...Ch. 6.B - Prob. 31ECh. 6.B - Prob. 32ECh. 6.B - Prob. 33ECh. 6.B - Prob. 34ECh. 6.C - Graphs of normal distributions a. always look...Ch. 6.C - In a normal distribution, the mean a. is equal to...Ch. 6.C - In a normal distribution, data values farther from...Ch. 6.C - Prob. 4QQCh. 6.C - In a normal distribution, about 2/3 Of the data...Ch. 6.C - Prob. 6QQCh. 6.C - Prob. 7QQCh. 6.C - Prob. 8QQCh. 6.C - An acquaintance tells you that his IQ is in the...Ch. 6.C - Prob. 10QQCh. 6.C - 1. What is a normal distribution? Briefly describe...Ch. 6.C - 2. What is the 68-95-99.7 rule for normal...Ch. 6.C - 3. What is a standard score? How do you find the...Ch. 6.C - Prob. 4ECh. 6.C - Prob. 5ECh. 6.C - The weights of babies born at Belmont Hospital are...Ch. 6.C - The weights of babies born at Belmont Hospital are...Ch. 6.C - On yesterday's mathematics exam, the standard...Ch. 6.C - My professor graded the final on a curve, and she...Ch. 6.C - Jack is the 50th percentile for height, so he is...Ch. 6.C - Prob. 11ECh. 6.C - Prob. 12ECh. 6.C - Prob. 13ECh. 6.C - Prob. 14ECh. 6.C - Prob. 15ECh. 6.C - Prob. 16ECh. 6.C - Prob. 17ECh. 6.C - Prob. 18ECh. 6.C - Prob. 19ECh. 6.C - The 68-95-99.7 Rule. The resting heart rates for a...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Prob. 24ECh. 6.C - Psychology Exam. The scores on a psychology exam...Ch. 6.C - Prob. 26ECh. 6.C - Prob. 27ECh. 6.C - Prob. 28ECh. 6.C - Standard Scores and Percentiles. Use Table 6.3 to...Ch. 6.C - Standard Scores and Percentiles. Use Table 6.3 to...Ch. 6.C - Prob. 31ECh. 6.C - Prob. 32ECh. 6.C - Pregnancy Length. Actual lengths of terms are...Ch. 6.C - Pregnancy Length. Actual lengths of terms are...Ch. 6.C - Prob. 35ECh. 6.C - Prob. 36ECh. 6.C - Prob. 37ECh. 6.C - Prob. 38ECh. 6.C - 39. Is It Likely? Suppose you read that the...Ch. 6.C - Prob. 40ECh. 6.C - GRE Scores. Scores on the verbal Graduate Record...Ch. 6.C - Prob. 42ECh. 6.C - Prob. 43ECh. 6.C - Prob. 44ECh. 6.C - GRE Scores. Scores on the verbal Graduate Record...Ch. 6.C - Prob. 46ECh. 6.C - Prob. 47ECh. 6.C - Prob. 48ECh. 6.C - Prob. 49ECh. 6.C - Normal Demonstration. Do a Web search on the...Ch. 6.C - Normal Distributions. Many data sets described in...Ch. 6.C - Heights of American Men. The heights of American...Ch. 6.D - Prob. 1QQCh. 6.D - Prob. 2QQCh. 6.D - Prob. 3QQCh. 6.D - Prob. 4QQCh. 6.D - Prob. 5QQCh. 6.D - Prob. 6QQCh. 6.D - Consider a survey with a margin of error of 4%. If...Ch. 6.D - Prob. 8QQCh. 6.D - Prob. 9QQCh. 6.D - Prob. 10QQCh. 6.D - Prob. 1ECh. 6.D - Prob. 2ECh. 6.D - Prob. 3ECh. 6.D - Prob. 4ECh. 6.D - Prob. 5ECh. 6.D - Prob. 6ECh. 6.D - Prob. 7ECh. 6.D - Prob. 8ECh. 6.D - Prob. 9ECh. 6.D - Prob. 10ECh. 6.D - Both agencies conducted their surveys carefully,...Ch. 6.D - If you want to reduce the margin of error in your...Ch. 6.D - Prob. 13ECh. 6.D - Prob. 14ECh. 6.D - Prob. 15ECh. 6.D - Prob. 16ECh. 6.D - Prob. 17ECh. 6.D - Prob. 18ECh. 6.D - Prob. 19ECh. 6.D - Prob. 20ECh. 6.D - Human Body Temperature. A study by University of...Ch. 6.D - Seat Belts and Children. In a study of children...Ch. 6.D - SAT Preparation. A study of 75 students who took...Ch. 6.D - Weight by Age. A National Health Survey determined...Ch. 6.D - Margin of Error. Find the margin of error and the...Ch. 6.D - Prob. 26ECh. 6.D - Prob. 27ECh. 6.D - Prob. 28ECh. 6.D - Prob. 29ECh. 6.D - 25-32: Margin of Error. Find the margin of error...Ch. 6.D - Prob. 31ECh. 6.D - Prob. 32ECh. 6.D - Prob. 33ECh. 6.D - Prob. 34ECh. 6.D - Prob. 35ECh. 6.D - Prob. 36ECh. 6.D - Prob. 37ECh. 6.D - Prob. 38ECh. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D -
39-44: Hypothesis Tests. The following exercises...Ch. 6.D - Prob. 44ECh. 6.D - Prob. 45ECh. 6.D - Prob. 46ECh. 6.D - Prob. 47ECh. 6.D - Better Margin of Error. Suppose you want to...Ch. 6.D - Prob. 49ECh. 6.D - Recent Polls. Visit the websites of polling...Ch. 6.D - Prob. 52ECh. 6.D - Statistical Significance. Find a recent news...Ch. 6.D - Prob. 55ECh. 6.D - Hypothesis Testing. Find a news report describing...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 27 Suppose that you have a data set of 1, 2, 2, 3, 3, 3, 4, 4, 5, and you assume that this sample represents a population. The mean is 3 and g the standard deviation is 1.225.10 a. Explain why you can apply the empirical rule to this data set. b. Where would "most of the values" in the population fall, based on this data set?arrow_forward30 Explain how you can use the empirical rule to find out whether a data set is mound- shaped, using only the values of the data themselves (no histogram available).arrow_forward5. Let X be a positive random variable with finite variance, and let A = (0, 1). Prove that P(X AEX) 2 (1-A)² (EX)² EX2arrow_forward
- 6. Let, for p = (0, 1), and xe R. X be a random variable defined as follows: P(X=-x) = P(X = x)=p. P(X=0)= 1-2p. Show that there is equality in Chebyshev's inequality for X. This means that Chebyshev's inequality, in spite of being rather crude, cannot be improved without additional assumptions.arrow_forward4. Prove that, for any random variable X, the minimum of EIX-al is attained for a = med (X).arrow_forward8. Recall, from Sect. 2.16.4, the likelihood ratio statistic, Ln, which was defined as a product of independent, identically distributed random variables with mean 1 (under the so-called null hypothesis), and the, sometimes more convenient, log-likelihood, log L, which was a sum of independent, identically distributed random variables, which, however, do not have mean log 1 = 0. (a) Verify that the last claim is correct, by proving the more general statement, namely that, if Y is a non-negative random variable with finite mean, then E(log Y) log(EY). (b) Prove that, in fact, there is strict inequality: E(log Y) < log(EY), unless Y is degenerate. (c) Review the proof of Jensen's inequality, Theorem 5.1. Generalize with a glimpse on (b).arrow_forward
- 2. Derive the component transformation equations for tensors shown be- low where [C] = [BA] is the direction cosine matrix from frame A to B. B[T] = [C]^[T][C]T 3. The transport theorem for vectors shows that the time derivative can be constructed from two parts: the first is an explicit frame-dependent change of the vector whereas the second is an active rotational change of the vector. The same holds true for tensors. Starting from the previous result, derive a version of transport theorem for tensors. [C] (^[T])[C] = dt d B dt B [T] + [WB/A]B[T] – TWB/A] (10 pt) (7pt)arrow_forwardUse the graph of the function y = f (x) to find the value, if possible. f(x) 8 7 6 Q5 y 3 2 1 x -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 -4 -5 -6 -7 -8+ Olim f(z) x-1+ O Limit does not exist.arrow_forward3. Prove that, for any random variable X, the minimum of E(X - a)² is attained for a = EX. Provedarrow_forward
- Shade the areas givenarrow_forward7. Cantelli's inequality. Let X be a random variable with finite variance, o². (a) Prove that, for x ≥ 0, P(X EX2x)≤ 02 x² +0² 202 P(|X - EX2x)<≤ (b) Find X assuming two values where there is equality. (c) When is Cantelli's inequality better than Chebyshev's inequality? (d) Use Cantelli's inequality to show that med (X) - EX ≤ o√√3; recall, from Proposition 6.1, that an application of Chebyshev's inequality yields the bound o√√2. (e) Generalize Cantelli's inequality to moments of order r 1.arrow_forwardThe college hiking club is having a fundraiser to buy new equipment for fall and winter outings. The club is selling Chinese fortune cookies at a price of $2 per cookie. Each cookie contains a piece of paper with a different number written on it. A random drawing will determine which number is the winner of a dinner for two at a local Chinese restaurant. The dinner is valued at $32. Since fortune cookies are donated to the club, we can ignore the cost of the cookies. The club sold 718 cookies before the drawing. Lisa bought 13 cookies. Lisa's expected earnings can be found by multiplying the value of the dinner by the probability that she will win. What are Lisa's expected earnings? Round your answer to the nearest cent.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
How to make Frequency Distribution Table / Tally Marks and Frequency Distribution Table; Author: Reenu Math;https://www.youtube.com/watch?v=i_A6RiE8tLE;License: Standard YouTube License, CC-BY
Frequency distribution table in statistics; Author: Math and Science;https://www.youtube.com/watch?v=T7KYO76DoOE;License: Standard YouTube License, CC-BY
Frequency Distribution Table for Grouped/Continuous data | Math Dot Com; Author: Maths dotcom;https://www.youtube.com/watch?v=ErnccbXQOPY;License: Standard Youtube License