
i.
To make a tree diagram to show all the different possible outcomes.
i.
Answer to Problem 16E
The tree diagram with the possible outcomes can be drawn as:
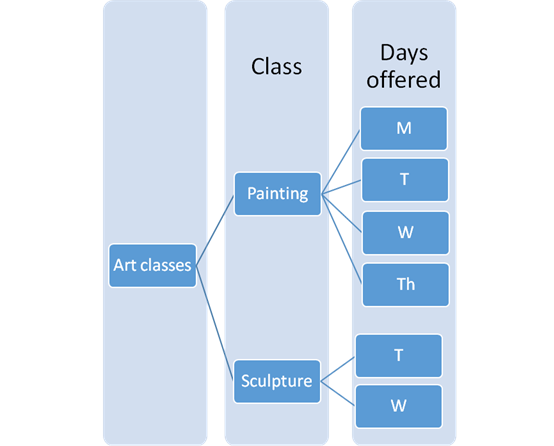
Explanation of Solution
Given:
The table provided in the question is:
| Class | Days offered |
| Painting | M, T, W, Th |
| Sculpture | T, W |
Painting class is on Monday, Tuesday, Wednesday and Thursday.
Sculpture class is on Tuesday and Wednesday.
There can be only one Painting and one Sculpture class per week.
Calculation:
The tree diagram with the possible outcomes can be drawn as:
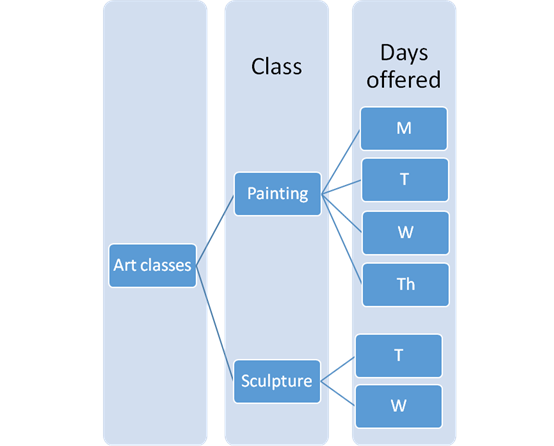
ii.
To find different possible schedules for the two classes.
ii.
Answer to Problem 16E
There are total of
Explanation of Solution
Given:
The table provided in the question is:
| Class | Days offered |
| Painting | M, T, W, Th |
| Sculpture | T, W |
Painting class is on Monday, Tuesday, Wednesday and Thursday.
Sculpture class is on Tuesday and Wednesday.
There can be only one Painting and one Sculpture class per week.
Calculation:
The tree diagram with the possible outcomes can be drawn as:
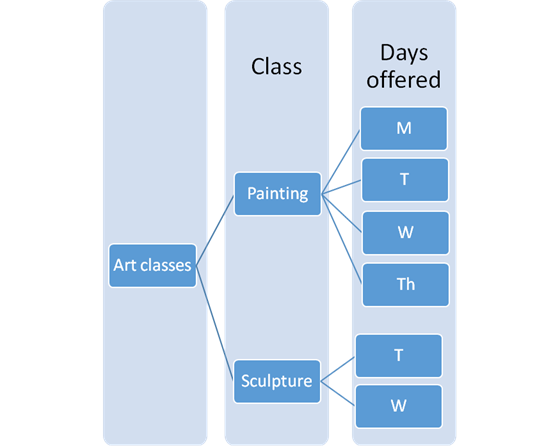
As conclude from the tree diagram there are total of
Hence,
There are total of
iii.
To find the probability.
iii.
Answer to Problem 16E
There are
Explanation of Solution
Given:
The table provided in the question is:
| Class | Days offered |
| Painting | M, T, W, Th |
| Sculpture | T, W |
Painting class is on Monday, Tuesday, Wednesday and Thursday.
Sculpture class is on Tuesday and Wednesday.
There can be only one Painting and one Sculpture class per week.
Formula used:
Calculation:
The tree diagram with the possible outcomes is shown as:
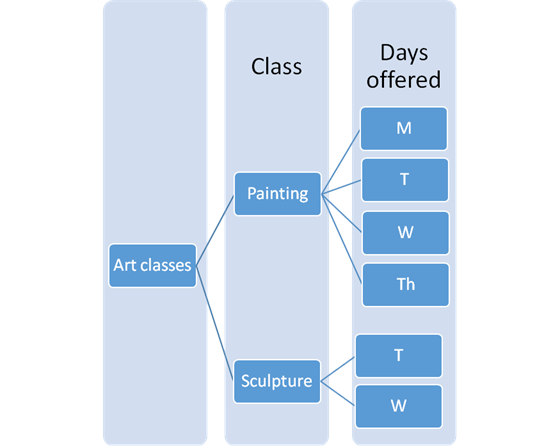
As from the tree diagram total number of outcomes is
Chances of Sculpture class schedule on Tuesday from all the outcomes is
Therefore,
Hence,
Probability of sculpture class in on Tuesday is
iv.
To explain the statement.
iv.
Answer to Problem 16E
It is better to make a tree diagram than to use the multiplication principle because a tree diagram is a simple way of representing a sequence of events and are useful in probability since they record all possible outcomes in a clear and uncomplicated manner and in a situation like this it is better to used tree diagram since it clearly shows the outcomes and eliminates the possibilities of the event occurring on the same day.
Explanation of Solution
Given:
The table provided in the question is:
| Class | Days offered |
| Painting | M, T, W, Th |
| Sculpture | T, W |
Painting class is on Monday, Tuesday, Wednesday and Thursday.
Sculpture class is on Tuesday and Wednesday.
There can be only one Painting and one Sculpture class per week.
Calculation:
It is better to make a tree diagram than to use the multiplication principle because a tree diagram is a simple way of representing a sequence of events and are useful in probability since they record all possible outcomes in a clear and uncomplicated manner and in a situation like this it is better to used tree diagram since it clearly shows the outcomes and eliminates the possibilities of the event occurring on the same day.
Chapter 6 Solutions
EBK PRE-ALGEBRA
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Precalculus
Thinking Mathematically (6th Edition)
Algebra and Trigonometry (6th Edition)
Elementary Statistics
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- Graph without using the calculator y-1 = | x+4 |arrow_forward9:43 AS く Akbar © Printed in the United States 15) Scale: 1 cmal unit on both axes .ill 64% The graph above shows a straight line QT intersecting the y-axis at T. i State the co-ordinates of T. ii Calculate the gradient of QT 16) iii Determine the equation of QT. A (-1, 9) ||| i L Г (5 marks)arrow_forwardPls help.arrow_forward
- Solve the system of equation for y using Cramer's rule. Hint: The determinant of the coefficient matrix is -23. - 5x + y − z = −7 2x-y-2z = 6 3x+2z-7arrow_forwarderic pez Xte in z= Therefore, we have (x, y, z)=(3.0000, 83.6.1 Exercise Gauss-Seidel iteration with Start with (x, y, z) = (0, 0, 0). Use the convergent Jacobi i Tol=10 to solve the following systems: 1. 5x-y+z = 10 2x-8y-z=11 -x+y+4z=3 iteration (x Assi 2 Assi 3. 4. x-5y-z=-8 4x-y- z=13 2x - y-6z=-2 4x y + z = 7 4x-8y + z = -21 -2x+ y +5z = 15 4x + y - z=13 2x - y-6z=-2 x-5y- z=-8 realme Shot on realme C30 2025.01.31 22:35 farrow_forwardUse Pascal's triangle to expand the binomial (6m+2)^2arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





