CODE/CALC ET 3-HOLE
CODE/CALC ET 3-HOLE
2nd Edition
ISBN: 9781323178522
Author: Briggs
Publisher: PEARSON
bartleby

Concept explainers

Cylinders
A cylinder is a three-dimensional solid shape with two parallel and congruent circular bases, joined by a curved surface at a fixed distance. A cylinder has an infinite curvilinear surface.
Cones
A cone is a three-dimensional solid shape having a flat base and a pointed edge at the top. The flat base of the cone tapers smoothly to form the pointed edge known as the apex. The flat base of the cone can either be circular or elliptical. A cone is dr…
bartleby

Videos

Textbook Question
Book Icon
Chapter 6.7, Problem 28E

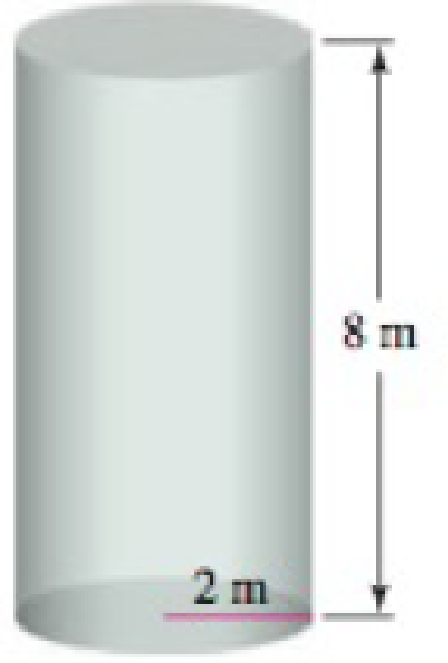
Emptying a cylindrical tank A cylindrical water tank has height 8 m and radius 2 m (see figure).

  1. a. If the tank is full of water, how much work is required to pump the water to the level of the top of the tank and out of the tank?
  2. b. Is it true that it takes half as much work to pump the water out of the tank when it is half full as when it is full? Explain.

Chapter 6.7, Problem 28E, Emptying a cylindrical tank A cylindrical water tank has height 8 m and radius 2 m (see figure). a.

Expert Solution & Answer
Check Mark
bartleby

Learn your wayIncludes step-by-step video

See solution
Check out sample textbook solution
Blurred answer
10:29
Previous
Chapter 6.7, Problem 27E
Next
Chapter 6.7, Problem 29E

Chapter 6 Solutions

CODE/CALC ET 3-HOLE

Ch. 6.1 - Explain the meaning of position, displacement, and...Ch. 6.1 - Suppose the velocity of an object moving along a...Ch. 6.1 - Given the velocity function v of an object moving...Ch. 6.1 - Explain how to use definite integrals to find the...Ch. 6.1 - Prob. 5ECh. 6.1 - What is the result of integrating a population...Ch. 6.1 - Displacement and distance from velocity Consider...Ch. 6.1 - Prob. 8ECh. 6.1 - Displacement from velocity Assume t is time...Ch. 6.1 - Displacement from velocity Assume t is time...
Ch. 6.1 - Displacement from velocity Assume t is time...Ch. 6.1 - Displacement from velocity Assume t is time...Ch. 6.1 - Prob. 13ECh. 6.1 - Displacement from velocity Assume t is time...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Prob. 16ECh. 6.1 - Prob. 17ECh. 6.1 - Prob. 18ECh. 6.1 - Prob. 19ECh. 6.1 - Prob. 20ECh. 6.1 - Oscillating motion A mass hanging from a spring is...Ch. 6.1 - Cycling distance A cyclist rides down a long...Ch. 6.1 - Flying into a headwind The velocity (in mi/hr) of...Ch. 6.1 - Day hike The velocity (in mi/hr) of a hiker...Ch. 6.1 - Piecewise velocity The velocity of a (fast)...Ch. 6.1 - Probe speed A data collection probe is dropped...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Prob. 28ECh. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Prob. 30ECh. 6.1 - Prob. 31ECh. 6.1 - Prob. 32ECh. 6.1 - Prob. 33ECh. 6.1 - Prob. 34ECh. 6.1 - Prob. 35ECh. 6.1 - Prob. 36ECh. 6.1 - Approaching a station At t = 0, a train...Ch. 6.1 - Prob. 38ECh. 6.1 - Oil production An oil refinery produces oil at a...Ch. 6.1 - Population growth 40. Starting with an initial...Ch. 6.1 - Population growth 41. When records were first kept...Ch. 6.1 - Population growth 42. The population of a...Ch. 6.1 - Population growth 43. A culture of bacteria in a...Ch. 6.1 - Flow rates in the Spokane River The daily...Ch. 6.1 - Marginal cost Consider the following marginal cost...Ch. 6.1 - Marginal cost Consider the following marginal cost...Ch. 6.1 - Marginal cost Consider the following marginal cost...Ch. 6.1 - Prob. 48ECh. 6.1 - Explain why or why not Determine whether the...Ch. 6.1 - Velocity graphs The figures show velocity...Ch. 6.1 - Velocity graphs The figures show velocity...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Where do they meet? Kelly started at noon (t = 0)...Ch. 6.1 - Prob. 57ECh. 6.1 - Two runners At noon (t = 0), Alicia starts running...Ch. 6.1 - Prob. 59ECh. 6.1 - Filling a tank A 2000-liter cistern is empty when...Ch. 6.1 - Depletion of natural resources Suppose that r(t) =...Ch. 6.1 - Snowplow problem With snow on the ground and...Ch. 6.1 - Filling a reservoir A reservoir with a capacity of...Ch. 6.1 - Blood flow A typical human heart pumps 70 mL of...Ch. 6.1 - Prob. 65ECh. 6.1 - Oscillating growth rates Some species have growth...Ch. 6.1 - Power and energy Power and energy are often used...Ch. 6.1 - Variable gravity At Earths surface, the...Ch. 6.1 - Another look at the Fundamental Theorem 69....Ch. 6.1 - Another look at the Fundamental Theorem 70. Use...Ch. 6.1 - Another look at the Fundamental Theorem 71. Use...Ch. 6.1 - Another look at the Fundamental Theorem 72....Ch. 6.2 - Draw the graphs of two functions f and g that are...Ch. 6.2 - Prob. 2ECh. 6.2 - Make a sketch to show a case in which the area...Ch. 6.2 - Make a sketch to show a case in which the area...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Regions between curves Sketch the region and find...Ch. 6.2 - Prob. 10ECh. 6.2 - Regions between curves Sketch the region and find...Ch. 6.2 - Regions between curves Sketch the region and find...Ch. 6.2 - Prob. 13ECh. 6.2 - Regions between curves Sketch the region and find...Ch. 6.2 - Prob. 15ECh. 6.2 - Prob. 16ECh. 6.2 - Prob. 17ECh. 6.2 - Prob. 18ECh. 6.2 - Compound regions Sketch each region (if a figure...Ch. 6.2 - Compound regions Sketch each region (if a figure...Ch. 6.2 - Compound regions Sketch each region (if a figure...Ch. 6.2 - Compound regions Sketch each region (if a figure...Ch. 6.2 - Integrating with respect to y Determine the area...Ch. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - Prob. 27ECh. 6.2 - Two approaches Express the area of the following...Ch. 6.2 - Prob. 29ECh. 6.2 - Two approaches Express the area of the following...Ch. 6.2 - Two approaches Find the area of the following...Ch. 6.2 - Prob. 32ECh. 6.2 - Any method Use any method (including geometry) to...Ch. 6.2 - Prob. 34ECh. 6.2 - Prob. 35ECh. 6.2 - Any method Use any method (including geometry) to...Ch. 6.2 - Any method Use any method (including geometry) to...Ch. 6.2 - Any method Use any method (including geometry) to...Ch. 6.2 - Explain why or why not Determine whether the...Ch. 6.2 - Regions between curves Sketch the region and find...Ch. 6.2 - Prob. 41ECh. 6.2 - Prob. 42ECh. 6.2 - Prob. 43ECh. 6.2 - Prob. 44ECh. 6.2 - Prob. 45ECh. 6.2 - Prob. 46ECh. 6.2 - Prob. 47ECh. 6.2 - Either method Use the most efficient strategy for...Ch. 6.2 - Prob. 49ECh. 6.2 - Prob. 50ECh. 6.2 - Comparing areas Let f(x) = xp and g(x) = x1/q,...Ch. 6.2 - Complicated regions Find the area of the regions...Ch. 6.2 - Complicated regions Find the area of the regions...Ch. 6.2 - Complicated regions Find the area of the regions...Ch. 6.2 - Prob. 55ECh. 6.2 - Prob. 56ECh. 6.2 - Prob. 57ECh. 6.2 - Prob. 58ECh. 6.2 - Prob. 59ECh. 6.2 - Prob. 60ECh. 6.2 - Bisecting regions For each region R, find the...Ch. 6.2 - Prob. 62ECh. 6.2 - Prob. 63ECh. 6.2 - Geometric probability Suppose a dartboard occupies...Ch. 6.2 - Lorenz curves and the Gini index A Lorenz curve is...Ch. 6.2 - Equal area properties for parabolas Consider the...Ch. 6.2 - Minimum area Graph the curves y = (x + 1)(x 2)...Ch. 6.2 - Prob. 68ECh. 6.2 - Area of a curve defined implicitly Determine the...Ch. 6.2 - Prob. 70ECh. 6.2 - Area function for a cubic Consider the cubic...Ch. 6.2 - Differences of even functions Assume f and g are...Ch. 6.2 - Prob. 73ECh. 6.2 - Shifting sines Consider the functions f(x) = a sin...Ch. 6.3 - Suppose a cut is made through a solid object...Ch. 6.3 - A solid has a circular base and cross sections...Ch. 6.3 - Prob. 3ECh. 6.3 - Prob. 4ECh. 6.3 - Why is the disk method a special case of the...Ch. 6.3 - Prob. 6ECh. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - Prob. 10ECh. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - Prob. 12ECh. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - Prob. 14ECh. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Prob. 23ECh. 6.3 - Prob. 24ECh. 6.3 - Prob. 25ECh. 6.3 - Prob. 26ECh. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Prob. 31ECh. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Prob. 37ECh. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Which is greater? For the following regions R,...Ch. 6.3 - Prob. 42ECh. 6.3 - Prob. 43ECh. 6.3 - Prob. 44ECh. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Prob. 52ECh. 6.3 - Explain why or why not Determine whether the...Ch. 6.3 - Prob. 54ECh. 6.3 - Prob. 55ECh. 6.3 - Prob. 56ECh. 6.3 - Prob. 57ECh. 6.3 - Prob. 58ECh. 6.3 - Prob. 59ECh. 6.3 - Prob. 60ECh. 6.3 - Fermats volume calculation (1636) Let R be the...Ch. 6.3 - Solid from a piecewise function Let...Ch. 6.3 - Prob. 63ECh. 6.3 - Volume of a wooden object A solid wooden object...Ch. 6.3 - Cylinder, cone, hemisphere A right circular...Ch. 6.3 - Water in a bowl A hemispherical bowl of radius 8...Ch. 6.3 - A torus (doughnut) Find the volume of the torus...Ch. 6.3 - Which is greater? Let R be the region bounded by y...Ch. 6.3 - Prob. 69ECh. 6.3 - Prob. 70ECh. 6.4 - Assume f and g are continuous with f(x) g(x) on...Ch. 6.4 - Fill in the blanks: A region R is revolved about...Ch. 6.4 - Fill in the blanks: A region R is revolved about...Ch. 6.4 - Prob. 4ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 8ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 11ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Prob. 16ECh. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Prob. 31ECh. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Washers vs. shells Let R be the region bounded by...Ch. 6.4 - Prob. 42ECh. 6.4 - Prob. 43ECh. 6.4 - Washers vs. shells Let R be the region bounded by...Ch. 6.4 - Prob. 45ECh. 6.4 - Prob. 46ECh. 6.4 - Washers vs. shells Let R be the region bounded by...Ch. 6.4 - Prob. 48ECh. 6.4 - Explain why or why not Determine whether the...Ch. 6.4 - Prob. 50ECh. 6.4 - Prob. 51ECh. 6.4 - Prob. 52ECh. 6.4 - Prob. 53ECh. 6.4 - Prob. 54ECh. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Prob. 58ECh. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - The solid formed when the region bounded by y=x,...Ch. 6.4 - Prob. 63ECh. 6.4 - A hemisphere by three methods Let R be the region...Ch. 6.4 - Prob. 65ECh. 6.4 - A spherical cap by three methods Consider the cap...Ch. 6.4 - Prob. 67ECh. 6.4 - Wedge from a tree Imagine a cylindrical tree of...Ch. 6.4 - Prob. 69ECh. 6.4 - Prob. 70ECh. 6.4 - Prob. 71ECh. 6.4 - Ellipsoids An ellipse centered at the origin is...Ch. 6.4 - Change of variables Suppose f(x) 0 for all x and...Ch. 6.4 - Equal integrals Without evaluating integrals,...Ch. 6.4 - Volumes without calculus Solve the following...Ch. 6.5 - Explain the steps required to find the length of a...Ch. 6.5 - Explain the steps required to find the length of a...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc lezngth calculations Find the arc length of...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Prob. 15ECh. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Prob. 29ECh. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Explain why or why not Determine whether the...Ch. 6.5 - Arc length for a line Consider the segment of the...Ch. 6.5 - Functions from arc length What differentiable...Ch. 6.5 - Function from arc length Find a curve that passes...Ch. 6.5 - Prob. 35ECh. 6.5 - Prob. 36ECh. 6.5 - Golden Gate cables The profile of the cables on a...Ch. 6.5 - Gateway Arch The shape of the Gateway Arch in St....Ch. 6.5 - Lengths of related curves Suppose the graph of f...Ch. 6.5 - Prob. 40ECh. 6.5 - A family of exponential functions a. Show that the...Ch. 6.5 - Bernoullis parabolas Johann Bernoulli (16671748)...Ch. 6.6 - What is the area of the curved surface of a right...Ch. 6.6 - A frustum of a cone is generated by revolving the...Ch. 6.6 - Suppose f is positive and differentiable on [a,...Ch. 6.6 - Suppose g is positive and differentiable on [c,...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Prob. 9ECh. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Prob. 12ECh. 6.6 - Prob. 13ECh. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Painting surfaces A 1.5-mm layer of paint is...Ch. 6.6 - Painting surfaces A 1.5-mm layer of paint is...Ch. 6.6 - Revolving about the y-axis Find the area of the...Ch. 6.6 - Revolving about the y-axis Find the area of the...Ch. 6.6 - Revolving about the y-axis Find the area of the...Ch. 6.6 - Revolving about the y-axis Find the area of the...Ch. 6.6 - Explain why or why not Determine whether the...Ch. 6.6 - Surface area calculations Use the method of your...Ch. 6.6 - Surface area calculations Use the method of your...Ch. 6.6 - Surface area calculations Use the method of your...Ch. 6.6 - Prob. 25ECh. 6.6 - Prob. 26ECh. 6.6 - T 2629. Surface area using technology Consider the...Ch. 6.6 - Prob. 28ECh. 6.6 - Surface area using technology Consider the...Ch. 6.6 - Cones and cylinders The volume of a cone of radius...Ch. 6.6 - Prob. 31ECh. 6.6 - Surface area of a torus When the circle x2 + (y ...Ch. 6.6 - Zones of a sphere Suppose a sphere of radius r is...Ch. 6.6 - Prob. 34ECh. 6.6 - Surface-area-to-volume ratio (SAV) In the design...Ch. 6.6 - Surface area of a frustum Show that the surface...Ch. 6.6 - Scaling surface area Let f be a nonnegative...Ch. 6.6 - Surface plus cylinder Suppose f is a nonnegative...Ch. 6.7 - Suppose a 1-m cylindrical bar has a constant...Ch. 6.7 - Explain how to find the mass of a one-dimensional...Ch. 6.7 - How much work is required to move an object from x...Ch. 6.7 - Why is integration used to find the work done by a...Ch. 6.7 - Why is integration used to find the work required...Ch. 6.7 - Why is integration used to find the total force on...Ch. 6.7 - What is the pressure on a horizontal surface with...Ch. 6.7 - Explain why you integrate in the vertical...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Work from force How much work is required to move...Ch. 6.7 - Work from force How much work is required to move...Ch. 6.7 - Compressing and stretching a spring Suppose a...Ch. 6.7 - Compressing and stretching a spring Suppose a...Ch. 6.7 - Work done by a spring A spring on a horizontal...Ch. 6.7 - Shock absorber A heavy-duty shock absorber is...Ch. 6.7 - Calculating work for different springs Calculate...Ch. 6.7 - Calculating work for different springs Calculate...Ch. 6.7 - Calculating work for different springs Calculate...Ch. 6.7 - Work function A spring has a restoring force given...Ch. 6.7 - Emptying a swimming pool A swimming pool has the...Ch. 6.7 - Emptying a cylindrical tank A cylindrical water...Ch. 6.7 - Emptying a half-full cylindrical tank Suppose the...Ch. 6.7 - Emptying a partially filled swimming pool If the...Ch. 6.7 - Emptying a conical tank A water tank is shaped...Ch. 6.7 - Emptying a real swimming pool A swimming pool is...Ch. 6.7 - Prob. 33ECh. 6.7 - Emptying a water trough A water trough has a...Ch. 6.7 - Emptying a water trough A cattle trough has a...Ch. 6.7 - Prob. 36ECh. 6.7 - Emptying a conical tank An inverted cone is 2 m...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Parabolic dam The lower edge of a dam is defined...Ch. 6.7 - Prob. 43ECh. 6.7 - Force on the end of a tank Determine the force on...Ch. 6.7 - Force on a building A large building shaped like a...Ch. 6.7 - Force on a window A diving pool that is 4 m deep...Ch. 6.7 - Force on a window A diving pool that is 4 m deep...Ch. 6.7 - Force on a window A diving pool that is 4 m deep...Ch. 6.7 - Explain why or why not Determine whether the...Ch. 6.7 - Prob. 50ECh. 6.7 - A nonlinear spring Hookes law is applicable to...Ch. 6.7 - Prob. 52ECh. 6.7 - Drinking juice A glass has circular cross sections...Ch. 6.7 - Upper and lower half A cylinder with height 8 m...Ch. 6.7 - Work in a gravitational field For large distances...Ch. 6.7 - Prob. 56ECh. 6.7 - Winding a chain A 30-m-long chain hangs vertically...Ch. 6.7 - Coiling a rope A 60-m-long, 9.4-mm-diameter rope...Ch. 6.7 - Lifting a pendulum A body of mass m is suspended...Ch. 6.7 - Prob. 60ECh. 6.7 - Prob. 61ECh. 6.7 - Prob. 62ECh. 6.7 - Critical depth A large tank has a plastic window...Ch. 6.7 - Buoyancy Archimedes principle says that the...Ch. 6.8 - Prob. 1ECh. 6.8 - Prob. 2ECh. 6.8 - Evaluate 4xdx.Ch. 6.8 - What is the inverse function of ln x, and what are...Ch. 6.8 - Express 3x, x, and xsin x using the base e.Ch. 6.8 - Evaluate ddx(3x).Ch. 6.8 - Prob. 7ECh. 6.8 - Derivatives with ln x Evaluate the following...Ch. 6.8 - Derivatives with ln x Evaluate the following...Ch. 6.8 - Derivatives with ln x Evaluate the following...Ch. 6.8 - Derivatives with ln x Evaluate the following...Ch. 6.8 - Derivatives with ln x Evaluate the following...Ch. 6.8 - Integrals with ln x Evaluate the following...Ch. 6.8 - Prob. 14ECh. 6.8 - Integrals with ln x Evaluate the following...Ch. 6.8 - Integrals with ln x Evaluate the following...Ch. 6.8 - Integrals with ln x Evaluate the following...Ch. 6.8 - Integrals with ln x Evaluate the following...Ch. 6.8 - Integrals with ln x Evaluate the following...Ch. 6.8 - Integrals with ln x Evaluate the following...Ch. 6.8 - Integrals with ex Evaluate the following...Ch. 6.8 - Integrals with ex Evaluate the following...Ch. 6.8 - Integrals with ex Evaluate the following...Ch. 6.8 - Integrals with ex Evaluate the following...Ch. 6.8 - Integrals with ex Evaluate the following...Ch. 6.8 - Integrals with ex Evaluate the following...Ch. 6.8 - Integrals with general bases Evaluate the...Ch. 6.8 - Integrals with general bases Evaluate the...Ch. 6.8 - Integrals with general bases Evaluate the...Ch. 6.8 - Integrals with general bases Evaluate the...Ch. 6.8 - Integrals with general bases Evaluate the...Ch. 6.8 - Integrals with general bases Evaluate the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Derivatives Evaluate the derivatives of the...Ch. 6.8 - Prob. 41ECh. 6.8 - Prob. 42ECh. 6.8 - Prob. 43ECh. 6.8 - Prob. 44ECh. 6.8 - Prob. 45ECh. 6.8 - Prob. 46ECh. 6.8 - Prob. 47ECh. 6.8 - Prob. 48ECh. 6.8 - Prob. 49ECh. 6.8 - Miscellaneous derivatives Compute the following...Ch. 6.8 - Miscellaneous derivatives Compute the following...Ch. 6.8 - Prob. 52ECh. 6.8 - Miscellaneous derivatives Compute the following...Ch. 6.8 - Miscellaneous derivatives Compute the following...Ch. 6.8 - Miscellaneous derivatives Compute the following...Ch. 6.8 - Miscellaneous derivatives Compute the following...Ch. 6.8 - Miscellaneous derivatives Compute the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Miscellaneous integrals Evaluate the following...Ch. 6.8 - Probability as an integral Two points P and Q are...Ch. 6.8 - Prob. 70ECh. 6.8 - Prob. 71ECh. 6.8 - Prob. 72ECh. 6.8 - Prob. 73ECh. 6.8 - Prob. 74ECh. 6.8 - Prob. 75ECh. 6.9 - In terms of relative growth rate, what is the...Ch. 6.9 - Prob. 2ECh. 6.9 - Prob. 3ECh. 6.9 - Prob. 4ECh. 6.9 - Prob. 5ECh. 6.9 - Prob. 6ECh. 6.9 - Give two examples of processes that are modeled by...Ch. 6.9 - Give two examples of processes that are modeled by...Ch. 6.9 - Absolute and relative growth rates Two functions f...Ch. 6.9 - Absolute and relative growth rates Two functions f...Ch. 6.9 - Designing exponential growth functions Devise the...Ch. 6.9 - Prob. 12ECh. 6.9 - Prob. 13ECh. 6.9 - Prob. 14ECh. 6.9 - Prob. 15ECh. 6.9 - Designing exponential growth functions Devise the...Ch. 6.9 - Projection sensitivity According to the 2010...Ch. 6.9 - Energy consumption On the first day of the year (t...Ch. 6.9 - Prob. 19ECh. 6.9 - Prob. 20ECh. 6.9 - Prob. 21ECh. 6.9 - Designing exponential decay functions Devise an...Ch. 6.9 - Designing exponential decay functions Devise an...Ch. 6.9 - Designing exponential decay functions Devise an...Ch. 6.9 - Prob. 25ECh. 6.9 - Prob. 26ECh. 6.9 - Atmospheric pressure The pressure of Earths...Ch. 6.9 - Carbon dating The half-life of C-14 is about 5730...Ch. 6.9 - Uranium dating Uranium-238 (U-238) has a half-life...Ch. 6.9 - Radioiodine treatment Roughly 12,000 Americans are...Ch. 6.9 - Explain why or why not Determine whether the...Ch. 6.9 - Tripling time A quantity increases according to...Ch. 6.9 - Constant doubling time Prove that the doubling...Ch. 6.9 - Prob. 34ECh. 6.9 - A slowing race Starting at the same time and...Ch. 6.9 - Prob. 36ECh. 6.9 - Compounded inflation The U.S. government reports...Ch. 6.9 - Acceleration, velocity, position Suppose the...Ch. 6.9 - Air resistance (adapted from Putnam Exam, 1939) An...Ch. 6.9 - A running model A model for the startup of a...Ch. 6.9 - Tumor growth Suppose the cells of a tumor are...Ch. 6.9 - Prob. 42ECh. 6.9 - Prob. 43ECh. 6.9 - Geometric means A quantity grows exponentially...Ch. 6.9 - Equivalent growth functions The same exponential...Ch. 6.9 - General relative growth rates Define the relative...Ch. 6.10 - State the definition of the hyperbolic cosine and...Ch. 6.10 - Sketch the graphs of y = cosh x, y sinh x, and y...Ch. 6.10 - What is the fundamental identity for hyperbolic...Ch. 6.10 - Prob. 4ECh. 6.10 - Express sinh1 x in terms of logarithms.Ch. 6.10 - Prob. 6ECh. 6.10 - Prob. 7ECh. 6.10 - On what interval is the formula d/dx (tanh1 x) =...Ch. 6.10 - Prob. 9ECh. 6.10 - Prob. 10ECh. 6.10 - Verifying identities Verify each identity using...Ch. 6.10 - Verifying identities Verify each identity using...Ch. 6.10 - Verifying identities Verify each identity using...Ch. 6.10 - Verifying identities Verify each identity using...Ch. 6.10 - Verifying identities Verify each identity using...Ch. 6.10 - Verifying identities Use the given identity to...Ch. 6.10 - Verifying identities Use the given identity to...Ch. 6.10 - Prob. 18ECh. 6.10 - Derivative formulas Derive the following...Ch. 6.10 - Derivative formulas Derive the following...Ch. 6.10 - Derivative formulas Derive the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Derivatives Compute dy/dx for the following...Ch. 6.10 - Prob. 30ECh. 6.10 - Indefinite integrals Determine each indefinite...Ch. 6.10 - Prob. 32ECh. 6.10 - Indefinite integrals Determine each indefinite...Ch. 6.10 - Indefinite integrals Determine each indefinite...Ch. 6.10 - Indefinite integrals Determine each indefinite...Ch. 6.10 - Indefinite integrals Determine each indefinite...Ch. 6.10 - Definite integrals Evaluate each definite...Ch. 6.10 - Prob. 38ECh. 6.10 - Definite integrals Evaluate each definite...Ch. 6.10 - Definite integrals Evaluate each definite...Ch. 6.10 - Two ways Evaluate the following integrals two...Ch. 6.10 - Two ways Evaluate the following integrals two...Ch. 6.10 - Visual approximation a. Use a graphing utility to...Ch. 6.10 - Prob. 44ECh. 6.10 - Prob. 45ECh. 6.10 - Points of intersection and area a. Sketch the...Ch. 6.10 - Derivatives Find the derivatives of the following...Ch. 6.10 - Derivatives Find the derivatives of the following...Ch. 6.10 - Derivatives Find the derivatives of the following...Ch. 6.10 - Derivatives Find the derivatives of the following...Ch. 6.10 - Prob. 51ECh. 6.10 - Prob. 52ECh. 6.10 - Indefinite integrals Determine the following...Ch. 6.10 - Prob. 54ECh. 6.10 - Indefinite integrals Determine the following...Ch. 6.10 - Prob. 56ECh. 6.10 - Indefinite integrals Determine the following...Ch. 6.10 - Prob. 58ECh. 6.10 - Prob. 59ECh. 6.10 - Prob. 60ECh. 6.10 - Prob. 61ECh. 6.10 - Prob. 62ECh. 6.10 - Prob. 63ECh. 6.10 - Prob. 64ECh. 6.10 - Catenary arch The portion of the curve y=1716coshx...Ch. 6.10 - Length of a catenary Show that the arc length of...Ch. 6.10 - Power lines A power line is attached at the same...Ch. 6.10 - Sag angle Imagine a climber clipping onto the rope...Ch. 6.10 - Wavelength The velocity of a surface wave on the...Ch. 6.10 - Wave velocity Use Exercise 69 to do the following...Ch. 6.10 - Prob. 71ECh. 6.10 - Tsunamis A tsunami is an ocean wave often caused...Ch. 6.10 - Explain why or why not Determine whether the...Ch. 6.10 - Evaluating hyperbolic functions Use a calculator...Ch. 6.10 - Evaluating hyperbolic functions Evaluate each...Ch. 6.10 - Confirming a graph The graph of f(x) = sinh x is...Ch. 6.10 - Critical points Find the critical points of the...Ch. 6.10 - Critical points a. Show that the critical points...Ch. 6.10 - Points of inflection Find the x-coordinate of the...Ch. 6.10 - Prob. 80ECh. 6.10 - Area of region Find the area of the region bounded...Ch. 6.10 - Prob. 82ECh. 6.10 - LHpital loophole Explain why lHpitals Rule fails...Ch. 6.10 - Limits Use lHpitals Rule to evaluate the following...Ch. 6.10 - Limits Use lHpitals Rule to evaluate the following...Ch. 6.10 - Prob. 86ECh. 6.10 - Prob. 87ECh. 6.10 - Prob. 88ECh. 6.10 - Additional integrals Evaluate the following...Ch. 6.10 - Additional integrals Evaluate the following...Ch. 6.10 - Prob. 91ECh. 6.10 - Additional integrals Evaluate the following...Ch. 6.10 - Kiln design Find the volume interior to the...Ch. 6.10 - Prob. 94ECh. 6.10 - Falling body When an object falling from rest...Ch. 6.10 - Prob. 96ECh. 6.10 - Prob. 97ECh. 6.10 - Prob. 98ECh. 6.10 - Prob. 99ECh. 6.10 - Prob. 100ECh. 6.10 - Prob. 101ECh. 6.10 - Prob. 102ECh. 6.10 - Prob. 103ECh. 6.10 - Prob. 104ECh. 6.10 - Prob. 105ECh. 6.10 - Prob. 106ECh. 6.10 - Prob. 107ECh. 6.10 - Prob. 108ECh. 6.10 - Arc length Use the result of Exercise 108 to find...Ch. 6.10 - Prob. 110ECh. 6.10 - Prob. 111ECh. 6.10 - Definitions of hyperbolic sine and cosine Complete...Ch. 6 - Explain why or why not Determine whether the...Ch. 6 - Displacement from velocity The velocity of an...Ch. 6 - Position, displacement, and distance A projectile...Ch. 6 - Deceleration At t = 0, a car begins decelerating...Ch. 6 - An oscillator The acceleration of an object moving...Ch. 6 - A race Starting at the same point on a straight...Ch. 6 - Fuel consumption A small plane in flight consumes...Ch. 6 - Variable flow rate Water flows out of a tank at a...Ch. 6 - Decreasing velocity A projectile is fired upward,...Ch. 6 - Decreasing velocity A projectile is fired upward,...Ch. 6 - An exponential bike ride Tom and Sue took a bike...Ch. 6 - Prob. 12RECh. 6 - Areas of regions Use any method to find the area...Ch. 6 - Prob. 14RECh. 6 - Prob. 15RECh. 6 - Prob. 16RECh. 6 - Areas of regions Use any method to find the area...Ch. 6 - Areas of regions Use any method to find the area...Ch. 6 - Areas of regions Use any method to find the area...Ch. 6 - Prob. 20RECh. 6 - Prob. 21RECh. 6 - Two methods The region R in the first quadrant...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Area and volume The region R is bounded by the...Ch. 6 - Comparing volumes Let R be the region bounded by y...Ch. 6 - Multiple regions Determine the area of the region...Ch. 6 - Prob. 39RECh. 6 - Arc length Find the length of the following...Ch. 6 - Prob. 41RECh. 6 - Arc length Find the length of the following...Ch. 6 - Arc length Find the length of the following...Ch. 6 - Arc length Find the length of the following...Ch. 6 - Prob. 45RECh. 6 - Surface area and volume Let f(x)=13x3 and let R be...Ch. 6 - Surface area and volume Let f(x)=3xx2 and let R be...Ch. 6 - Surface area of a cone Find the surface area of a...Ch. 6 - Surface area and more Let f(x)=x42+116x2 and let R...Ch. 6 - Variable density in one dimension Find the mass of...Ch. 6 - Variable density in one dimension Find the mass of...Ch. 6 - Variable density in one dimension Find the mass of...Ch. 6 - Spring work a. It lakes 50 J of work to stretch a...Ch. 6 - Pumping water A cylindrical water tank has a...Ch. 6 - Force on a dam Find the total force on the face of...Ch. 6 - Integrals Evaluate the following integrals. 56....Ch. 6 - Integrals Evaluate the following integrals. 57....Ch. 6 - Integrals Evaluate the following integrals. 58....Ch. 6 - Integrals Evaluate the following integrals. 59....Ch. 6 - Integrals Evaluate the following integrals. 60....Ch. 6 - Integrals Evaluate the following integrals. 61....Ch. 6 - Integrals Evaluate the following integrals. 62....Ch. 6 - Integrals Evaluate the following integrals. 63....Ch. 6 - Radioactive decay The mass of radioactive material...Ch. 6 - Population growth Growing from an initial...Ch. 6 - Prob. 66RECh. 6 - Prob. 67RECh. 6 - Prob. 68RECh. 6 - Prob. 69RECh. 6 - Equal area property for parabolas Let f(x) = ax2 +...Ch. 6 - Derivatives of hyperbolic functions Compute the...Ch. 6 - Prob. 72RECh. 6 - Linear approximation Find the linear approximation...Ch. 6 - Limit Evaluate limx(tanhx)x.

Additional Engineering Textbook Solutions

Find more solutions based on key concepts
76. Dew Point and Altitude The dew point decreases as altitude increases. If the dew point on the ground is 80°...

College Algebra with Modeling & Visualization (5th Edition)

1. Verifying Requirements In the largest clinical trial ever conducted, 401,974 children were randomly assigned...

Elementary Statistics (13th Edition)

Each of Exercises 1–6 gives a formula for the nth term an of a sequence {an}. Find the values of a1 a2, a3 and ...

University Calculus: Early Transcendentals (4th Edition)

Write a sentence that illustrates the use of 78 in each of the following ways. a. As a division problem. b. As ...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

Matching In Exercises 17–20, match the level of confidence c with the appropriate confidence interval. Assume e...

Elementary Statistics: Picturing the World (7th Edition)

In Problems 25-32, the graph of a function is given. Use the graph to find: a. The intercepts, if any b. The do...

Precalculus

Knowledge Booster
Background pattern image
Computer Science
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
The surface area and volume of cone, cylinder, prism and pyramid; Author: AtHome Tuition;https://www.youtube.com/watch?v=SlaQmaJCOt8;License: Standard YouTube License, CC-BY