Chapter 6.2, Problem 66E

Equal area properties for parabolas Consider the parabola y = x². Let P, Q, and R be points on the parabola with R between P and Q on the curve. Let ℓ_P, ℓ_Q, and ℓ_R be the lines tangent to the parabola at P, Q, and R, respectively (see figure). Let P′ be the intersection point of ℓ_Q and ℓ_R, let Q′ be the intersection point of ℓ_P and ℓ_R, and let R′ be the intersection point of ℓ_P and ℓ_Q. Prove that Area ΔPQR = 2 · Area ΔP′Q′R′ in the following cases. (In fact, the property holds for any three points on any parabola.) (Source: Mathematics Magazine 81, 2, Apr 2008)

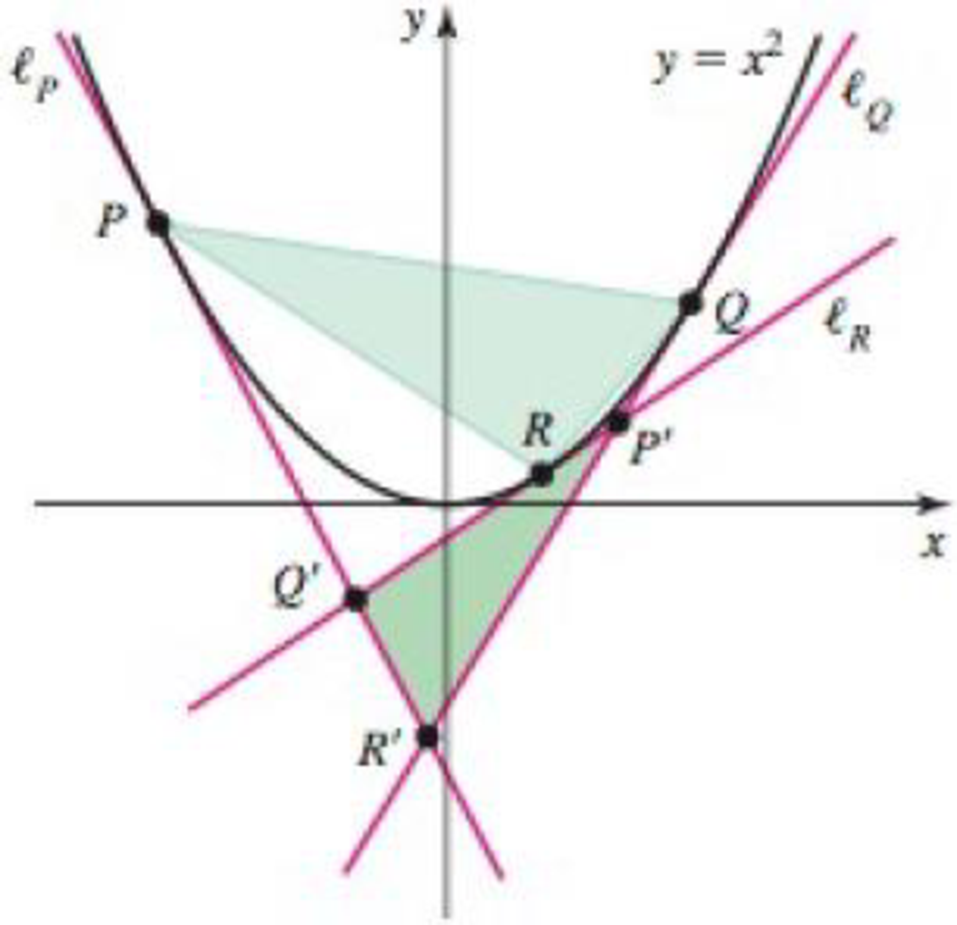
1. a. P(−a, a²), Q(a, a²), and R(0, 0), where a is a positive real number
2. b. P(−a, a²), Q(b, b²), and R(0, 0), where a and b are positive real numbers
3. c. P(−a, a²), Q(b, b²), and R is any point between P and Q on the curve