
Concept explainers
Power and energy Power and energy are often used interchangeably, but they are quite different. Energy is what makes matter move or heat up and is measured in units of joules (J) or Calories (Cal), where 1 Cal = 4184 J. One hour of walking consumes roughly 106 J, or 250 Cal. On the other hand, power is the rate at which energy is used and is measured in watts (W; 1 W = 1 J/s). Other useful units of power are kilowatts (1 kW = 103 W) and megawatts (1 MW = 106 W). If energy is used at a rate of 1 kW for 1 hr, the total amount of energy used is 1 kilowatt-hour (kWh), which is 3.6 × 106 J.
Suppose the power function of a large city over a 24-hr period is given by
where P is measured in megawatts and t = 0 corresponds to 6:00 P.M. (see figure).
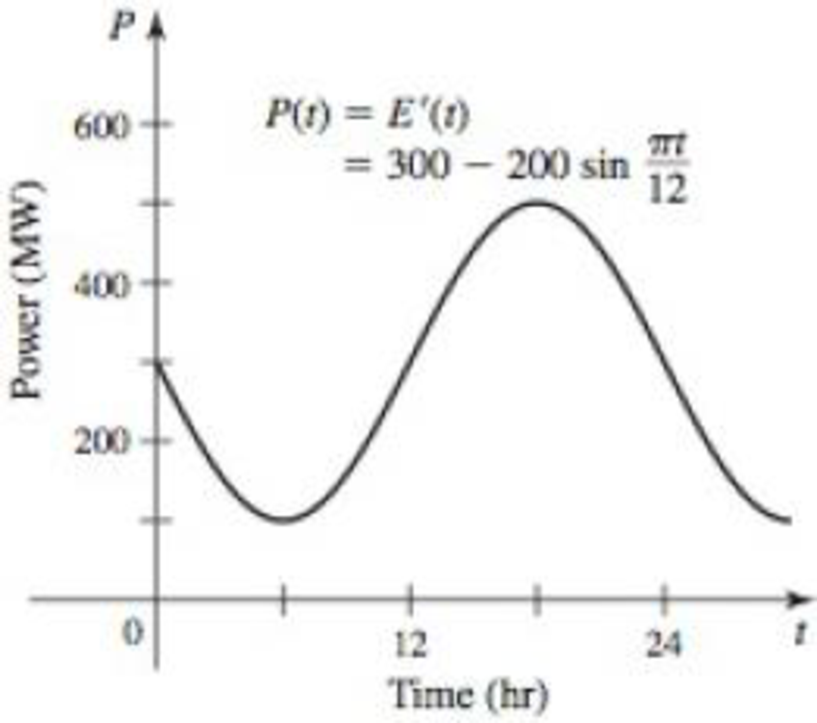
- a. How much energy is consumed by this city in a typical 24-hr period? Express the answer in megawatt-hours and in joules.
- b. Burning 1 kg of coal produces about 450 kWh of energy. How many kg of coal are required to meet the energy needs of the city for 1 day? For 1 year?
- c. Fission of 1 g of uranium-235 (U-235) produces about 16,000 kWh of energy. How many grams of uranium are needed to meet the energy needs of the city for 1 day? For 1 year?
- d. A typical wind turbine can generate electrical power at a rate of about 200 kW. Approximately how many wind turbines are needed to meet the average energy needs of the city?
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
CODE/CALC ET 3-HOLE
Additional Engineering Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Algebra and Trigonometry (6th Edition)
Pre-Algebra Student Edition
Elementary Statistics (13th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- Example: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardExample: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardPlease can you give detailed steps on how the solutions change from complex form to real form. Thanks.arrow_forward
- Examples: Solve the following differential equation using Laplace transform (e) ty"-ty+y=0 with y(0) = 0, and y'(0) = 1arrow_forwardExamples: Solve the following differential equation using Laplace transform (a) y" +2y+y=t with y(0) = 0, and y'(0) = 1arrow_forwardπ 25. If lies in the interval <0arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning





