Chapter 6.6, Problem 91SR

To determine

A rectangle is inscribed in an isosceles triangle as shown. Find the dimensions of the inscribed rectangle with maximum area.

Answer to Problem 91SR

The dimensions of the rectangle when its area is maximum are 5 inches and 4 inches.

Explanation of Solution

Given:

The diagram is :

  

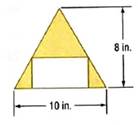
Concept Used:

• To maximize a function f ( x ), take its derivative wrt x and equate it to 0:

  $\frac{d}{dx}\left[f(x)\right]=0$ and find the value of x .

If $\frac{d^2}{d{x}^2}\left[f(x)\right]<0$ , then the value is maximum.

Calculation:

In the given triangle, let

2b = length of the base of the triangle = 10 in.

h = height of the triangle = 8 in.

In the given rectangle , let

2x = length of the base adjacent to the base of the triangle

y = width of the rectangle

  

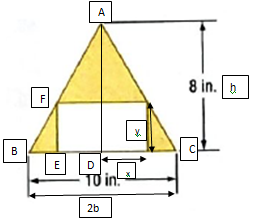
The triangles $\Delta ABD$ and $\Delta FBE$ are similar .

So, $\begin{array}{l}\frac{AD}{FE}=\frac{BD}{BE}\\ \Rightarrow \frac{h}{y}=\frac{b}{b-x}\\ \Rightarrow h(b-x)=by\mathrm{..................}[\text{multiply each side by y(b-x)]}\\ \Rightarrow y=\frac{h(b-x)}{b}\mathrm{..................}[\text{divide each side by b]}\\ \Rightarrow y=h-\frac{hx}{b}\end{array}$

The area of the rectangle is:

  $\begin{array}{l}length\times width\\ =2x\cdot y\\ =2x\cdot \left(h-\frac{hx}{b}\right)\mathrm{......................}[y=h-\frac{hx}{b}]\\ =2xh-\frac{2h{x}^2}{b}\\ \Rightarrow a(x)=2xh-\frac{2h{x}^2}{b}\end{array}$

Now, we need to maximize the area of the rectangle . So, we will derivative the function that represents the area of the rectangle wrt x and equate it to 0:

  $\begin{array}{l}\frac{d}{dx}\left[a(x)\right]=0\\ \Rightarrow \frac{d}{dx}\left[2xh-\frac{2h{x}^2}{b}\right]=0\\ \Rightarrow 2h-\frac{4hx}{b}=\mathrm{0..................}[\text{since }\frac{d^2}{d{x}^2}(a(x))=-\frac{4h}{b}<0,\text{the solution is a point of maxima]}\\ \Rightarrow 2hb-4hx=\mathrm{0................}[\text{multiply both sides by b]}\\ \Rightarrow 2hb=4hx\mathrm{.....................}[\text{add 4hx each side]}\\ \Rightarrow \frac{4hx}{2h}=\frac{2hb}{2h}\mathrm{...................}[\text{divide each side by 2h]}\\ \Rightarrow 2x=b\\ \Rightarrow x=\frac{b}{2}\mathrm{...........................}[\text{divide each side by 2]}\\ and\\ y=h-\frac{hx}{b}\\ \Rightarrow y=h-\frac{h}{b}\cdot \left(\frac{b}{2}\right)\mathrm{............}[x=\frac{b}{2}]\\ \Rightarrow y=h-\frac{h}{2}\\ \Rightarrow y=\frac{h}{2}\end{array}$

Hence,

The length of the rectangle = $2x=2\cdot \left(\frac{b}{2}\right)=b=\frac{10}{2}=5$ inches.

The width of the rectangle = $y=\frac{h}{2}=\frac{8}{2}=4$ inches.

So, the dimensions of the rectangle when its area is maximum are 5 inches and 4 inches.