Chapter 6.3, Problem 62SR

(a)

To determine

To Graph:

The given equation for the years 1985 to 2005

Explanation of Solution

Given:

The number of households in the United States with cable TV after 1985 can be modeled by the function $C(t)=-43.2t^2+1343t+790$ , where t represents the number of years since 1985.

Calculation:

Number of years from 1985 to 2005 = 2005-1985 = 20 years

Let x -axis represent the number of years since 1985 and y -axis represent the number of households in the United States with cable TV after 1985.

Represent the equation $C(t)=-43.2t^2+1343t+790$ in the graph:

  

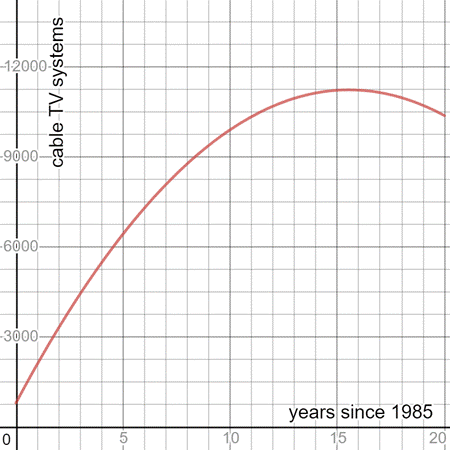
(b)

To determine

The turning points of the graph and its end behavior.

Answer to Problem 62SR

Turning point between t = 15 and 16

End behaviour:

  $\begin{array}{l}C(t)\to -\infty \text{ as t}\to \text{ -}\infty \\ \text{and }\\ \text{C(t)}\to -\infty \text{ as t}\to \text{+}\infty \end{array}$

Explanation of Solution

Given:

The number of households in the United States with cable TV after 1985 can be modeled by the function $C(t)=-43.2t^2+1343t+790$ , where t represents the number of years since 1985.

Calculation:

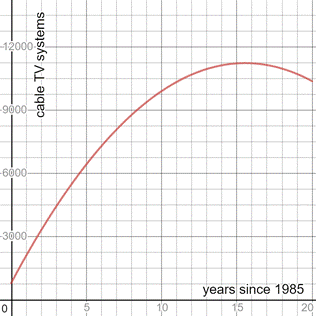
From the graph in part (a) :

The graph has one turning point between :

t = 15 and 16 . The graph has related maxima at this point.

The end behaviour of the graph :

  $\begin{array}{l}C(t)\to -\infty \text{ as t}\to \text{ -}\infty \\ \text{and }\\ \text{C(t)}\to -\infty \text{ as t}\to \text{+}\infty \end{array}$

(c)

To determine

To Find:

The domain of the function and eliminate the range of the function.

Answer to Problem 62SR

Domain = all real numbers

  $Range=\left\{y\right|y\le 11,225\}$

Explanation of Solution

Given:

Graph of the equation $C(t)=-43.2t^2+1343t+790$ from part (a):

  

Calculation:

From the equation $C(t)=-43.2t^2+1343t+790$ , since it is defined for all values of t , so the domain is all real numbers.

The graph takes all the y -values less than or equal to 11,225.

So, the $Range=\left\{y\right|y\le 11,225\}$

(d)

To determine

To Find:

What trends in households with cable TV does the graph suggest? Is it reasonable to assume that the trend will continue indefinitely?

Answer to Problem 62SR

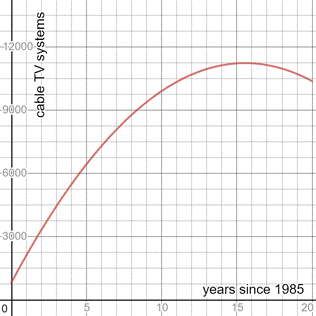
The number of cable TV systems rose steadily from 1985 to 2000 , then it started to decline.

The trend will not continue indefinitely.

Explanation of Solution

Given:

Graph of the equation $C(t)=-43.2t^2+1343t+790$ from part (a):

  

Calculation:

From the graph , we can observe:

The number of cable TV systems rose steadily from t = 0 to t = 15 . That is , it rose steadily from 1985 to 2000 Then the graph goes down ,so after year 2000, the number of cable TV systems began to decline.

Since the number of cable TV systems cannot be negative. So, the graph cannot go below y=0.

So, the trend may continue for some years, but the number of cable TV systems cannot decline at this rate indefinitely.