
Interpretation:
To plot the nullclines
Concept Introduction:
Nullclines are the curves in the phase portrait where either
Fixed points occur where
The Jacobian matrix at a general point
The Eigenvalue
The solution of the quadratic equation is
The unstable manifold for a fixed point is the set of all points in the plane which tend to the fixed point as time goes to negative infinity.
Answer to Problem 6E
Solution:
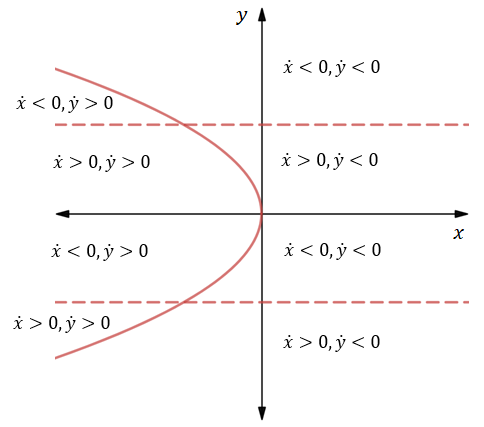
a) The nullclines
b) The sign of
c) The Eigenvalues and Eigenvectors of the saddle points at
d) It is proved that the unstable manifold
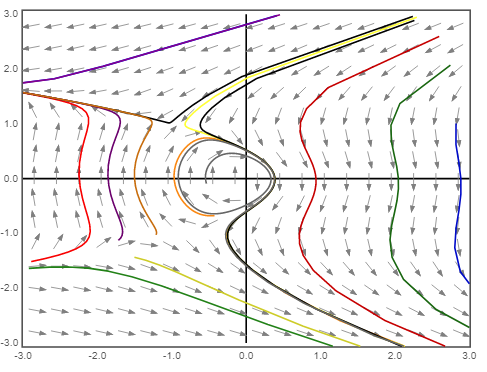
e) The phase portrait for the given system is plotted.
Explanation of Solution
a) The system is given as
Nullclines are the curves in the phase portrait where either
Substituting
Thus,
Substituting
Therefore, the nullclines of the given system are
The nullclines plot for the given system equation is shown below:
b) The value of the system at
The sign of
c) The fixed points of the system would be where
The fixed points can be obtained by substituting
Therefore, the fixed points are
The Jacobian matrix at a general point
Substituting the given system in the Jacobian matrix,
The value of the Jacobian matrix at the fixed point
Therefore, from the Jacobian matrix, it is clear that the fixed point
The value of the Jacobian matrix at the fixed point
The value of the Jacobian matrix at the fixed point
The Eigenvalue
To find the Eigenvalues and the Eigenvectors of the Jacobian matrix
The determinant of the above matrix is
From the above matrix,
The above quadratic equation can be solved by using
Therefore, the Eigenvalue of the Jacobian matrix
The corresponding Eigenvectors for the above Jacobian matrix
Similarly, to find the Eigenvalues and the Eigenvectors of the Jacobian matrix
The determinant of the above matrix is
From the above matrix,
The above quadratic equation can be solved by using
Therefore, the Eigenvalue of the Jacobian matrix
The corresponding Eigenvectors for the above Jacobian matrix
d) The unstable manifold for a fixed point is the set of all points in the plane which tend to the fixed point as time goes to negative infinity.
Consider the unstable manifold of the saddle point
Since the system is reversible under the transformation
e) Consider the unstable manifold of the saddle point
Since the system is reversible under the transformation
The phase portrait of the given system is shown below:
Want to see more full solutions like this?
Chapter 6 Solutions
Nonlinear Dynamics and Chaos
- optimizaton theoryarrow_forwardμ=1 r = 30 mm 500 mm a 7000 mm b 7000 mm C 500 mmarrow_forwardPhil has systematically contributed $3000 to his RRSP at the beginning of every three months for the past 17 years.If the RRSP has earned 8.8% compounded quarterly, what is the value of Phil’s RRSP today? (Do not round intermediate calculations and round your final answer to 2 decimal places.)The value of the RRSP today $arrow_forward
- Answer this pleasearrow_forwardCan you prove that P(a,b) >= P(a',b) for a >= a' >= b >= 0arrow_forwardFigure 1 Simulation structure diagram for a turbine cold-end system. approximated by the two fourth degree polynomial equations as follows: The turbine "cold-and" system generally consists of turbine exhaust and condenser, and cooling tower (Fig. 1). For a 250 MW unit, the turbine performance data with the maximum steam throttle flow can be NHR NEW NHR Turbine and NHR = −45.19(CP)* + 420(CP)® – 1442(CP)2 + 2248(CP) +6666 (a) NKW = 4,883(CP)* – 44,890(CP)3 + 152,600(CP)2 – 231,500(CP) + 383,400. (b) The condenser and mechanical-draft cooling tower have the performance equations, respectively, CP 1.6302-0.50095 x 10-1 (CWT) OP Coupling 1 Condenser CR WFR CWT Coupling 2 WST Cooling Tower CR System Boundary 2 (The circulating water flow is assumed to flow at the rate of 145,000 gpm.) In addition to the given performance equations give above, we also need two coupling equations to complete the mathematical model for this cooling system. The first equation is the coupling between the…arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
