Chapter 6.6, Problem 24E

To determine

To write next three terms of the geometric sequence:

  $\frac{16}{9},\frac{8}{3},4,6,\mathrm{....}$

And also plot the graph of the sequence.

Answer to Problem 24E

The next three terms of given geometric series are: 9, $13.5$ , and $20.25$.

  

Explanation of Solution

Given:

The given geometric sequence is:

  $\frac{16}{9},\frac{8}{3},4,6,\mathrm{....}$

Concept Used:

• In a geometric sequence, the ration between each pair of consecutive terms is the same, this ratio is called the common ratio.
• Each term of a geometric series is found by multiplying the previous term by the common ratio.

Calculation:

To write next three terms of the geometric sequence:

  $\frac{16}{9},\frac{8}{3},4,6,\mathrm{....}$

First find the common ratio of the sequence by dividing second term by first, as

  $\begin{array}{c}\frac{\frac{8}{3}}{\frac{16}{9}}=\frac{8}{3}\times \frac{9}{16}\\ =\frac{3}{2}\\ =1.5\end{array}$

Thus, common ration of the given geometric sequence is $1.5$ , that is, each term of the given geometric series can be found by multiplying the previous term by the common ratio $1.5$.

Thus, next term of 6 will be:

  $6\times 1.5=9$

Similarly, next term of 9 is:

  $9\times 1.5=13.5$

And, next term of $13.5$ is:

  $13.5\times 1.5=20.25$

Thus, next three terms of given geometric series are: 9, $13.5$ , and $20.25$.

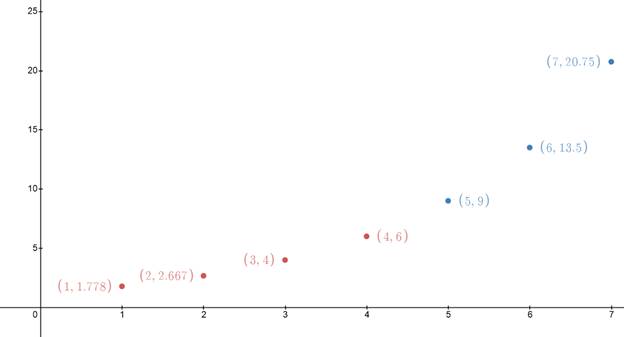
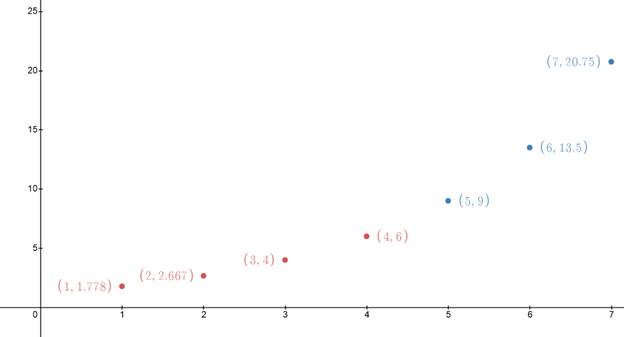
Now, to plot the graph of given sequence, first make a table of representing terms, say $a_n$ , of the sequence and their respectively place, n , from the above information as:

n	1	2	3	4	5	6	7
$a_n$	$\frac{16}{9}$	$\frac{8}{3}$	4	6	9	13.5	$20.25$

Now, using this table plot the graph of the given sequence by plotting the coordinates in above table: $\left(1,\frac{16}{9}\right),\left(2,\frac{8}{3}\right),\left(3,4\right),\left(4,6\right),\left(5,9\right),\left(6,13.5\right),\left(7,20.25\right)$.

Thus, graph of the sequence is represented by blue and red dots, as