Chapter 6, Problem 17CT

a.

To determine

To Identify: The Initial amount, decay factor and decay rate.

Answer to Problem 17CT

Initial amount =1

Decay factor=0.99988

Decay rate=0.012%

Explanation of Solution

Given information: The equation $P={(0.99988)}^a$

Formula used: $P=A{(1-r)}^x$ . Where ‘A’ is initial amount, (1 - r) is decay factor and ‘r’ is decay rate in percent.

Calculation:

Let’s compare the given equation with formula.

Initial amount A=1

Decay factor $1-r=0.99988$

To find decay rate, let’s solve $1-r=0.99988$ for ‘r’.

Subtract both sides 1.

  $-r=-0.00012$

Divide both sides by -1.

  $r=0.00012$

Multiply it by 100% to get decay rate in percent.

  $\text{Decay rate}=0.00012(100\%)=0.012\%$

b.

To determine

To find: Pressure at an altitude of 5000 feet.

Answer to Problem 17CT

Pressure is 0.833 atmosphere.

Explanation of Solution

Given information: Graph the function using graphing calculator and find the P when a =1524 feet.

Calculation:

Let’s graph using online graphing calculator.

Before graph it, it needed to change 5000 feet to meters. Because our ‘a’ represents in meters.

1 meter = 3.28084 foot

So, 5000 feet could be found by dividing 5000 by 3.28084.

So, 5000 feet = 1524 meters

  

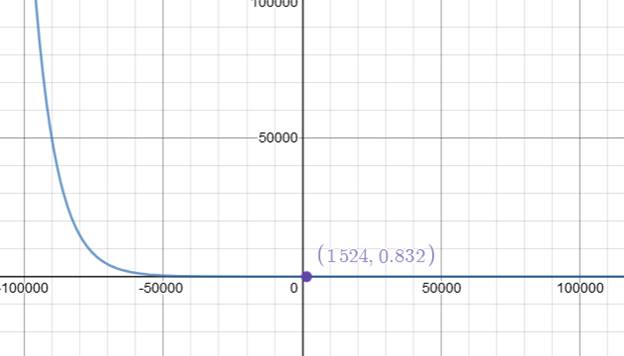
Interpretation: The pressure is 0.833 atmospheres approximately when altitude is 5000 feet(1524 meters).