
Concept explainers
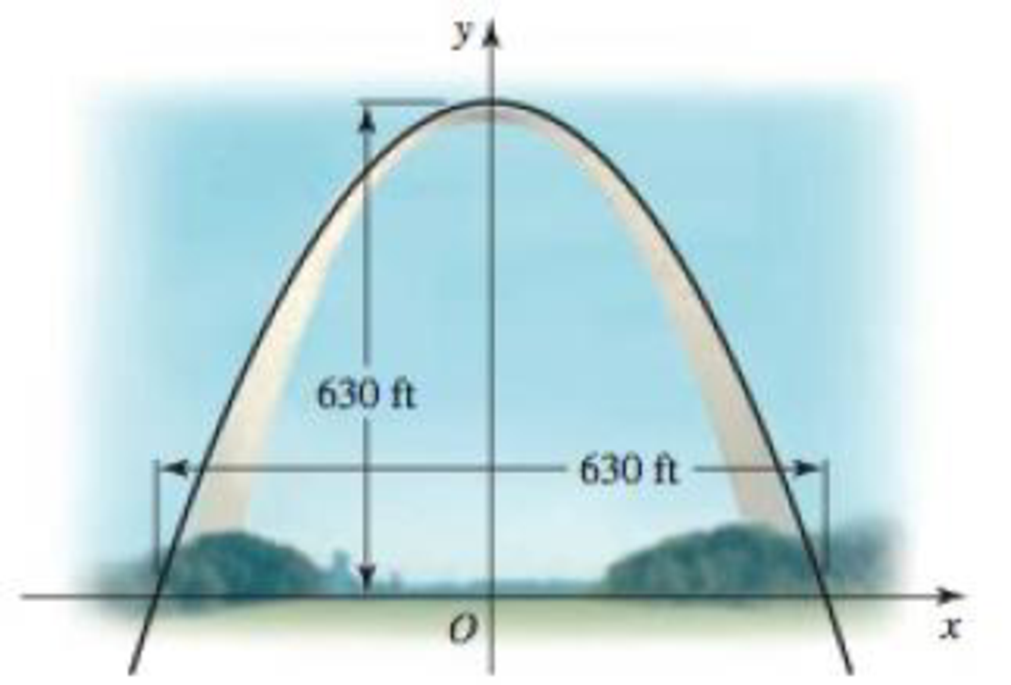
Gateway Arch The shape of the Gateway Arch in St. Louis (with a height and a base length of 630 ft) is modeled by the function y = −630 cosh (x/239.2) + 1260, where |x| ≤ 315, and x and y are measured in feet (see figure). The function cosh x is the hyperbolic cosine, defined by
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Single Variable Calculus: Early Transcendentals & Student Solutions Manual, Single Variable for Calculus: Early Transcendentals & MyLab Math -- Valuepack Access Card Package
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
A First Course in Probability (10th Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Elementary Statistics: Picturing the World (7th Edition)
College Algebra with Modeling & Visualization (5th Edition)
- the correct answer is C could you please explainarrow_forwardWhich of the functions shown below is differentiable at z = 2? Select the correct answer below: о -7-6-5-4-3-2- −7 −6 −5 −4 −3-2 1 2 4 5 6 -7-6-5-4-3-2- -7-6-5-4-3 2 45arrow_forwardQuestion Given the graph of f(z) below, find the graph of the derivative of f(z). Select the correct answer below: ° ° 129 -7-6-5-4-3-2 -7-6-5-4-3-2-1123456 ° ° °arrow_forward
- Question Find the open interval(s) of f(x), graph given below, where f'(x) is negative. -3-2-1 1 2 4 5 6 Give your answer in interval notation. For example, (2, 4) U (6,∞). Provide your answer below:arrow_forwardthe correct answer is Ccould you please show me how to do it using the residue theoremarrow_forwardUse the information to find and compare Δy and dy. (Round your answers to four decimal places.) y = x4 + 7 x = −3 Δx = dx = 0.01 Δy = dy =arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
