The Heart of Mathematics: An Invitation to Effective Thinking
4th Edition
ISBN: 9781118156599
Author: Edward B. Burger, Michael Starbird
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.4, Problem 22MS
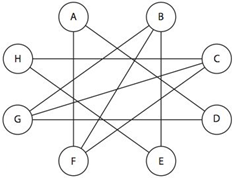
Hunt for Hamilton (S). A large island country has all its cities on the coast. All the airline routes between cities fly over the interior of the island. The graph shows the cities as vertices and the airline routes as edges. Can you find a Hamiltonian circuit in this graph? Why or why not?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Section 2.2 Subsets
71
Exercise Set 2.2
Practice Exercises
In Exercises 1-18, write or in each blank so that the resulting
statement is true.
1. {1, 2, 5}
{1, 2, 3, 4, 5, 6, 7}
2. {2, 3, 7}
{1, 2, 3, 4, 5, 6, 7}
3. {-3, 0, 3}
{-4,-3,-1, 1, 3, 4}
4. {-4, 0, 4}
5. {Monday, Friday}
{-3, -1, 1, 3}
{Saturday, Sunday, Monday, Tuesday, Wednesday}
6. {Mercury, Venus, Earth}
{Venus, Earth, Mars, Jupiter}
7. {x/x is a cat}
{xx is a black cat}
{x|x is a pure-bred dog}
ibrary
mbers,
ause the
entire
sual
8. {xx is a dog}
9. (c, o, n, v, e, r, s, a, t, i, o, n}
{v, o, i, c, e, s, r, a, n, t, o, n}
10. [r, e, v, o, l, u, t, i, o, n}
{t, o, l, o, v, e, r, u, i, n}
33. A = {x|x E N
and
5 < x < 12}
B
=
{x|x E N
and
2 ≤ x ≤ 11}
A_ B
34. A =
{x|x = N
and
3 < x < 10}
B =
A.
{x|x = N
and
2 ≤ x ≤ 8}
B
35. Ø
{7, 8, 9,..., 100}
36. Ø
_{101, 102, 103, . . ., 200}
37. [7, 8, 9,...}
38. [101, 102, 103, ...}
39. Ø
40. { }
{ }
e
In Exercises 41-54, determine whether each statement is true or
false. If…
A truck loaded with rocks weighs 14,260 lb. If the truck weighs 8420 lb, how much do the rocks weigh?
Find the lengths of r, s, t, and u shown in the figure below if r+s=34. Round your answers to the nearest tenth.
Note that the figure is not drawn to scale.
16
37°
r =
S
u =
t
S
u
24
☑
Chapter 6 Solutions
The Heart of Mathematics: An Invitation to Effective Thinking
Ch. 6.1 - Map maker, map maker make me a graph. Represent...Ch. 6.1 - Unabridged list. Represent cach landmass from...Ch. 6.1 - Will the walk work? Does your graph from...Ch. 6.1 - Walk around the house. Is it possibel to traverse...Ch. 6.1 - Walk the line. Does this graph above have an Euler...Ch. 6.1 - Walkabout. Does this graph have an Euler circuit?...Ch. 6.1 - Linking the loops. In this map, the following...Ch. 6.1 - Scenic drive. (S) Here is a map of Rockystone...Ch. 6.1 - Under-edged. (H) Does this graph have an Euler...Ch. 6.1 - No man is an island. The country of Pelago...
Ch. 6.1 - Path-o-rama. For each graph below, determine if...Ch. 6.1 - Walk around the block. Create a graph of the...Ch. 6.1 - Walking the dogs. Your dogs, Abbey and Bear, love...Ch. 6.1 - Delivery query. The next time you see a postal...Ch. 6.1 - Snow job. (ExH) Shown here is a map of the tiny...Ch. 6.1 - Special delivery. (ExH) Julia is the letter...Ch. 6.1 - Draw this old house. Suppose you wanted to trace...Ch. 6.1 - Path of no return. Consider this map showing a...Ch. 6.1 - Without a trace. Is it possibel to trace out...Ch. 6.1 - New Euler. In the three previous Mindscapes, you...Ch. 6.1 - New edge—new circuit. Look at the graph for...Ch. 6.1 - New edge—new path. Review your work for...Ch. 6.1 - Path to proof. Suppose you have a connected graph...Ch. 6.1 - No Euler no how. Look at graph (a) for Mindscape...Ch. 6.1 - Degree day. (S) For cach graph below, determine...Ch. 6.1 - degrees of proof. Review your work for Mindscape...Ch. 6.1 - Degrees in sequence. Can you draw a graph that has...Ch. 6.1 - Even Steven. Review your work in Mindscape 28 to...Ch. 6.1 - Little League lesson. (H) You are in charge of...Ch. 6.1 - With a group of folks. In a small group, discuss...Ch. 6.1 - Power beyond the mathematics. Provide several...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.2 - What a character! What expression gives the Euler...Ch. 6.2 - Count, then verify. What are the values of V, E,...Ch. 6.2 - Sneeze, then verify. Look at an unopened tissue...Ch. 6.2 - Blow, then verify. Inflate a ballon and use a...Ch. 6.2 - Add one. Find the values V, E, and F for the graph...Ch. 6.2 - Bowling. What is the Euler Characteristic of the...Ch. 6.2 - Making change. We begin with the graph pictured at...Ch. 6.2 - Making a point. Take a connected graph and add a...Ch. 6.2 - On the edge (H). Is it possible to add an edge to...Ch. 6.2 - Soap films. Consider the following sequence of...Ch. 6.2 - Dualing. What is the relationship between the...Ch. 6.2 - Prob. 12MSCh. 6.2 - Lots of separation. Suppose we are told that a...Ch. 6.2 - Prob. 14MSCh. 6.2 - Psychic readings. Someone is thinking of a...Ch. 6.2 - Prob. 16MSCh. 6.2 - Prob. 17MSCh. 6.2 - Circular reasoning. Create a connected graph as...Ch. 6.2 - Prob. 19MSCh. 6.2 - More circles. Consider the sphere described in...Ch. 6.2 - In the rough (S). Count the number of facets,...Ch. 6.2 - Cutting corners (H). The following collection of...Ch. 6.2 - Stellar. The following collection of pictures...Ch. 6.2 - A torus graph (ExH). The Euler Characteristic...Ch. 6.2 - Regular unfolding. Each graph below represents...Ch. 6.2 - A tale of two graphs. Suppose we draw a graph that...Ch. 6.2 - Two graph conjectures (S). Can you conjecture a...Ch. 6.2 - Lots of graphs conjecture. Can you conjecture a...Ch. 6.2 - Torus count. Three hollowed, triangular prisms...Ch. 6.2 - Torus two count (H). Carefully count the number of...Ch. 6.2 - Torus many count. Using the preceding calculations...Ch. 6.2 - Prob. 32MSCh. 6.2 - Tell the truth. Someone said that she made a...Ch. 6.2 - No sphere. Suppose we have a sphere built out of...Ch. 6.2 - Soccer ball. A soccer ball is made of pentagons...Ch. 6.2 - Klein bottle. Using the diagram here for building...Ch. 6.2 - Not many neighbors. Show that every map has at...Ch. 6.2 - Infinite edges. Suppose we consider a conn ected...Ch. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.2 - Prob. 44MSCh. 6.2 - Prob. 45MSCh. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.3 - Dont be cross. Here is a drawing of a graph with...Ch. 6.3 - De Plane! De Plane! (S) Is the graph given in...Ch. 6.3 - Countdown (H). For the graph drawing shown, count...Ch. 6.3 - Prob. 4MSCh. 6.3 - Criss-Cross. Is it possible to redraw the graph...Ch. 6.3 - Dont cross in the edge. Each of the graphs drawn...Ch. 6.3 - Hot crossed buns. Each of the graphs drawn below...Ch. 6.3 - Prob. 8MSCh. 6.3 - Spider on a mirror. Is it possible to redraw the...Ch. 6.3 - One more vertex. The graph here is drawn to show...Ch. 6.3 - Yet one more vertex (H). The graph shown is drawn...Ch. 6.3 - Familiar freckles. Is it possible to redraw the...Ch. 6.3 - Remind you of anyone you know? Is it possible to...Ch. 6.3 - Final countdown. For this graph drawing, count the...Ch. 6.3 - Euler check-up. Use your answer to the previous...Ch. 6.3 - Euler second opinion. For the graph drawing shown...Ch. 6.3 - Prob. 17MSCh. 6.3 - Prob. 18MSCh. 6.3 - A colorful museum. This figure shows the floor...Ch. 6.3 - Limit of 5. Start drawing a planar graph. Keep...Ch. 6.3 - Starring the hexagon. Is it possible to redraw...Ch. 6.3 - Prob. 22MSCh. 6.3 - Prob. 23MSCh. 6.3 - Getting greedy. (H) Suppose you are asked to color...Ch. 6.3 - Stingy rather than greedy. By coloring the...Ch. 6.3 - Getting more colorful. Graphs dont have to be...Ch. 6.3 - Prob. 27MSCh. 6.3 - Prob. 28MSCh. 6.3 - Chromatically applied. There are eight radio...Ch. 6.3 - Prob. 30MSCh. 6.3 - Personal perspectives. Write a short essay...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Prob. 37MSCh. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.4 - Up close and personal. Create a graph to model...Ch. 6.4 - Network lookout. Find an examle of a network...Ch. 6.4 - Prob. 3MSCh. 6.4 - Hamiltonian holiday (S). You are interning for a...Ch. 6.4 - Home style. Create a graph to model the rooms in...Ch. 6.4 - Six degrees or less. Suppose this graph is a model...Ch. 6.4 - Degrees of you. Find ten willing friends or...Ch. 6.4 - Campus shortcut. Find a map of your campus and...Ch. 6.4 - Arborist lesson. Which of the graphs below are...Ch. 6.4 - Prob. 10MSCh. 6.4 - Prob. 11MSCh. 6.4 - Prob. 12MSCh. 6.4 - Prob. 13MSCh. 6.4 - Prob. 14MSCh. 6.4 - Prob. 15MSCh. 6.4 - Hamilton Study. Look at the graph you drew to...Ch. 6.4 - Business trip redux. Look back in the section and...Ch. 6.4 - Handling Hamiltons. For each graph below, find a...Ch. 6.4 - Road trip. You are checking out gradua te programs...Ch. 6.4 - Back to Hatties trip. Look back in this section...Ch. 6.4 - Solve the Icosian Game. Find a Hamiltonian circuit...Ch. 6.4 - Hunt for Hamilton (S). A large island country has...Ch. 6.4 - Has no Hamilton. Give some characteristics that...Ch. 6.4 - Cubing Hamilton (ExH). Can you find a Hamihonian...Ch. 6.4 - Hamiltonian path. A Hamiltonian path is a path in...Ch. 6.4 - Sorry, no path. Give some characteristics that...Ch. 6.4 - Prob. 27MSCh. 6.4 - Prob. 28MSCh. 6.4 - Prob. 29MSCh. 6.4 - Prob. 30MSCh. 6.4 - Edge count. Look at all the trees you drew in the...Ch. 6.4 - Personal perspecthes. Write a short essay...Ch. 6.4 - Prob. 33MSCh. 6.4 - Prob. 34MSCh. 6.4 - Dollars and cents. Your spanning tree has three...Ch. 6.4 - Adding up. Your spanning tree has four edges with...Ch. 6.4 - Prob. 38MSCh. 6.4 - Vertex search (H). Your graph has a Hamiltonian...Ch. 6.4 - Binary gossip tree. You told a secret to two of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...
Basic Business Statistics, Student Value Edition
CHECK POINT 1 In a survey on musical tastes, respondents were asked: Do you listed to classical music? Do you l...
Thinking Mathematically (6th Edition)
For any sequence of events E1,E2,..., define a new sequence F1,F2,... of disjoint events (that is. events such ...
A First Course in Probability (10th Edition)
Fill in each blanks so that the resulting statement is true. Any set of ordered pairs is called a/an _______. T...
College Algebra (7th Edition)
Show that the mean, variance, and mgf of the uniform distribution are as given in this section. Also verify tha...
Probability And Statistical Inference (10th Edition)
Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...
College Algebra with Modeling & Visualization (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Find the lengths of w, x, y, and z shown in the figure below if xy=69. Round your answers to the nearest tenth. Note that the figure is not drawn to scale. w= x= z= 16 37° W 24 Х Zarrow_forwardIn each of Problems 1 through 4, draw a direction field for the given differential equation. Based on the direction field, determine the behavior of y as t → ∞. If this behavior depends on the initial value of y at t = 0, describe the dependency.1. y′ = 3 − 2yarrow_forwardA = 5.8271 ± 0.1497 = B 1.77872 ± 0.01133 C=0.57729 ± 0.00908 1. Find the relative uncertainty of A, B, and C 2. Find A-3 3. Find 7B 4. Find A + B 5. Find A B-B - 6. Find A * B 7. Find C/B 8. Find 3/A 9. Find A 0.3B - 10. Find C/T 11. Find 1/√A 12. Find AB²arrow_forward
- B 2- The figure gives four points and some corresponding rays in the xy-plane. Which of the following is true? A B Angle COB is in standard position with initial ray OB and terminal ray OC. Angle COB is in standard position with initial ray OC and terminal ray OB. C Angle DOB is in standard position with initial ray OB and terminal ray OD. D Angle DOB is in standard position with initial ray OD and terminal ray OB.arrow_forwardtemperature in degrees Fahrenheit, n hours since midnight. 5. The temperature was recorded at several times during the day. Function T gives the Here is a graph for this function. To 29uis a. Describe the overall trend of temperature throughout the day. temperature (Fahrenheit) 40 50 50 60 60 70 5 10 15 20 25 time of day b. Based on the graph, did the temperature change more quickly between 10:00 a.m. and noon, or between 8:00 p.m. and 10:00 p.m.? Explain how you know. (From Unit 4, Lesson 7.) 6. Explain why this graph does not represent a function. (From Unit 4, Lesson 8.)arrow_forwardMake up two polynomial functions, f(x) and g(x). • f(x) should be of degree 3 or higher. g(x) should be of degree 4 or higher. • Find f(3) in each of the three ways: substitution, remainder theorem (synthetic division), and long division. You should get the same answer three times for f(3). Find g(-2) once using your choice of the three methods.arrow_forward
- ere are many real-world situations that exhibit exponential and logarithmic nctions. • Describe two real world scenarios, one exponential and one logarithmic. Do not identify yet whether your scenarios are logarithmic or exponential.arrow_forwardLauris Online Back to Subject 不 4 ப 12 2 points T 35° 25° R M 4 N P 6Q 5 What is m/MNT? 120 T 12 What is the length of MR? 120 units 167:02:04 Time Remaining Yama is designing a company logo. The company president requested for the logo to be made of triangles. Yama is proposing the design shown. C 64°F Clear Q Search L 13 Ide dia des You scre Edi 12 L Tarrow_forwardstacie is a resident at a medical facility you work at. You are asked to chart the amount of solid food that she consumes.For the noon meal today, she ate 1/2 of a 3 ounce serving of meatloaf, 3/4 of her 3 ounce serving of mashed potatoes, and 1/3 of her 2 ounce serving of green beans. Show in decimal form how many ounces of solid food that Stacie consumedarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY