
The Heart of Mathematics: An Invitation to Effective Thinking
4th Edition
ISBN: 9781118156599
Author: Edward B. Burger, Michael Starbird
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 6.3, Problem 10MS
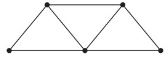
One more vertex. The graph here is drawn to show that it’s planar (there are no edge crossings). Can you add a new vertex v to the graph and draw an edge from v to each of the original vertices without creating any edge crossings? Do it or explain why you can’t.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Suppose that 80% of athletes at a certain college graduate. You randomly select eight athletes. What’s the chance that at most 7 of them graduate?
Suppose that you flip a fair coin four times. What’s the chance of getting at least one head?
Suppose that the chance that an elementary student eats hot lunch is 30 percent. What’s the chance that, among 20 randomly selected students, between 6 and 8 students eat hot lunch (inclusive)?
Chapter 6 Solutions
The Heart of Mathematics: An Invitation to Effective Thinking
Ch. 6.1 - Map maker, map maker make me a graph. Represent...Ch. 6.1 - Unabridged list. Represent cach landmass from...Ch. 6.1 - Will the walk work? Does your graph from...Ch. 6.1 - Walk around the house. Is it possibel to traverse...Ch. 6.1 - Walk the line. Does this graph above have an Euler...Ch. 6.1 - Walkabout. Does this graph have an Euler circuit?...Ch. 6.1 - Linking the loops. In this map, the following...Ch. 6.1 - Scenic drive. (S) Here is a map of Rockystone...Ch. 6.1 - Under-edged. (H) Does this graph have an Euler...Ch. 6.1 - No man is an island. The country of Pelago...
Ch. 6.1 - Path-o-rama. For each graph below, determine if...Ch. 6.1 - Walk around the block. Create a graph of the...Ch. 6.1 - Walking the dogs. Your dogs, Abbey and Bear, love...Ch. 6.1 - Delivery query. The next time you see a postal...Ch. 6.1 - Snow job. (ExH) Shown here is a map of the tiny...Ch. 6.1 - Special delivery. (ExH) Julia is the letter...Ch. 6.1 - Draw this old house. Suppose you wanted to trace...Ch. 6.1 - Path of no return. Consider this map showing a...Ch. 6.1 - Without a trace. Is it possibel to trace out...Ch. 6.1 - New Euler. In the three previous Mindscapes, you...Ch. 6.1 - New edge—new circuit. Look at the graph for...Ch. 6.1 - New edge—new path. Review your work for...Ch. 6.1 - Path to proof. Suppose you have a connected graph...Ch. 6.1 - No Euler no how. Look at graph (a) for Mindscape...Ch. 6.1 - Degree day. (S) For cach graph below, determine...Ch. 6.1 - degrees of proof. Review your work for Mindscape...Ch. 6.1 - Degrees in sequence. Can you draw a graph that has...Ch. 6.1 - Even Steven. Review your work in Mindscape 28 to...Ch. 6.1 - Little League lesson. (H) You are in charge of...Ch. 6.1 - With a group of folks. In a small group, discuss...Ch. 6.1 - Power beyond the mathematics. Provide several...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.1 - Here we celebrate the power of algebra as a...Ch. 6.2 - What a character! What expression gives the Euler...Ch. 6.2 - Count, then verify. What are the values of V, E,...Ch. 6.2 - Sneeze, then verify. Look at an unopened tissue...Ch. 6.2 - Blow, then verify. Inflate a ballon and use a...Ch. 6.2 - Add one. Find the values V, E, and F for the graph...Ch. 6.2 - Bowling. What is the Euler Characteristic of the...Ch. 6.2 - Making change. We begin with the graph pictured at...Ch. 6.2 - Making a point. Take a connected graph and add a...Ch. 6.2 - On the edge (H). Is it possible to add an edge to...Ch. 6.2 - Soap films. Consider the following sequence of...Ch. 6.2 - Dualing. What is the relationship between the...Ch. 6.2 - Prob. 12MSCh. 6.2 - Lots of separation. Suppose we are told that a...Ch. 6.2 - Prob. 14MSCh. 6.2 - Psychic readings. Someone is thinking of a...Ch. 6.2 - Prob. 16MSCh. 6.2 - Prob. 17MSCh. 6.2 - Circular reasoning. Create a connected graph as...Ch. 6.2 - Prob. 19MSCh. 6.2 - More circles. Consider the sphere described in...Ch. 6.2 - In the rough (S). Count the number of facets,...Ch. 6.2 - Cutting corners (H). The following collection of...Ch. 6.2 - Stellar. The following collection of pictures...Ch. 6.2 - A torus graph (ExH). The Euler Characteristic...Ch. 6.2 - Regular unfolding. Each graph below represents...Ch. 6.2 - A tale of two graphs. Suppose we draw a graph that...Ch. 6.2 - Two graph conjectures (S). Can you conjecture a...Ch. 6.2 - Lots of graphs conjecture. Can you conjecture a...Ch. 6.2 - Torus count. Three hollowed, triangular prisms...Ch. 6.2 - Torus two count (H). Carefully count the number of...Ch. 6.2 - Torus many count. Using the preceding calculations...Ch. 6.2 - Prob. 32MSCh. 6.2 - Tell the truth. Someone said that she made a...Ch. 6.2 - No sphere. Suppose we have a sphere built out of...Ch. 6.2 - Soccer ball. A soccer ball is made of pentagons...Ch. 6.2 - Klein bottle. Using the diagram here for building...Ch. 6.2 - Not many neighbors. Show that every map has at...Ch. 6.2 - Infinite edges. Suppose we consider a conn ected...Ch. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.2 - Prob. 44MSCh. 6.2 - Prob. 45MSCh. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.2 - Here we celebrate the power of algebra as a...Ch. 6.3 - Dont be cross. Here is a drawing of a graph with...Ch. 6.3 - De Plane! De Plane! (S) Is the graph given in...Ch. 6.3 - Countdown (H). For the graph drawing shown, count...Ch. 6.3 - Prob. 4MSCh. 6.3 - Criss-Cross. Is it possible to redraw the graph...Ch. 6.3 - Dont cross in the edge. Each of the graphs drawn...Ch. 6.3 - Hot crossed buns. Each of the graphs drawn below...Ch. 6.3 - Prob. 8MSCh. 6.3 - Spider on a mirror. Is it possible to redraw the...Ch. 6.3 - One more vertex. The graph here is drawn to show...Ch. 6.3 - Yet one more vertex (H). The graph shown is drawn...Ch. 6.3 - Familiar freckles. Is it possible to redraw the...Ch. 6.3 - Remind you of anyone you know? Is it possible to...Ch. 6.3 - Final countdown. For this graph drawing, count the...Ch. 6.3 - Euler check-up. Use your answer to the previous...Ch. 6.3 - Euler second opinion. For the graph drawing shown...Ch. 6.3 - Prob. 17MSCh. 6.3 - Prob. 18MSCh. 6.3 - A colorful museum. This figure shows the floor...Ch. 6.3 - Limit of 5. Start drawing a planar graph. Keep...Ch. 6.3 - Starring the hexagon. Is it possible to redraw...Ch. 6.3 - Prob. 22MSCh. 6.3 - Prob. 23MSCh. 6.3 - Getting greedy. (H) Suppose you are asked to color...Ch. 6.3 - Stingy rather than greedy. By coloring the...Ch. 6.3 - Getting more colorful. Graphs dont have to be...Ch. 6.3 - Prob. 27MSCh. 6.3 - Prob. 28MSCh. 6.3 - Chromatically applied. There are eight radio...Ch. 6.3 - Prob. 30MSCh. 6.3 - Personal perspectives. Write a short essay...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Prob. 37MSCh. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.3 - Here we celebrate the power of algebra as a...Ch. 6.4 - Up close and personal. Create a graph to model...Ch. 6.4 - Network lookout. Find an examle of a network...Ch. 6.4 - Prob. 3MSCh. 6.4 - Hamiltonian holiday (S). You are interning for a...Ch. 6.4 - Home style. Create a graph to model the rooms in...Ch. 6.4 - Six degrees or less. Suppose this graph is a model...Ch. 6.4 - Degrees of you. Find ten willing friends or...Ch. 6.4 - Campus shortcut. Find a map of your campus and...Ch. 6.4 - Arborist lesson. Which of the graphs below are...Ch. 6.4 - Prob. 10MSCh. 6.4 - Prob. 11MSCh. 6.4 - Prob. 12MSCh. 6.4 - Prob. 13MSCh. 6.4 - Prob. 14MSCh. 6.4 - Prob. 15MSCh. 6.4 - Hamilton Study. Look at the graph you drew to...Ch. 6.4 - Business trip redux. Look back in the section and...Ch. 6.4 - Handling Hamiltons. For each graph below, find a...Ch. 6.4 - Road trip. You are checking out gradua te programs...Ch. 6.4 - Back to Hatties trip. Look back in this section...Ch. 6.4 - Solve the Icosian Game. Find a Hamiltonian circuit...Ch. 6.4 - Hunt for Hamilton (S). A large island country has...Ch. 6.4 - Has no Hamilton. Give some characteristics that...Ch. 6.4 - Cubing Hamilton (ExH). Can you find a Hamihonian...Ch. 6.4 - Hamiltonian path. A Hamiltonian path is a path in...Ch. 6.4 - Sorry, no path. Give some characteristics that...Ch. 6.4 - Prob. 27MSCh. 6.4 - Prob. 28MSCh. 6.4 - Prob. 29MSCh. 6.4 - Prob. 30MSCh. 6.4 - Edge count. Look at all the trees you drew in the...Ch. 6.4 - Personal perspecthes. Write a short essay...Ch. 6.4 - Prob. 33MSCh. 6.4 - Prob. 34MSCh. 6.4 - Dollars and cents. Your spanning tree has three...Ch. 6.4 - Adding up. Your spanning tree has four edges with...Ch. 6.4 - Prob. 38MSCh. 6.4 - Vertex search (H). Your graph has a Hamiltonian...Ch. 6.4 - Binary gossip tree. You told a secret to two of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. combination of numbers, variables, and operation symbols is called an algebraic______.
Algebra and Trigonometry (6th Edition)
Fill in each blank so that the resulting statement is true.
1. A combination of numbers, variables, and opera...
College Algebra (7th Edition)
In Hamilton County, Ohio, the mean number of days needed to sell a house is 86 days (Cincinnati Multiple Listin...
STATISTICS F/BUSINESS+ECONOMICS-TEXT
The table by using the given graph of h.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Find the volumes of the solids generated by revolving the regions bounded by the lines and curves in Exercises ...
University Calculus: Early Transcendentals (4th Edition)
Consider the following technique for shuffling a deck of n cards: F of any initial ordering of the cards, go th...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Bob’s commuting times to work are varied. He makes it to work on time 80 percent of the time. On 12 randomly selected trips to work, what’s the chance that Bob makes it on time at least 10 times?arrow_forwardYour chance of winning a small prize in a scratch-off ticket is 10 percent. You buy five tickets. What’s the chance you will win at least one prize?arrow_forwardSuppose that 60 percent of families own a pet. You randomly sample four families. What is the chance that two or three of them own a pet?arrow_forward
- If 40 percent of university students purchase their textbooks online, in a random sample of five students, what’s the chance that exactly one of them purchased their textbooks online?arrow_forwardA stoplight is green 40 percent of the time. If you stop at this light eight random times, what is the chance that it’s green exactly five times?arrow_forwardIf 10 percent of the parts made by a certain company are defective and have to be remade, what is the chance that a random sample of four parts has one that is defective?arrow_forward
- Question 4 Fourteen individuals were given a complex puzzle to complete. The times in seconds was recorded for their first and second attempts and the results provided below: 1 2 3 first attempt 172 255 second attempt 70 4 5 114 248 218 194 270 267 66 6 7 230 219 341 174 8 10 9 210 261 347 218 200 281 199 308 268 243 236 300 11 12 13 14 140 302 a. Calculate a 95% confidence interval for the mean time taken by each individual to complete the (i) first attempt and (ii) second attempt. [la] b. Test the hypothesis that the difference between the two mean times for both is 100 seconds. Use the 5% level of significance. c. Subsequently, it was learnt that the times for the second attempt were incorrecly recorded and that each of the values is 50 seconds too large. What, if any, difference does this make to the results of the test done in part (b)? Show all steps for the hypothesis testarrow_forwardQuestion 3 3200 students were asked about the importance of study groups in successfully completing their courses. They were asked to provide their current majors as well as their opinion. The results are given below: Major Opinion Psychology Sociology Economics Statistics Accounting Total Agree 144 183 201 271 251 1050 Disagree 230 233 254 227 218 1162 Impartial 201 181 196 234 176 988 Total 575 597 651 732 645 3200 a. State both the null and alternative hypotheses. b. Provide the decision rule for making this decision. Use an alpha level of 5%. c. Show all of the work necessary to calculate the appropriate statistic. | d. What conclusion are you allowed to draw? c. Would your conclusion change at the 10% level of significance? f. Confirm test results in part (c) using JASP. Note: All JASP input files and output tables should be providedarrow_forwardQuestion 1 A tech company has acknowledged the importance of having records of all meetings conducted. The meetings are very fast paced and requires equipment that is able to capture the information in the shortest possible time. There are two options, using a typewriter or a word processor. Fifteen administrative assistants are selected and the amount of typing time in hours was recorded. The results are given below: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 typewriter 8.0 6.5 5.0 6.7 7.8 8.5 7.2 5.7 9.2 5.7 6.5 word processor 7.2 5.7 8.3 7.5 9.2 7.2 6.5 7.0 6.9 34 7.0 6.9 8.8 6.7 8.8 9.4 8.6 5.5 7.2 8.4 a. Test the hypothesis that the mean typing time in hours for typewriters is less than 7.0. Use the 1% level of significance. b. Construct a 90% confidence interval for the difference in mean typing time in hours, where a difference is equal to the typing time in hours of word processors minus typing time in hours of typewriter. c. Using the 5% significance level, determine whether there is…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning 
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning


Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY