Calculus: Early Transcendentals and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition) (Briggs, Cochran, Gillett & Schulz, Calculus Series)
3rd Edition
ISBN: 9780134995991
Author: William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6.2, Problem 74E
Geometric probability Suppose a dartboard occupies the square {(x, y):0 ≤ |x| ≤ 1, 0 ≤ |y| ≤ 1}. A dart is thrown randomly at the board many times (meaning it is equally likely to land at any point in the square). What fraction of the dart throws land closer to the edge of the board than the center? Equivalently, what is the probability that the dart lands closer to the edge of the board than the center? Proceed as follows.
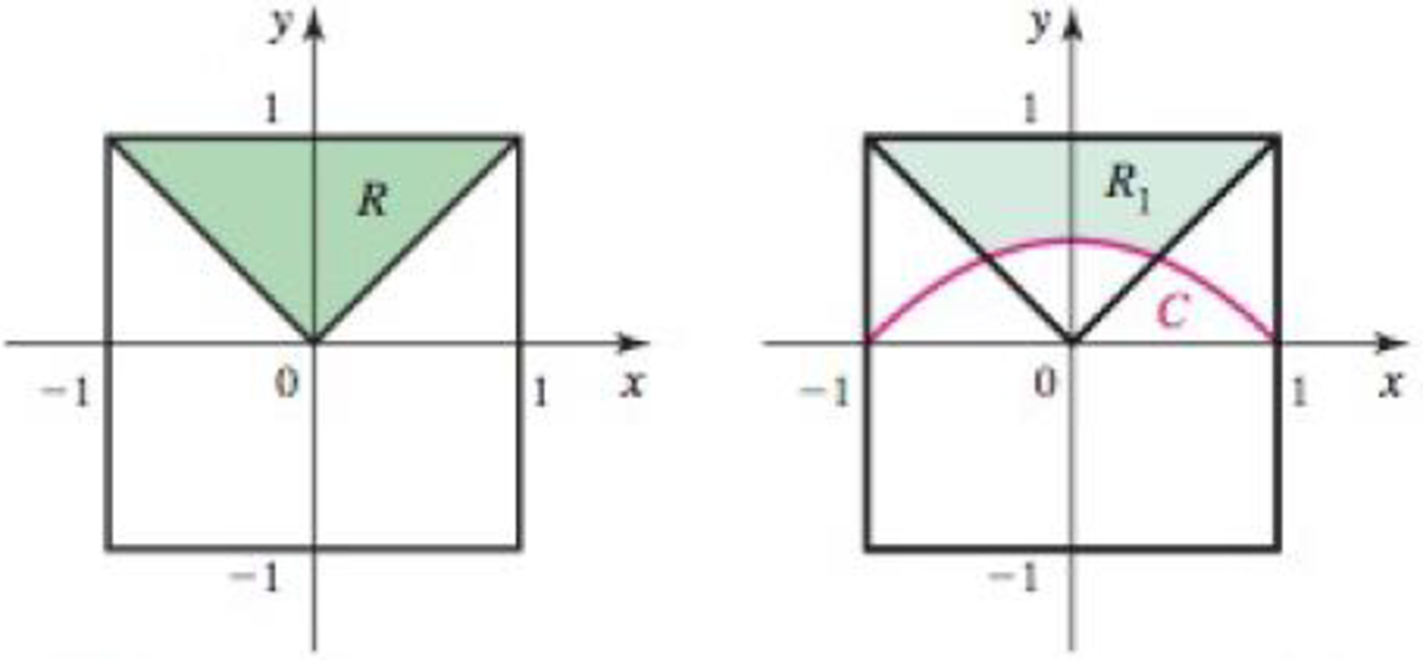
- a. Argue that by symmetry, it is necessary to consider only one quarter of the board, say the region R: {(x, y): |x| ≤ y ≤ 1}.
- b. Find the curve C in this region that is equidistant from the center of the board and the top edge of the board (see figure).
- c. The probability that the dart lands closer to the edge of the board than the center is the ratio of the area of the region R1 above C to the area of the entire region R. Compute this probability.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Ministry of Higher Education &
Scientific Research
Babylon University
College of Engineering -
Al musayab
Automobile Department
Subject :Engineering Analysis
Time: 2 hour
Date:27-11-2022
کورس اول تحليلات
تعمیر )
1st month exam / 1st semester (2022-2023)/11/27
Note: Answer all questions,all questions have same degree.
Q1/: Find the following for three only.
1-
4s
C-1
(+2-3)2 (219) 3.0 (6+1)) (+3+5)
(82+28-3),2-
,3-
2-1
4-
Q2/:Determine the Laplace transform of the function t sint.
Q3/: Find the Laplace transform of
1,
0≤t<2,
-2t+1,
2≤t<3,
f(t) =
3t,
t-1,
3≤t 5,
t≥ 5
Q4: Find the Fourier series corresponding to the function
0
-5
Ministry of Higher Education &
Scientific Research
Babylon University
College of Engineering -
Al musayab
Subject :Engineering Analysis
Time: 80 min
Date:11-12-2022
Automobile Department
2nd month exam / 1" semester (2022-2023)
Note: Answer all questions,all questions have same degree.
کورس اول
شعر 3
Q1/: Use a Power series to solve the differential equation:
y" - xy = 0
Q2/:Evaluate using Cauchy's residue theorem,
sinnz²+cosz²
dz, where C is z = 3
(z-1)(z-2)
Q3/:Evaluate
dz
(z²+4)2
Where C is the circle /z-i/-2,using Cauchy's residue theorem.
Examiner: Dr. Wisam N. Hassan
Ministry of Higher Education &
Scientific Research
Babylon University
College of Engineering -
Al musayab
Subject :Engineering Analysis
Time: 80 min
Date:11-12-2022
Automobile Department
2nd month exam / 1" semester (2022-2023)
Note: Answer all questions,all questions have same degree.
کورس اول
شعر 3
Q1/: Use a Power series to solve the differential equation:
y" - xy = 0
Q2/:Evaluate using Cauchy's residue theorem,
sinnz²+cosz²
dz, where C is z = 3
(z-1)(z-2)
Q3/:Evaluate
dz
(z²+4)2
Where C is the circle /z-i/-2,using Cauchy's residue theorem.
Examiner: Dr. Wisam N. Hassan
Chapter 6 Solutions
Calculus: Early Transcendentals and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition) (Briggs, Cochran, Gillett & Schulz, Calculus Series)
Ch. 6.1 - A police officer leaves his station on a...Ch. 6.1 - Describe a possible motion of an object along a...Ch. 6.1 - Is the position s(t) a number or a function? For...Ch. 6.1 - Without doing further calculations, what are the...Ch. 6.1 - Suppose (unrealistically) in Example 3 that the...Ch. 6.1 - Is the cost of increasing production from 0000...Ch. 6.1 - Explain the meaning of position, displacement, and...Ch. 6.1 - Suppose the velocity of an object moving along a...Ch. 6.1 - Given the velocity function v of an object moving...Ch. 6.1 - Explain how to use definite integrals to find the...
Ch. 6.1 - Prob. 5ECh. 6.1 - What is the result of integrating a population...Ch. 6.1 - Displacement and distance from velocity Consider...Ch. 6.1 - Displacement and distance from velocity Consider...Ch. 6.1 - Velocity graphs The figures show velocity...Ch. 6.1 - Velocity graphs The figures show velocity...Ch. 6.1 - Distance traveled and displacement Suppose an...Ch. 6.1 - Distance traveled and displacement Suppose an...Ch. 6.1 - Displacement from velocity Consider an object...Ch. 6.1 - Displacement from velocity Consider an object...Ch. 6.1 - Displacement from velocity Consider an object...Ch. 6.1 - Displacement from velocity Assume t is time...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Position from velocity Consider an object moving...Ch. 6.1 - Oscillating motion A mass hanging from a spring is...Ch. 6.1 - Cycling distance A cyclist rides down a long...Ch. 6.1 - Flying into a headwind The velocity (in mi/hr) of...Ch. 6.1 - Day hike The velocity (in mi/hr) of a hiker...Ch. 6.1 - Piecewise velocity The velocity of a (fast)...Ch. 6.1 - Probe speed A data collection probe is dropped...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Position and velocity from acceleration Find the...Ch. 6.1 - Acceleration A drag racer accelerates at a(t) = 88...Ch. 6.1 - Deceleration A car slows down with an acceleration...Ch. 6.1 - Approaching a station At t = 0, a train...Ch. 6.1 - Population growth 40. Starting with an initial...Ch. 6.1 - Population growth 41. When records were first kept...Ch. 6.1 - Population growth 42. The population of a...Ch. 6.1 - Population growth 43. A culture of bacteria in a...Ch. 6.1 - Cancer treatment A cancerous tumor in a mouse is...Ch. 6.1 - Oil production An oil refinery produces oil at a...Ch. 6.1 - Flow rates in the Spokane River The daily...Ch. 6.1 - Depletion of natural resources Suppose that r(t) =...Ch. 6.1 - Filling a tank A 2000-liter cistern is empty when...Ch. 6.1 - Filling a reservoir A reservoir with a capacity of...Ch. 6.1 - Blood flow A typical human heart pumps 70 mL of...Ch. 6.1 - Air flow in the lungs A simple model (with...Ch. 6.1 - Oscillating growth rates Some species have growth...Ch. 6.1 - Power and energy Power and energy are often used...Ch. 6.1 - Carbon uptake An important process in the study of...Ch. 6.1 - Marginal cost Consider the following marginal cost...Ch. 6.1 - Marginal cost Consider the following marginal cost...Ch. 6.1 - Marginal cost Consider the following marginal cost...Ch. 6.1 - Prob. 58ECh. 6.1 - Explain why or why not Determine whether the...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Equivalent constant velocity Consider the...Ch. 6.1 - Where do they meet? Kelly started at noon (t = 0)...Ch. 6.1 - Prob. 65ECh. 6.1 - Two runners At noon (t = 0), Alicia starts running...Ch. 6.1 - Snowplow problem With snow on the ground and...Ch. 6.1 - Variable gravity At Earths surface, the...Ch. 6.1 - Another look at the Fundamental Theorem 69....Ch. 6.1 - Another look at the Fundamental Theorem 70. Use...Ch. 6.1 - Another look at the Fundamental Theorem 71. Use...Ch. 6.1 - Another look at the Fundamental Theorem 72....Ch. 6.2 - In the area formula for a region between two...Ch. 6.2 - Interpret the area formula when it is written in...Ch. 6.2 - The region R is bounded by the curve y=x the line...Ch. 6.2 - An alternative way to determine the area of the...Ch. 6.2 - Set up a sum of two integrals that equals the area...Ch. 6.2 - Set up an integral that equals the area of the...Ch. 6.2 - Make a sketch to show a case in which the area...Ch. 6.2 - Make a sketch to show a case in which the area...Ch. 6.2 - Find the area of the region (see figure) in two...Ch. 6.2 - Find the area of the region (see figure) in two...Ch. 6.2 - Express the area of the shaded region in Exercise...Ch. 6.2 - Express the area of the shaded region in Exercise...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Finding area Determine the area of the shaded...Ch. 6.2 - Two approaches Express the area of the following...Ch. 6.2 - Two approaches Express the area of the following...Ch. 6.2 - Area between velocity curves Two runners, starting...Ch. 6.2 - Calculus and geometry For the given regions R1 and...Ch. 6.2 - Calculus and geometry For the given regions R1 and...Ch. 6.2 - Calculus and geometry For the given regions R1 and...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Any method Use any method (including geometry) to...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 52ECh. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Prob. 60ECh. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Regions between curves Find the area of the region...Ch. 6.2 - Complicated regions Find the area of the regions...Ch. 6.2 - Complicated regions Find the area of the regions...Ch. 6.2 - Explain why or why not Determine whether the...Ch. 6.2 - Differences of even functions Assume f and g are...Ch. 6.2 - Area of a curve defined implicitly Determine the...Ch. 6.2 - Prob. 68ECh. 6.2 - Prob. 69ECh. 6.2 - Prob. 70ECh. 6.2 - Prob. 71ECh. 6.2 - Prob. 72ECh. 6.2 - Bisecting regions For each region R, find the...Ch. 6.2 - Geometric probability Suppose a dartboard occupies...Ch. 6.2 - Lorenz curves and the Gini index A Lorenz curve is...Ch. 6.2 - Equal area properties for parabolas Consider the...Ch. 6.2 - Prob. 77ECh. 6.2 - Shifting sines Consider the functions f(x) = a sin...Ch. 6.3 - Why is the volume as given by the general slicing...Ch. 6.3 - In Example 2 what is the cross-sectional area...Ch. 6.3 - What solid results when the region R is revolved...Ch. 6.3 - Show that when g(x) = 0 in the washer method, the...Ch. 6.3 - Suppose the region in Example 4 is revolved about...Ch. 6.3 - The region in the first quadrant bounded by y = x...Ch. 6.3 - Suppose a cut is made through a solid object...Ch. 6.3 - A solid has a circular base and cross sections...Ch. 6.3 - Consider a solid whose base is the region in the...Ch. 6.3 - Why is the disk method a special case of the...Ch. 6.3 - Let R be the region bounded by the curve y=cosx...Ch. 6.3 - Let R be the region bounded by the curve y = cos1x...Ch. 6.3 - Use the region R that is bounded by the graphs of...Ch. 6.3 - Use the region R that is bounded by the graphs of...Ch. 6.3 - Use the region R that is bounded by the graphs of...Ch. 6.3 - Use the region R that is bounded by the graphs of...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - General slicing method Use the general slicing...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Disk method Let R be the region bounded by the...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Washer method Let R be the region bounded by the...Ch. 6.3 - Disks/washers about the y-axis Let R be the region...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - 17-44. Solids of revolution Let R be the region...Ch. 6.3 - Solids of revolution Let R be the region bounded...Ch. 6.3 - Which is greater? For the following regions R,...Ch. 6.3 - Which is greater? For the following regions R,...Ch. 6.3 - Which is greater? For the following regions R,...Ch. 6.3 - Which is greater? For the following regions R,...Ch. 6.3 - Revolution about other axes Let R be the region...Ch. 6.3 - Revolution about other axes Let R be the region...Ch. 6.3 - Revolution about other axes Let R be the region...Ch. 6.3 - Revolution about other axes Let R be the region...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Revolution about other axes Find the volume of the...Ch. 6.3 - Prob. 60ECh. 6.3 - Explain why or why not Determine whether the...Ch. 6.3 - Prob. 62ECh. 6.3 - Fermats volume calculation (1636) Let R be the...Ch. 6.3 - Solid from a piecewise function Let...Ch. 6.3 - Prob. 65ECh. 6.3 - Prob. 66ECh. 6.3 - Estimating volume Suppose the region bounded by...Ch. 6.3 - Volume of a wooden object A solid wooden object...Ch. 6.3 - Cylinder, cone, hemisphere A right circular...Ch. 6.3 - Water in a bowl A hemispherical bowl of radius 8...Ch. 6.3 - A torus (doughnut) Find the volume of the torus...Ch. 6.3 - Which is greater? Let R be the region bounded by y...Ch. 6.3 - Cavalieri’s principle Cavalieri’s principle states...Ch. 6.3 - Prob. 74ECh. 6.4 - The triangle bounded by the x-axis, the line y =...Ch. 6.4 - Write the volume integral in Example 4b in the...Ch. 6.4 - Suppose the region in Example 5 is revolved about...Ch. 6.4 - Assume f and g are continuous with f(x) g(x) on...Ch. 6.4 - Fill in the blanks: A region R is revolved about...Ch. 6.4 - Fill in the blanks: A region R is revolved about...Ch. 6.4 - Look again at the region R in Figure 6.38 (p 439)....Ch. 6.4 - Let R be the region in the first quadrant bounded...Ch. 6.4 - Let R be the region bounded by the curves...Ch. 6.4 - Let R be the region bounded by the curves...Ch. 6.4 - Let R be the region bounded by the curves...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Shell method Let R be the region bounded by the...Ch. 6.4 - Washers vs. shells Let R be the region bounded by...Ch. 6.4 - Prob. 36ECh. 6.4 - Washers vs. shells Let R be the region bounded by...Ch. 6.4 - Shell and washer methods Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Shell method about other lines Let R be the region...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Different axes of revolution Use either the washer...Ch. 6.4 - Volume of a sphere Let R be the region bounded by...Ch. 6.4 - Comparing American and rugby union footballs An...Ch. 6.4 - A torus (doughnut) A torus is formed when a circle...Ch. 6.4 - Prob. 52ECh. 6.4 - Choose your method Let R be the region bounded by...Ch. 6.4 - Choose your method Let R be the region bounded by...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Prob. 58ECh. 6.4 - Choose your method Let R be the region bounded by...Ch. 6.4 - Choose your method Find the volume of the...Ch. 6.4 - Choose your method Let R be the region bounded by...Ch. 6.4 - The solid formed when the region bounded by y=x,...Ch. 6.4 - Explain why or why not Determine whether the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Shell method Use the shell method to find the...Ch. 6.4 - Prob. 69ECh. 6.4 - A spherical cap by three methods Consider the cap...Ch. 6.4 - Change of variables Suppose f(x) 0 for all x and...Ch. 6.4 - Equal integrals Without evaluating integrals,...Ch. 6.4 - Volumes without calculus Solve the following...Ch. 6.4 - Wedge from a tree Imagine a cylindrical tree of...Ch. 6.4 - Prob. 75ECh. 6.4 - Prob. 76ECh. 6.5 - What does the arc length formula give for the...Ch. 6.5 - What does the arc length formula give for the...Ch. 6.5 - Write the integral for the length of the curve x =...Ch. 6.5 - Explain the steps required to find the length of a...Ch. 6.5 - Explain the steps required to find the length of a...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Setting up arc length integrals Write and...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc lezngth calculations Find the arc length of...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Prob. 15ECh. 6.5 - Arc length calculations Find the arc length of the...Ch. 6.5 - Prob. 17ECh. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length calculations with respect to y Find the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a. Write and simplify the...Ch. 6.5 - Arc length by calculator a.Write and simplify the...Ch. 6.5 - Golden Gate cables The profile of the cables on a...Ch. 6.5 - Gateway Arch The shape of the Gateway Arch in St....Ch. 6.5 - Explain why or why not Determine whether the...Ch. 6.5 - Arc length for a line Consider the segment of the...Ch. 6.5 - Functions from arc length What differentiable...Ch. 6.5 - Function from arc length Find a curve that passes...Ch. 6.5 - Prob. 37ECh. 6.5 - Prob. 38ECh. 6.5 - Lengths of related curves Suppose the graph of f...Ch. 6.5 - Prob. 40ECh. 6.5 - A family of exponential functions a. Show that the...Ch. 6.5 - Bernoullis parabolas Johann Bernoulli (16671748)...Ch. 6.6 - Which is greater the surface area of a cone of...Ch. 6.6 - What is the surface area of the frustum of a cone...Ch. 6.6 - Let f(x) = c, where c 0. What surface is...Ch. 6.6 - What is the area of the curved surface of a right...Ch. 6.6 - A frustum of a cone is generated by revolving the...Ch. 6.6 - Suppose f is positive and differentiable on [a,...Ch. 6.6 - Suppose g is positive and differentiable on [c,...Ch. 6.6 - A surface is generated by revolving the line f(x)...Ch. 6.6 - A surface is generated by revolving the line x =...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Revolving about the y-axis Find the area of the...Ch. 6.6 - Revolving about the y-axis Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Computing surface areas Find the area of the...Ch. 6.6 - Surface area calculations Use the method of your...Ch. 6.6 - Surface area calculations Use the method of your...Ch. 6.6 - Painting surfaces A 1.5-mm layer of paint is...Ch. 6.6 - Painting surfaces A 1.5-mm layer of paint is...Ch. 6.6 - Explain why or why not Determine whether the...Ch. 6.6 - Prob. 24ECh. 6.6 - T 2629. Surface area using technology Consider the...Ch. 6.6 - Surface area using technology Consider the...Ch. 6.6 - Surface area using technology Consider the...Ch. 6.6 - Prob. 28ECh. 6.6 - Prob. 29ECh. 6.6 - Cones and cylinders The volume of a cone of radius...Ch. 6.6 - Challenging surface area calculations Find the...Ch. 6.6 - Challenging surface area calculations Find the...Ch. 6.6 - Challenging surface area calculations Find the...Ch. 6.6 - Challenging surface area calculations Find the...Ch. 6.6 - Surface area calculations Use the method of your...Ch. 6.6 - Surface area of a torus When the circle x2 + (y ...Ch. 6.6 - Zones of a sphere Suppose a sphere of radius r is...Ch. 6.6 - Prob. 38ECh. 6.6 - Surface-area-to-volume ratio (SAV) In the design...Ch. 6.6 - Surface area of a frustum Show that the surface...Ch. 6.6 - Scaling surface area Let f be a nonnegative...Ch. 6.6 - Surface plus cylinder Suppose f is a nonnegative...Ch. 6.7 - In Figure 6.69, suppose a = 0, b = 3, and the...Ch. 6.7 - A thin bar occupies the interval 0 x 2 and has a...Ch. 6.7 - Prob. 3QCCh. 6.7 - Prob. 4QCCh. 6.7 - In Example 3b, the bucket occupies the interval...Ch. 6.7 - Prob. 6QCCh. 6.7 - In Example 4, how would the integral change if the...Ch. 6.7 - Suppose a 1-m cylindrical bar has a constant...Ch. 6.7 - Explain how to find the mass of a one-dimensional...Ch. 6.7 - How much work is required to move an object from x...Ch. 6.7 - Why is integration used to find the work done by a...Ch. 6.7 - Why is integration used to find the work required...Ch. 6.7 - Why is integration used to find the total force on...Ch. 6.7 - What is the pressure on a horizontal surface with...Ch. 6.7 - Explain why you integrate in the vertical...Ch. 6.7 - Consider the cylindrical tank in Example 4 that...Ch. 6.7 - Consider the cylindrical tank in Example 4 that...Ch. 6.7 - Consider the cylindrical tank in Example 4 that...Ch. 6.7 - Consider the cylindrical tank in Example 4 that...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Mass of one-dimensional objects Find the mass of...Ch. 6.7 - Work from force How much work is required to move...Ch. 6.7 - Work from force How much work is required to move...Ch. 6.7 - Compressing and stretching a spring Suppose a...Ch. 6.7 - Compressing and stretching a spring Suppose a...Ch. 6.7 - Work done by a spring A spring on a horizontal...Ch. 6.7 - Shock absorber A heavy-duty shock absorber is...Ch. 6.7 - Calculating work for different springs Calculate...Ch. 6.7 - Calculating work for different springs Calculate...Ch. 6.7 - Calculating work for different springs Calculate...Ch. 6.7 - Work function A spring has a restoring force given...Ch. 6.7 - Winding a chain A 30-m-long chain hangs vertically...Ch. 6.7 - Coiling a rope A 60-m-long, 9.4-mm-diameter rope...Ch. 6.7 - Winding part of a chain A 20-m-long, 50-kg chain...Ch. 6.7 - Leaky Bucket A 1-kg bucket resting on the ground...Ch. 6.7 - Emptying a swimming pool A swimming pool has the...Ch. 6.7 - Emptying a cylindrical tank A cylindrical water...Ch. 6.7 - Emptying a half-full cylindrical tank Suppose the...Ch. 6.7 - Emptying a partially filled swimming pool If the...Ch. 6.7 - Emptying a conical tank A water tank is shaped...Ch. 6.7 - Upper and lower half A cylinder with height 8 m...Ch. 6.7 - Filling a spherical tank A spherical water tank...Ch. 6.7 - Emptying a water trough A water trough has a...Ch. 6.7 - Emptying a water trough A cattle trough has a...Ch. 6.7 - Pumping water Suppose the tank in Example 5 is...Ch. 6.7 - Emptying a conical tank An inverted cone is 2 m...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Force on dams The following figures show the shape...Ch. 6.7 - Parabolic dam The lower edge of a dam is defined...Ch. 6.7 - Prob. 51ECh. 6.7 - Force on a window A diving pool that is 4 m deep...Ch. 6.7 - Force on a window A diving pool that is 4 m deep...Ch. 6.7 - Force on a window A diving pool that is 4 m deep...Ch. 6.7 - Force on a building A large building shaped like a...Ch. 6.7 - Force on the end of a tank Determine the force on...Ch. 6.7 - Explain why or why not Determine whether the...Ch. 6.7 - Prob. 58ECh. 6.7 - A nonlinear spring Hookes law is applicable to...Ch. 6.7 - Prob. 60ECh. 6.7 - Leaky cement bucket A 350 kg-bucket containing...Ch. 6.7 - Emptying a real swimming pool A swimming pool is...Ch. 6.7 - Drinking juice A glass has circular cross sections...Ch. 6.7 - Lifting a pendulum A body of mass m is suspended...Ch. 6.7 - Critical depth A large tank has a plastic window...Ch. 6.7 - Prob. 66ECh. 6.7 - Prob. 67ECh. 6.7 - Prob. 68ECh. 6.7 - Work in a gravitational field For large distances...Ch. 6.7 - Buoyancy Archimedes principle says that the...Ch. 6 - Explain why or why not Determine whether the...Ch. 6 - Prob. 2RECh. 6 - Displacement, distance, and position Consider an...Ch. 6 - Displacement from velocity The velocity of an...Ch. 6 - Position, displacement, and distance A projectile...Ch. 6 - Deceleration At t = 0, a car begins decelerating...Ch. 6 - An oscillator The acceleration of an object moving...Ch. 6 - A race Starting at the same point on a straight...Ch. 6 - Fuel consumption A small plane in flight consumes...Ch. 6 - Variable flow rate Water flows out of a tank at a...Ch. 6 - Decreasing velocity A projectile is fired upward,...Ch. 6 - Decreasing velocity A projectile is fired upward,...Ch. 6 - An exponential bike ride Tom and Sue took a bike...Ch. 6 - Areas of regions Determine the area of the given...Ch. 6 - Areas of regions Determine the area of the given...Ch. 6 - Areas of regions Determine the area of the given...Ch. 6 - Areas of regions Determine the area of the given...Ch. 6 - Prob. 18RECh. 6 - Areas of regions Use any method to find the area...Ch. 6 - Areas of regions Determine the area of the given...Ch. 6 - Areas of regions Use any method to find the area...Ch. 6 - Areas of regions Use any method to find the area...Ch. 6 - Areas of regions Use any method to find the area...Ch. 6 - Prob. 24RECh. 6 - Areas of regions Determine the area of the given...Ch. 6 - Multiple regions Determine the area of the region...Ch. 6 - Multiple regions The regions R1, R2, and R3 (see...Ch. 6 - Prob. 28RECh. 6 - Multiple regions The regions R1, R2, and R3 (see...Ch. 6 - Prob. 30RECh. 6 - Multiple regions The regions R1, R2, and R3 (see...Ch. 6 - Multiple regions The regions R1, R2, and R3 (see...Ch. 6 - Multiple regions The regions R1, R2, and R3 (see...Ch. 6 - Area and volume The region R is bounded by the...Ch. 6 - Area and volume Let R be the region in the first...Ch. 6 - Area and volume Let R be the region in the first...Ch. 6 - Area and volume Let R be the region in the first...Ch. 6 - Area and volume Let R be the region in the first...Ch. 6 - Find the area of the shaded regions R1 and R2...Ch. 6 - Prob. 40RECh. 6 - Prob. 41RECh. 6 - Two methods The region R in the first quadrant...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Volumes of solids Choose the general slicing...Ch. 6 - Comparing volumes Let R be the region bounded by y...Ch. 6 - Comparing volumes Let R be the region bounced by...Ch. 6 - Arc length Find the length of the following...Ch. 6 - Arc length Find the length of the following...Ch. 6 - Arc length Find the length of the following...Ch. 6 - Arc length Find the length of the following...Ch. 6 - Arc length by calculator Write and simplify the...Ch. 6 - Arc length by calculator Write and simplify the...Ch. 6 - Arc length by calculator Write and simplify the...Ch. 6 - Arc length by calculator Write and simplify the...Ch. 6 - Surface area and volume Let f(x)=13x3 and let R be...Ch. 6 - Surface area and volume Let f(x)=3xx2 and let R be...Ch. 6 - Surface area of a cone Find the surface area of a...Ch. 6 - Surface area and more Let f(x)=x42+116x2 and let R...Ch. 6 - Variable density in one dimension Find the mass of...Ch. 6 - Variable density in one dimension Find the mass of...Ch. 6 - Variable density in one dimension Find the mass of...Ch. 6 - Spring work a. It lakes 50 J of work to stretch a...Ch. 6 - Leaky bucket A 1-kg bucket resting on the ground...Ch. 6 - Lifting problem A 10-m, 20-kg chain hangs...Ch. 6 - Lifting problem A 4-kg mass is attached to the...Ch. 6 - Pumping water A water tank has the shape of a box...Ch. 6 - Pumping water A cylindrical water tank has a...Ch. 6 - Pumping water A water tank that is full of water...Ch. 6 - Pumping water A water tank that has the shape of a...Ch. 6 - Pumping water A tank has the shape of the surface...Ch. 6 - Fluid Forces Suppose the Mowing plates are placed...Ch. 6 - Fluid Forces Suppose the Mowing plates are placed...Ch. 6 - Fluid Forces Suppose the Mowing plates are placed...Ch. 6 - Force on a dam Find the total force on the face of...Ch. 6 - Equal area property for parabolas Let f(x) = ax2 +...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Why dividing could be factoring.
Pre-Algebra Student Edition
CHECK POINT I You deposit $3000 in s savings account at Yourtown Bank, which has rate of 5%. Find the interest ...
Thinking Mathematically (6th Edition)
Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...
College Algebra with Modeling & Visualization (5th Edition)
Coke versus Pepsi (Example 5) Suppose you are testing someone to see whether she or he can tell Coke from Pepsi...
Introductory Statistics
Constructing and Interpreting Confidence Intervals. In Exercises 13–16, use the given sample data and confidenc...
Elementary Statistics (13th Edition)
For what values of a is
continuous at every x?
University Calculus: Early Transcendentals (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Which degenerate conic is formed when a double cone is sliced through the apex by a plane parallel to the slant edge of the cone?arrow_forward1/ Solve the following: 1 x + X + cos(3X) -75 -1 2 2 (5+1) e 5² + 5 + 1 3 L -1 1 5² (5²+1) 1 5(5-5)arrow_forwardI need expert handwritten solution.to this integralarrow_forward
- Example: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardExample: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardPlease can you give detailed steps on how the solutions change from complex form to real form. Thanks.arrow_forward
- Examples: Solve the following differential equation using Laplace transform (e) ty"-ty+y=0 with y(0) = 0, and y'(0) = 1arrow_forwardExamples: Solve the following differential equation using Laplace transform (a) y" +2y+y=t with y(0) = 0, and y'(0) = 1arrow_forwardπ 25. If lies in the interval <0arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Propositional Logic, Propositional Variables & Compound Propositions; Author: Neso Academy;https://www.youtube.com/watch?v=Ib5njCwNMdk;License: Standard YouTube License, CC-BY
Propositional Logic - Discrete math; Author: Charles Edeki - Math Computer Science Programming;https://www.youtube.com/watch?v=rL_8y2v1Guw;License: Standard YouTube License, CC-BY
DM-12-Propositional Logic-Basics; Author: GATEBOOK VIDEO LECTURES;https://www.youtube.com/watch?v=pzUBrJLIESU;License: Standard Youtube License
Lecture 1 - Propositional Logic; Author: nptelhrd;https://www.youtube.com/watch?v=xlUFkMKSB3Y;License: Standard YouTube License, CC-BY
MFCS unit-1 || Part:1 || JNTU || Well formed formula || propositional calculus || truth tables; Author: Learn with Smily;https://www.youtube.com/watch?v=XV15Q4mCcHc;License: Standard YouTube License, CC-BY