Chapter 6.1, Problem 2PSA

a.

To determine

To find value of intersection of r plane and s plane.

Answer to Problem 2PSA

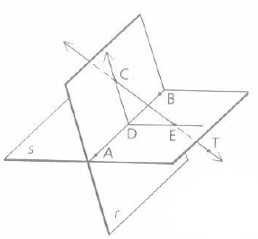
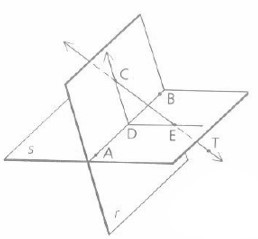
The value of intersection of r plane and s plane is line AB.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

  $r\cap s$

Calculation:

  

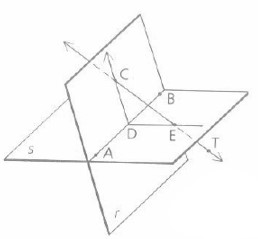
Two planes always intersect in a line as long as they are not parallel.

The r and s plane share a common line AB.

b.

To determine

To find value of intersection of line AB and s plane.

Answer to Problem 2PSA

The value of intersection of line AB and s plane is line AB.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

  $\overline{AB}\cap s$

Calculation:

  

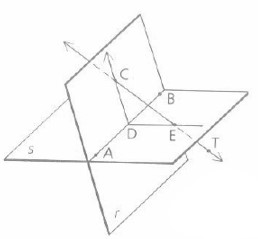
Two planes always intersect in a line as long as they are not parallel.

The r and s plane share a common line AB.

c.

To determine

To find the three collinear points.

Answer to Problem 2PSA

The three collinear points are $C,E,TorA,D,B$ .

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

Calculation:

  

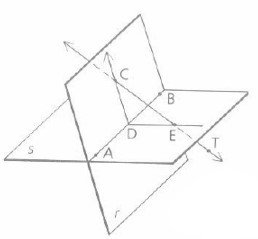
Collinear points are points which lie on same line.

  $C,E,TorA,D,B$ are points which lie on same line.

d.

To determine

To find four non coplanar points.

Answer to Problem 2PSA

The four non coplanar points are $A,C,E,T$ .

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

Calculation:

  

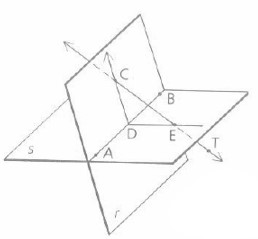
A group of points that do not lie on the same plane are non-coplanar.

Point A lie on $\overline{AB},$ point E lie in s plane, point C lies on r plane and point T on $\overline{CT}$ .

e.

To determine

To find the plane formed by the points A, B and E.

Answer to Problem 2PSA

The plane formed by the points A, B and E is s plane.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

Calculation:

  

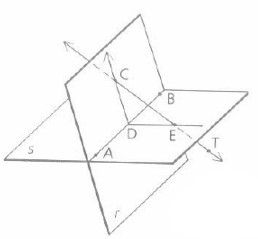
A group of points that lie in the same plane are coplanar.

Points A and B lie on line AB and point E lie on line CT. They altogether lie in s plane

f.

To determine

To find the plane formed by lines AB and ED.

Answer to Problem 2PSA

The plane formed by lines AB and ED is s plane.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

Calculation:

  

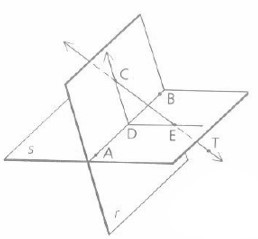
A number of lines that lie in the same plane are coplanar.

Line AB is common to both s plane and r plane. Line ED lie in s plane. They altogether lie in s plane.

g.

To determine

To find the foot of a line TC in s plane.

Answer to Problem 2PSA

The foot of a line TC in s plane is point E.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

Calculation:

  

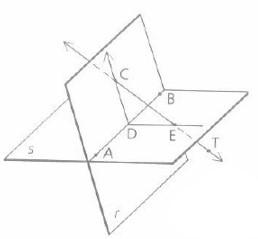
A line that intersects at a point of a plane is called foot.

  $\overleftrightarrow{TC}$ intersects s plane at point E.

h.

To determine

To find the foot of a line TC in r plane.

Answer to Problem 2PSA

The foot of a line TC in r plane is point C.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

Calculation:

  

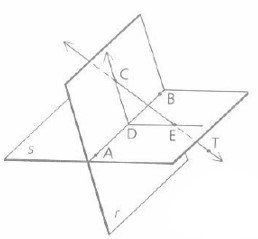
A line that intersects at a point of a plane is called foot.

  $\overleftrightarrow{TC}$ intersects r plane at point C.

i.

To determine

To show whether lines CD and ED represent a plane.

Answer to Problem 2PSA

Yes, lines CD and ED represent a plane.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

Proof:

  

A plane is a flat, two dimensional surface that extends infinitely far.

  $\overleftrightarrow{CD}$ lie in r plane and $\overleftrightarrow{ED}$ lie in s plane. This two lines represent a plane.

j.

To determine

To find the right angles formed if CD is perpendicular to AB.

Answer to Problem 2PSA

  $\angle CDBand\angle CDA$ are the right angles formed if CD is perpendicular to AB.

Explanation of Solution

Given:

The r and s plane intersect at line AB.

  $\overline{CT}$ intersects r and s plane.

  $\overleftrightarrow{CD}\perp \overleftrightarrow{AB}$

Calculation:

  

If a line is perpendicular to another line, it forms two right angles.

  $\overleftrightarrow{CD}\perp \overleftrightarrow{AB}$

  $\angle CDB$ and $\angle CDA$ are right angles formed.