Chapter 6, Problem 85CP

A square-wave generator produces the voltage waveform shown in Fig. 6.94(a). What kind of a circuit component is needed to convert the voltage waveform to the triangular current waveform shown in Fig. 6.94(b)? Calculate the value of the component, assuming that it is initially uncharged.

Figure 6.94

For Prob. 6.85.

To determine

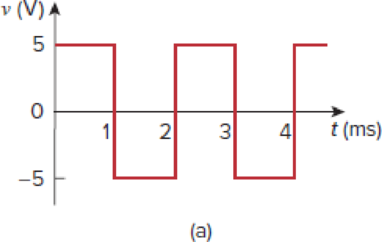
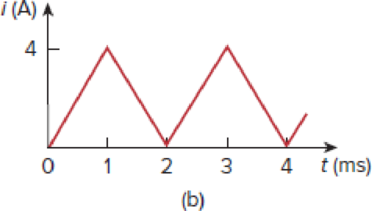
Find the circuit component that is needed to convert the voltage waveform into the triangular current waveform and to calculate the value of the circuit component.

Answer to Problem 85CP

The circuit component inductor is needed to convert the given voltage waveform into the triangular current waveform and the value for the inductor $\left(L\right)$ is $1.25\text{mH}$.

Explanation of Solution

Given data:

Refer to Figure 6.94 in the textbook.

Formula used:

Write the expression to calculate the straight line equation for two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$.

$\left(y-y_1\right)=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)$ (1)

Refer to Figure 6.94(b) in the textbook.

From the given graph, substitute $t$ for $x$ and $i$ for $y$ in equation (1).

$\left(i-y_1\right)=\frac{y_2-y_1}{x_2-x_1}\left(t-x_1\right)$ (2)

Calculation:

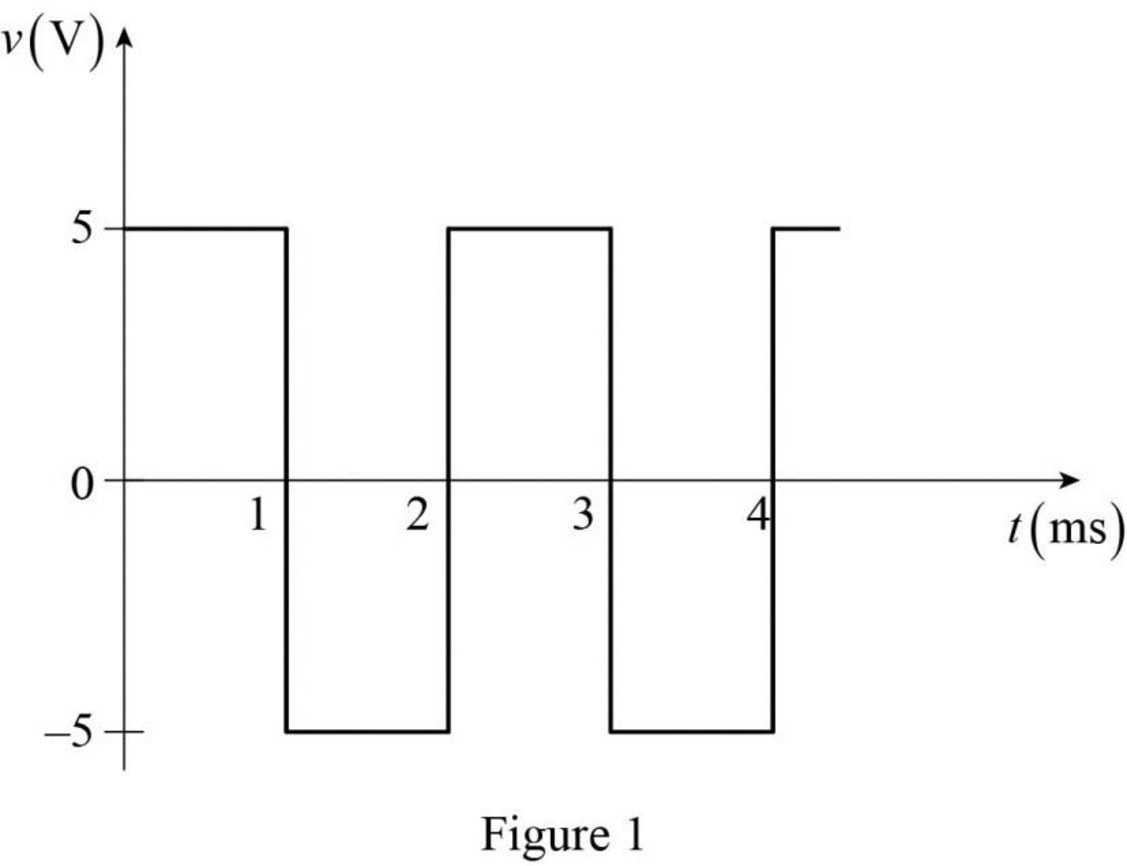
The given voltage waveform is redrawn as Figure 1.

The given triangular current waveform is redrawn as Figure 2.

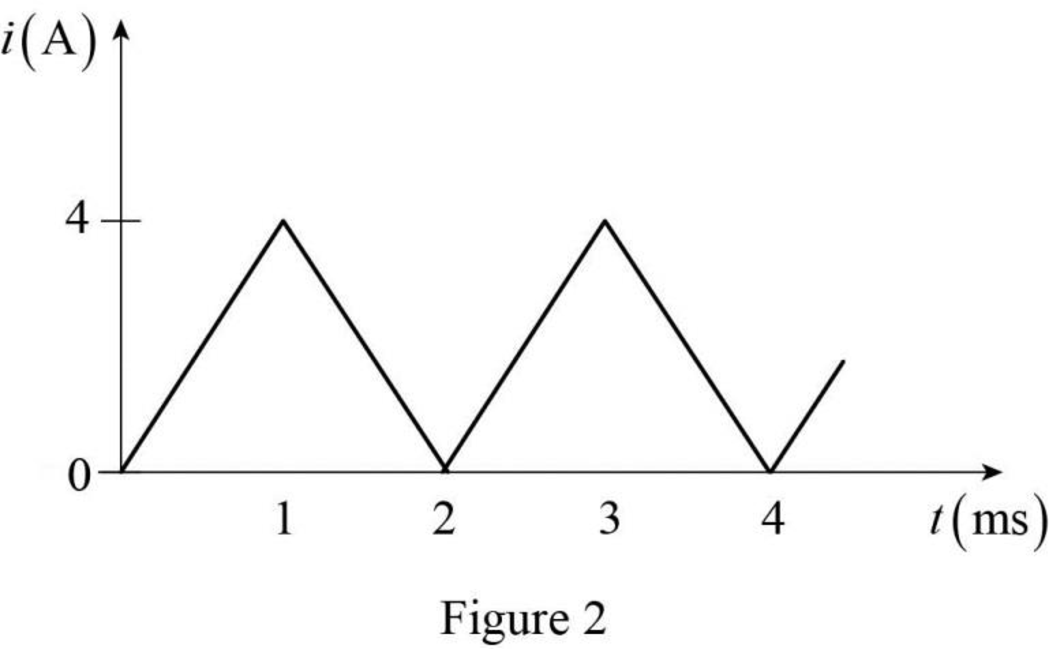
Refer to Figure 1 and Figure 2. Generally, integration of the square waveform gives the triangular waveform. That is, the integration of the voltage waveform gives the current waveform. Such relation can be obtained in following relation.

$i=\frac{1}{L}{\displaystyle \int vdt}$ (3)

Here,

$i$ is the current through the inductor,

$L$ is the value of the inductor, and

$v$ is the voltage across the inductor.

Refer to equation (3), the circuit component inductor is needed to convert the square voltage waveform to the triangular current waveform.

Differentiate the equation (3) with respect to $t$ to find $\frac{di}{dt}$.

$\begin{array}{c}\frac{di}{dt}=\frac{d}{dt}\left(\frac{1}{L}{\displaystyle \int vdt}\right)\\ =\frac{1}{L}\left(\frac{d}{dt}{\displaystyle \int vdt}\right)\\ =\frac{v}{L}\end{array}$

Rearrange the above equation to find $v$.

$v=L\frac{di}{dt}$ (4)

Refer to Figure 1. The voltage function is expressed as,

$v=\{\begin{array}{l}5\text{V},0\text{ms}<t<1\text{ms}\\ -5\text{V},1\text{ms}<t<2\text{ms}\\ 5\text{V,}2\text{ms}<t<3\text{ms}\\ -5\text{V,}3\text{ms}<t<4\text{ms}\end{array}$ (5)

Refer to Figure 2, split up the time period as four divisions $0\text{ms}<t<1\text{ms}$, $1\text{ms}<t<2\text{ms}$, $2\text{ms}<t<3\text{ms}$ and $3\text{ms}<t<4\text{ms}$ to find the respective current value.

Case (i): $0\text{ms}<t<1\text{ms}$

The two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ are $\left(0\text{ms},\text{0}\text{A}\right)$ and $\left(1\text{ms},\text{4}\text{A}\right)$.

Substitute $0\text{ms}$ for $x_1$, $\text{0}\text{A}$ for $y_1$, $1\text{ms}$ for $x_2$ and $4\text{A}$ for $y_2$ in equation (2).

$\begin{array}{c}\left(i-\text{0}\text{A}\right)=\frac{4\text{A}-\text{0}\text{A}}{1\text{ms}-0\text{ms}}\left(t-0\text{ms}\right)\\ =\frac{4\text{A}}{1\text{ms}}t\\ =\frac{4\text{A}}{1\times {10}^{-3}}t\left\{\because 1\text{m}={10}^{-3}\right\}\\ =4000t\text{A}\end{array}$

Simplify the equation to find $i$.

$\begin{array}{c}i=4000t\text{A}+0\text{A}\\ =4000t\text{A}\end{array}$

Case (ii): $1\text{ms}<t<2\text{ms}$

The two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ are $\left(1\text{ms},\text{4}\text{A}\right)$ and $\left(2\text{ms},\text{0}\text{A}\right)$.

Substitute $1\text{ms}$ for $x_1$, $\text{4}\text{A}$ for $y_1$, $2\text{ms}$ for $x_2$ and $0\text{A}$ for $y_2$ in equation (2).

$\begin{array}{c}\left(i-\text{4}\text{A}\right)=\frac{0\text{A}-\text{4}\text{A}}{2\text{ms}-1\text{ms}}\left(t-1\text{ms}\right)\\ =\frac{-\text{4}\text{A}}{1\text{ms}}\left(t-1\text{ms}\right)\\ =\frac{-4\text{A}}{1\times {10}^{-3}}\left(t-\left(1\times {10}^{-3}\right)\right)\left\{\because 1\text{m}={10}^{-3}\right\}\\ =-4000\left(t-0.001\right)\text{A}\end{array}$

Simplify the equation to find $i$.

$\begin{array}{c}i=-4000t\text{A}+4\text{A}+4\text{A}\\ =-4000t\text{A}+8\text{A}\\ =\left(8-4000t\right)\text{A}\end{array}$

Case (iii): $2\text{ms}<t<3\text{ms}$

The two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ are $\left(2\text{ms},\text{0}\text{A}\right)$ and $\left(3\text{ms},\text{4}\text{A}\right)$.

Substitute $2\text{ms}$ for $x_1$, $\text{0}\text{A}$ for $y_1$, $3\text{ms}$ for $x_2$ and $4\text{A}$ for $y_2$ in equation (2).

$\begin{array}{c}\left(i-\text{0}\text{A}\right)=\frac{4\text{A}-\text{0}\text{A}}{3\text{ms}-2\text{ms}}\left(t-2\text{ms}\right)\\ =\frac{4\text{A}}{1\text{ms}}\left(t-2\text{ms}\right)\\ =\frac{4\text{A}}{1\times {10}^{-3}}\left(t-\left(2\times {10}^{-3}\right)\right)\left\{\because 1\text{m}={10}^{-3}\right\}\\ =4000\left(t-0.002\right)\text{A}\end{array}$

Simplify the equation to find $i$.

$\begin{array}{c}i=4000t\text{A}-8\text{A}+0\text{A}\\ =4000t\text{A}-8\text{A}\\ =\left(4000t-8\right)\text{A}\end{array}$

Case (iv): $3\text{ms}<t<4\text{ms}$

The two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ are $\left(3\text{ms},\text{4}\text{A}\right)$ and $\left(4\text{ms},\text{0}\text{A}\right)$.

Substitute $3\text{ms}$ for $x_1$, $\text{4}\text{A}$ for $y_1$, $4\text{ms}$ for $x_2$ and $0\text{A}$ for $y_2$ in equation (2).

$\begin{array}{c}\left(i-\text{4}\text{A}\right)=\frac{0\text{A}-\text{4}\text{A}}{4\text{ms}-3\text{ms}}\left(t-3\text{ms}\right)\\ =-\frac{4\text{A}}{1\text{ms}}\left(t-3\text{ms}\right)\\ =-\frac{4\text{A}}{1\times {10}^{-3}}\left(t-\left(3\times {10}^{-3}\right)\right)\left\{\because 1\text{m}={10}^{-3}\right\}\\ =-4000\left(t-0.003\right)\text{A}\end{array}$

Simplify the equation to find $i$.

$\begin{array}{c}i=-4000t\text{A}+12\text{A}+4\text{A}\\ =-4000t\text{A}+16\text{A}\\ =\left(16-4000t\right)\text{A}\end{array}$

Therefore, the current function of the signal in Figure 2 is,

$i=\{\begin{array}{l}4000t\text{A},0\text{ms}<t<1\text{ms}\\ \left(8-4000t\right)\text{A},1\text{ms}<t<2\text{ms}\\ \left(4000t-8\right)\text{A,}2\text{ms}<t<3\text{ms}\\ \left(16-4000t\right)\text{A,}3\text{ms}<t<4\text{ms}\end{array}$

For $0\text{ms}<t<1\text{ms}$:

Substitute $4000t\text{A}$ for $i$ in equation (4) to find $v$.

$\begin{array}{c}v=L\frac{d\left(4000t\text{A}\right)}{dt}\\ =L\left(4000\right)\frac{d}{dt}\left(t\right)\text{A}\\ =4000L\left(1\right)\frac{\text{A}}{\text{s}}\\ =4000L\frac{\text{A}}{\text{s}}\end{array}$

For $1\text{ms}<t<2\text{ms}$:

Substitute $\left(8-4000t\right)\text{A}$ for $i$ in equation (4) to find $v$.

$\begin{array}{c}v=L\frac{d\left(\left(8-4000t\right)\text{A}\right)}{dt}\\ =L\frac{d}{dt}\left(8-4000t\right)\text{A}\\ =L\left(0-4000\left(1\right)\right)\frac{\text{A}}{\text{s}}\\ =-4000L\frac{\text{A}}{\text{s}}\end{array}$

For $2\text{ms}<t<3\text{ms}$:

Substitute $\left(4000t-8\right)\text{A}$ for $i$ in equation (4) to find $v$.

$\begin{array}{c}v=L\frac{d\left(\left(4000t-8\right)\text{A}\right)}{dt}\\ =L\frac{d}{dt}\left(4000t-8\right)\text{A}\\ =L\left(4000\left(1\right)-0\right)\frac{\text{A}}{\text{s}}\\ =4000L\frac{\text{A}}{\text{s}}\end{array}$

For $3\text{ms}<t<4\text{ms}$:

Substitute $\left(16-4000t\right)\text{A}$ for $i$ in equation (4) to find $v$.

$\begin{array}{c}v=L\frac{d\left(\left(16-4000t\right)\text{A}\right)}{dt}\\ =L\frac{d}{dt}\left(16-4000t\right)\text{A}\\ =L\left(0-4000\left(1\right)\right)\frac{\text{A}}{\text{s}}\\ =-4000L\frac{\text{A}}{\text{s}}\end{array}$

Therefore, the voltage function of the Figure 2 is expressed as,

$v=\{\begin{array}{l}4000L\frac{\text{A}}{\text{s}},0\text{ms}<t<1\text{ms}\\ -4000L\frac{\text{A}}{\text{s}},1\text{ms}<t<2\text{ms}\\ 4000L\frac{\text{A}}{\text{s}}\text{,}2\text{ms}<t<3\text{ms}\\ -4000L\frac{\text{A}}{\text{s}}\text{,}3\text{ms}<t<4\text{ms}\end{array}$ (6)

The voltage function of the signal in Figure 1 is equal to the voltage function that is obtained in equation (6).

Compare the equations (5) and (6) for any of the time limits. Assume the comparison is made for $0\text{ms}<t<1\text{ms}$.

$4000L\frac{\text{A}}{\text{s}}=5\text{V}$

Rearrange the above equation to find $L$.

$\begin{array}{c}\text{L}=\left(\frac{5}{4000}\right)\frac{\text{V}\cdot \text{s}}{\text{A}}\\ =0.00125\text{H}\left\{\because 1\text{H}=\frac{\text{1V}\cdot 1\text{s}}{\text{1A}}\right\}\\ =0.00125\times {10}^3\times {10}^{-3}\text{H}\\ =1.25\text{mH}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Therefore, the circuit component inductor is needed to convert the given voltage waveform into the triangular current waveform and the value for the inductor $\left(L\right)$ is $1.25\text{mH}$.

Conclusion:

Thus, the circuit component inductor is needed to convert the given voltage waveform into the triangular current waveform and the value for the inductor $\left(L\right)$ is $1.25\text{mH}$.