Chapter 6, Problem 23P

Using Fig. 6.57, design a problem that will help other students better understand how capacitors work together when connected in series and in parallel.

Figure 6.57

To determine

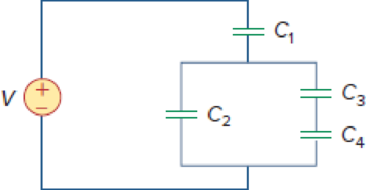
Design a problem to make better understand how capacitors work together when connected in series and in parallel using Figure 6.57.

Explanation of Solution

Problem design:

For the circuit in Figure 6.57, determine the voltage across each capacitor and the energy stored in each capacitor.

Formula used:

Write the expression to calculate the energy stored in the capacitor.

$w=\frac{1}{2}C{V}^2$        (1)

Here,

$C$ is the value of the capacitor, and

$V$ is the voltage across the capacitor.

Calculation:

Refer to Figure 6.57 in the textbook. The Figure 6.57 is redrawn as Figure 1 by assuming the voltage and capacitor values.

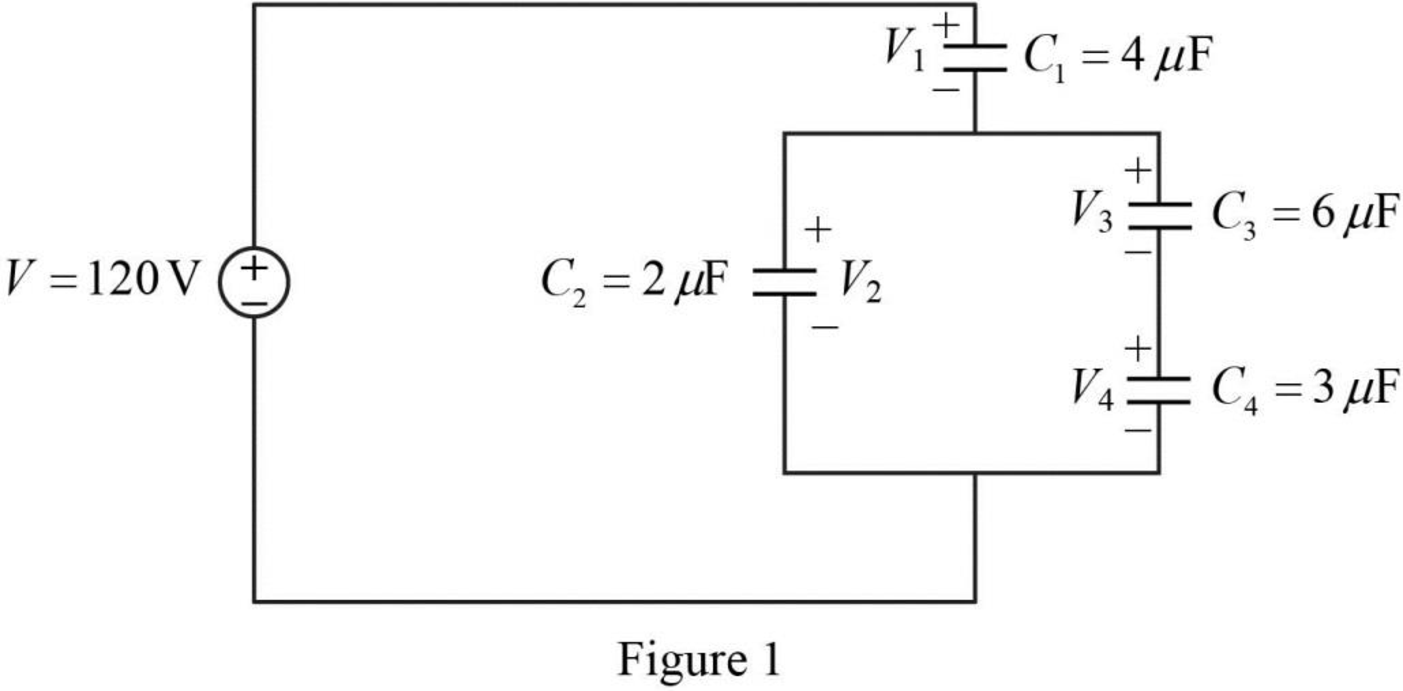
Refer to Figure 1, the capacitors $C_3$ and $C_4$ are connected in series form.

Write the expression to calculate the equivalent capacitance 1 for the series connected capacitors $C_3$ and $C_4$.

$C_{\text{eq1}}=\frac{C_3{C}_4}{C_3+C_4}$        (2)

Here,

$C_3$ is the value of the capacitor 3, and

$C_4$ is the value of the capacitor 4.

Substitute $6\mu \text{F}$ for $C_3$ and $3\mu \text{F}$ for $C_4$ in equation (2) to find $C_{\text{eq1}}$.

$\begin{array}{c}{C}_{\text{eq1}}=\frac{\left(6\mu \text{F}\right)\left(3\mu \text{F}\right)}{6\mu \text{F}+3\mu \text{F}}\\ =\frac{18{\left(\mu \text{F}\right)}^2}{9\mu \text{F}}\\ =2\mu \text{F}\end{array}$

The reduced circuit of the Figure 1 is drawn as Figure 2.

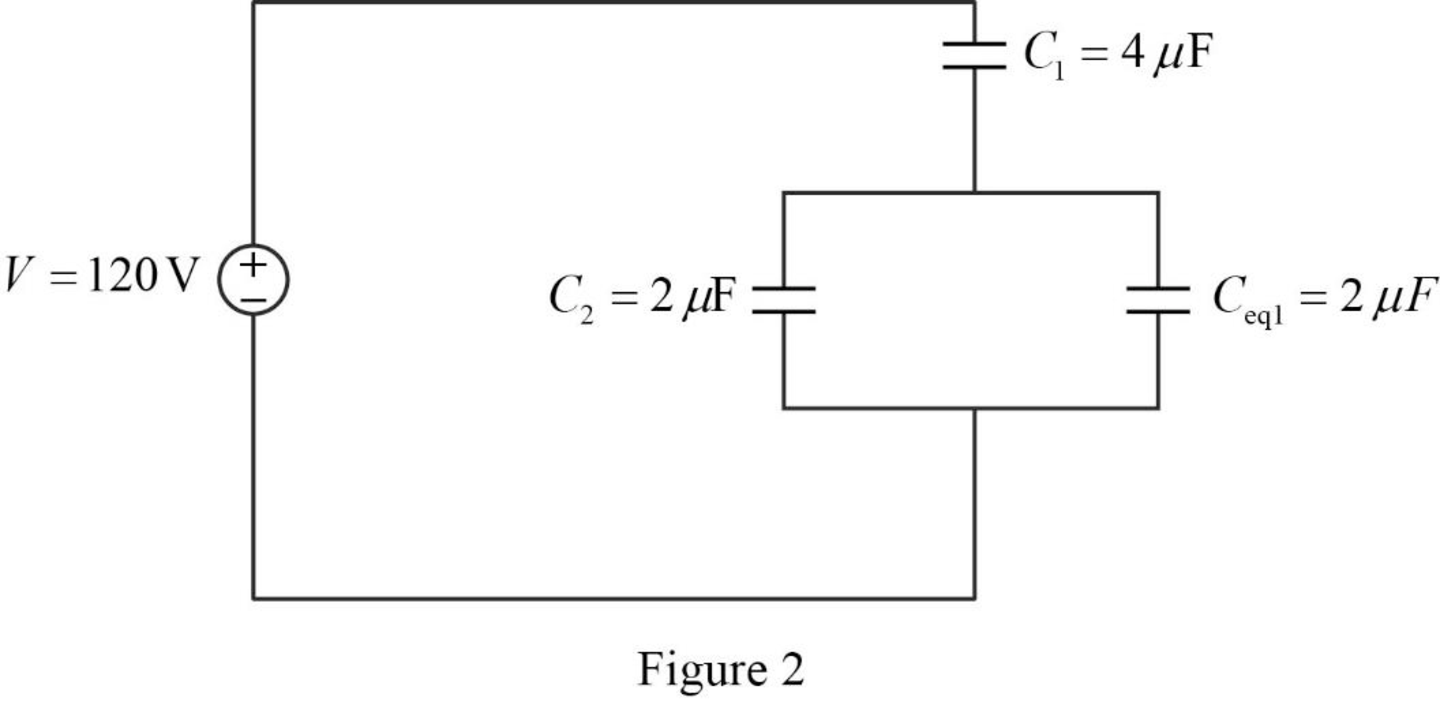
Refer to Figure 2, the capacitors $C_2$ and $C_{\text{eq1}}$ are connected in parallel form.

Write the expression to calculate the equivalent capacitance 2 for the parallel connected capacitors $C_2$ and $C_{\text{eq1}}$.

$C_{\text{eq2}}=C_2+C_{\text{eq1}}$        (3)

Here,

$C_2$ is the value of the capacitor 2, and

$C_{\text{eq1}}$ is the value of the equivalent capacitance 1.

Substitute $2\mu \text{F}$ for $C_2$ and $2\mu \text{F}$ for $C_{\text{eq1}}$ in equation (3) to find $C_{\text{eq2}}$.

$\begin{array}{c}{C}_{\text{eq2}}=2\mu \text{F}+2\mu \text{F}\\ =4\mu \text{F}\end{array}$

The reduced circuit of the Figure 2 is drawn as Figure 3.

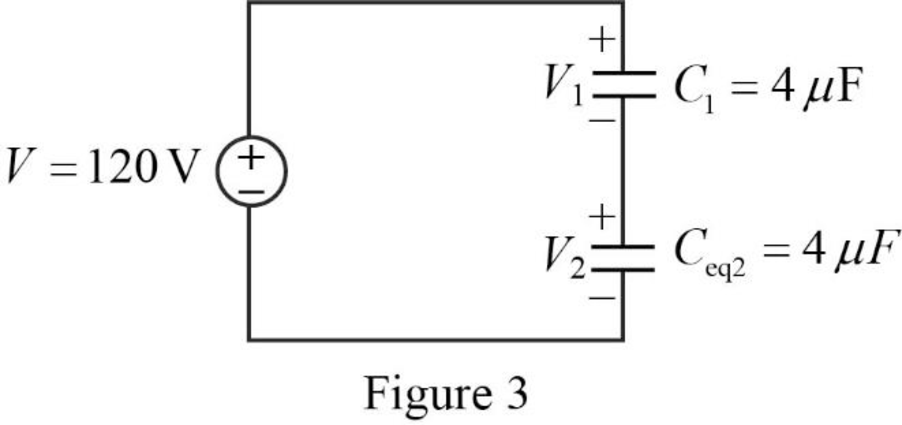
Write the expression to calculate the total applied voltage.

$V=V_1+V_2$        (4)

Here,

$V_1$ is the voltage across the capacitor 1, and

$V_2$ is the voltage across the equivalent capacitor 2.

From the Figure 3, it is clear that the voltage across the capacitors with same capacitance value is equal. Therefore,

$V_1=V_2$        (5)

Substitute $120\text{V}$ for $V$ and $V_1$ for $V_2$ in equation (4).

$\begin{array}{c}120\text{V}=V_1+V_1\\ =2V_1\end{array}$

Simplify the above equation to find $V_1$.

$\begin{array}{c}{V}_1=\frac{120\text{V}}{2}\\ =60\text{V}\end{array}$

Therefore, from equation (5),

$V_1=V_2=60\text{V}$

Write the expression to calculate the charge across the capacitor 1.

$q_1=C_1{V}_1$        (6)

Here,

$C_1$ is the value of the capacitor 1.

Substitute $4\mu \text{F}$ for $C_1$ and $60\text{V}$ for $V_1$ in equation (6) to find $q_1$.

$\begin{array}{c}{q}_1=\left(4\mu \text{F}\right)\left(60\text{V}\right)\\ =\left(4\times {10}^{-6}\right)\left(60\right)\text{F}\cdot \text{V}\left\{\because 1\mu ={10}^{-6}\right\}\\ =0.24\times {10}^{-3}\left(\frac{\text{C}}{\text{V}}\right)\cdot \text{V}\left\{\because \text{1F}=\frac{1\text{C}}{1\text{V}}\right\}\\ =0.24\text{mC}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Write the expression to calculate the charge across the capacitor 2.

$q_2=C_2{V}_2$        (7)

Substitute $2\mu \text{F}$ for $C_2$ and $60\text{V}$ for $V_2$ in equation (7) to find $q_2$.

$\begin{array}{c}{q}_2=\left(2\mu \text{F}\right)\left(60\text{V}\right)\\ =\left(2\times {10}^{-6}\right)\left(60\right)\text{F}\cdot \text{V}\left\{\because 1\mu ={10}^{-6}\right\}\\ =0.12\times {10}^{-3}\left(\frac{\text{C}}{\text{V}}\right)\cdot \text{V}\left\{\because \text{1F}=\frac{1\text{C}}{1\text{V}}\right\}\\ =0.12\text{mC}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Refer to Figure 2, the capacitors $C_2$ and $C_{\text{eq1}}$ are connected in parallel form. For parallel connection, the voltage is same. Here, the capacitors $C_2$ and $C_{\text{eq1}}$ have same capacitance value and voltage, therefore the charge of the capacitors should be same that is charge $q_2$.

The combination of the series connected capacitors $C_3$ and $C_4$ is $C_{\text{eq1}}$. For series connection, the charge is same. Therefore, the charge for the capacitors $C_3$ and $C_4$ is same as $C_{\text{eq1}}$ that is $q_2$.

$q_2=q_3=q_4$

Write the expression to calculate the voltage across the capacitor 3.

$V_3=\frac{q_2}{C_3}$        (8)

Substitute $0.12\text{mC}$ for $q_2$ and $6\mu \text{F}$ for $C_3$ in equation (8) to find $V_3$.

$\begin{array}{c}{V}_3=\frac{0.12\text{mC}}{6\mu \text{F}}\\ =\frac{0.12\times {10}^{-3}}{6\times {10}^{-6}}\frac{\text{C}}{\text{F}}\left\{\because 1\text{m}={10}^{-3},1\mu ={10}^{-6}\right\}\\ =20\left(\frac{\text{V}\cdot \text{F}}{\text{F}}\right)\left\{\because \text{1}\text{C}=1\text{V}\cdot \text{1}\text{F}\right\}\\ =20\text{V}\end{array}$

Write the expression to calculate the voltage across the capacitor 4.

$V_4=\frac{q_2}{C_4}$        (9)

Substitute $0.12\text{mC}$ for $q_2$ and $3\mu \text{F}$ for $C_4$ in equation (9) to find $V_4$.

$\begin{array}{c}{V}_4=\frac{0.12\text{mC}}{3\mu \text{F}}\\ =\frac{0.12\times {10}^{-3}}{3\times {10}^{-6}}\frac{\text{C}}{\text{F}}\left\{\because 1\text{m}={10}^{-3},1\mu ={10}^{-6}\right\}\\ =40\left(\frac{\text{V}\cdot \text{F}}{\text{F}}\right)\left\{\because \text{1}\text{C}=1\text{V}\cdot \text{1}\text{F}\right\}\\ =40\text{V}\left\{\because 1\text{V}=\frac{\text{1C}}{\text{1F}}\right\}\end{array}$

Re-write the equation (1) to calculate the energy stored in capacitor $1$.

$w_1=\frac{1}{2}{C}_1{V}_1{}^2$

Substitute $4\mu \text{F}$ for $C_1$ and $60\text{V}$ for $V_1$ in above equation to find $w_1$.

$\begin{array}{c}{w}_1=\frac{1}{2}\left(4\mu \text{F}\right){\left(60\text{V}\right)}^2\\ =\frac{1}{2}\left(4\times {10}^{-6}\right){\left(60\right)}^2\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =7.2\times {10}^{-3}\left(\frac{\text{J}}{{\text{V}}^2}\right)\cdot {\text{V}}^2\left\{\because 1\text{F}=\frac{1\text{J}}{1{\text{V}}^2}\right\}\\ =7.2\text{mJ}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Re-write the equation (1) to calculate the energy stored in capacitor $2$.

$w_2=\frac{1}{2}{C}_2{V}_2{}^2$

Substitute $2\mu \text{F}$ for $C_2$ and $60\text{V}$ for $V_2$ in above equation to find $w_2$.

$\begin{array}{c}{w}_2=\frac{1}{2}\left(2\mu \text{F}\right){\left(60\text{V}\right)}^2\\ =\frac{1}{2}\left(2\times {10}^{-6}\right){\left(60\right)}^2\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =3.6\times {10}^{-3}\left(\frac{\text{J}}{{\text{V}}^2}\right)\cdot {\text{V}}^2\left\{\because 1\text{F}=\frac{1\text{J}}{1{\text{V}}^2}\right\}\\ =3.6\text{mJ}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Re-write the equation (1) to calculate the energy stored in capacitor $3$.

$w_3=\frac{1}{2}{C}_3{V}_3{}^2$

Substitute $6\mu \text{F}$ for $C_3$ and $20\text{V}$ for $V_3$ in above equation to find $w_3$.

$\begin{array}{c}{w}_3=\frac{1}{2}\left(6\mu \text{F}\right){\left(20\text{V}\right)}^2\\ =\frac{1}{2}\left(6\times {10}^{-6}\right){\left(20\right)}^2\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =1.2\times {10}^{-3}\left(\frac{\text{J}}{{\text{V}}^2}\right)\cdot {\text{V}}^2\left\{\because 1\text{F}=\frac{1\text{J}}{1{\text{V}}^2}\right\}\\ =1.2\text{mJ}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Re-write the equation (1) to calculate the energy stored in capacitor $4$.

$w_4=\frac{1}{2}{C}_4{V}_4{}^2$

Substitute $3\mu \text{F}$ for $C_4$ and $40\text{V}$ for $V_4$ in above equation to find $w_4$.

$\begin{array}{c}{w}_4=\frac{1}{2}\left(3\mu \text{F}\right){\left(40\text{V}\right)}^2\\ =\frac{1}{2}\left(3\times {10}^{-6}\right){\left(40\right)}^2\text{F}\cdot {\text{V}}^2\left\{\because 1\mu ={10}^{-6}\right\}\\ =2.4\times {10}^{-3}\left(\frac{\text{J}}{{\text{V}}^2}\right)\cdot {\text{V}}^2\left\{\because 1\text{F}=\frac{1\text{J}}{1{\text{V}}^2}\right\}\\ =2.4\text{mJ}\left\{\because 1\text{m}={10}^{-3}\right\}\end{array}$

Therefore, the value of the voltage across the capacitor 1 $V_1$ is $60\text{V}$, the capacitor 2 $V_2$ is $60\text{V}$, the capacitor 3 $V_3$ is $20\text{V}$ and the capacitor 4 $V_4$ is $40\text{V}$ and the energy stored in capacitor 1 $w_1$ is $7.2\text{mJ}$, the capacitor 2 $w_2$ is $3.6\text{mJ}$, the capacitor 3 $w_3$ is $1.2\text{mJ}$ and the capacitor 4 $w_4$ is $2.4\text{mJ}$.

Conclusion:

Thus, the problem to make better understand how capacitors work together when connected in series and in parallel using Figure 6.57 is designed.