
Concept explainers
a.
Construct the
Calculate the mean and standard deviation of this distribution.
a.
Answer to Problem 70DA
The probability distributions for the number of bedrooms are as follows:
| Number of Bedrooms | Frequency |
Probability |
| 2 | 24 | 0.2286 |
| 3 | 26 | 0.2476 |
| 4 | 26 | 0.2476 |
| 5 | 11 | 0.1048 |
| 6 | 14 | 0.1333 |
| 7 | 2 | 0.0190 |
| 8 | 2 | 0.0190 |
| Total | 105 | 1 |
The mean of the distribution is 3.8.
The standard deviation of the distribution is 1.4954.
Explanation of Solution
Step-by-step procedure to obtain the frequency table for bedrooms using EXCEL:
- Enter the data in an EXCEL sheet.
- Go to Insert > PivotTable > PivotTable.
- In Table/
Range , select the column Bedrooms and click OK. - In PivotTable Field List, drag Bedrooms to Row Labels and to ∑ values.
- Click on it from ∑ values.
- Choose Value Field Settings.
- In Summarize value field by, choose Count and click OK.
The output obtained is as follows:
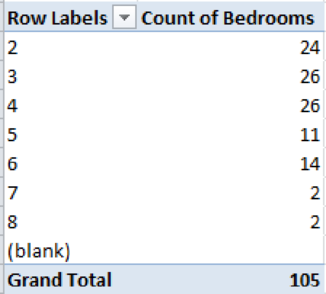
The probability distributions for the number of bedrooms are calculated as follows:
| Number of Bedrooms | Frequency |
Probability |
| 2 | 24 | |
| 3 | 26 | |
| 4 | 26 | |
| 5 | 11 | |
| 6 | 14 | |
| 7 | 2 | |
| 8 | 2 | |
| Total | 105 | 1 |
The mean of the distribution is calculated as follows:
Therefore, the mean of the distribution is 3.8.
Consider the following table that shows preliminary calculations to compute the standard deviation:
| Bedrooms | Frequency |
Probability | ||
| 2 | 24 | 0.2286 | ||
| 3 | 26 | 0.2476 | ||
| 4 | 26 | 0.2476 | ||
| 5 | 11 | 0.1048 | ||
| 6 | 14 | 0.1333 | ||
| 7 | 2 | 0.0190 | ||
| 8 | 2 | 0.0190 | ||
| 105 | 2.2362 |
The standard deviation of the distribution is calculated as follows:
Therefore, the standard deviation of the distribution is 1.4954.
b.
Construct the probability distribution for the number of bathrooms.
Find the mean and standard deviation for this distribution.
b.
Answer to Problem 70DA
The probability distributions for the number of bathrooms are as follows:
| Number of Bathrooms | Frequency |
Probability |
| 1.5 | 24 | 0.2286 |
| 2 | 17 | 0.1619 |
| 2.5 | 13 | 0.1238 |
| 3 | 22 | 0.2095 |
| 3.5 | 11 | 0.1048 |
| 4 | 11 | 0.1048 |
| 4.5 | 3 | 0.0286 |
| 5 | 2 | 0.0190 |
| 5.5 | 2 | 0.0190 |
| 105 |
The mean of the distribution is 2.7189.
The standard deviation of the distribution is 1.0093.
Explanation of Solution
Step-by-step procedure to obtain the frequency table for bedrooms using EXCEL:
- Enter the data in an EXCEL sheet.
- Go to Insert > PivotTable > PivotTable.
- In Table/Range, select the column Bathrooms and click OK.
- In PivotTable Field List, drag Bathrooms to Row Labels and to ∑ values.
- Click on it from ∑ values.
- Choose Value Field Settings.
- In Summarize value field by, choose Count and click OK.
The output obtained is as follows:
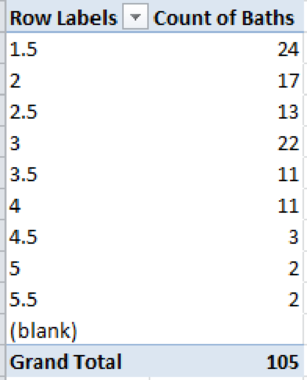
The probability distributions for the number of bathrooms are calculated as follows:
| Number of Bathrooms | Frequency |
Probability |
| 1.5 | 24 | |
| 2 | 17 | |
| 2.5 | 13 | |
| 3 | 22 | |
| 3.5 | 11 | |
| 4 | 11 | |
| 4.5 | 3 | |
| 5 | 2 | |
| 5.5 | 2 | |
| Total | 105 | 1 |
The mean of the distribution is calculated as follows:
Therefore, the mean of the distribution is 2.7189.
Consider the following table that shows preliminary calculations to compute the standard deviation:
| Number of Bathrooms | Frequency |
Probability | ||
| 1.5 | 24 | 0.2286 | ||
| 2 | 17 | 0.1619 | ||
| 2.5 | 13 | 0.1238 | ||
| 3 | 22 | 0.2095 | ||
| 3.5 | 11 | 0.1048 | ||
| 4 | 11 | 0.1048 | ||
| 4.5 | 3 | 0.0286 | ||
| 5 | 2 | 0.0190 | ||
| 5.5 | 2 | 0.0190 | ||
| Total | 105 |
The standard deviation of the distribution is calculated as follows:
Therefore, the standard deviation of the distribution is 1.0093.
Want to see more full solutions like this?
Chapter 6 Solutions
Gen Combo Ll Statistical Techniques In Business And Economics; Connect Ac
- Client 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127arrow_forwardClient 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127 a) Determine the mean change in patient weight from before to after the diet (after – before). What is the 95% confidence interval of this mean difference?arrow_forwardIn order to find probability, you can use this formula in Microsoft Excel: The best way to understand and solve these problems is by first drawing a bell curve and marking key points such as x, the mean, and the areas of interest. Once marked on the bell curve, figure out what calculations are needed to find the area of interest. =NORM.DIST(x, Mean, Standard Dev., TRUE). When the question mentions “greater than” you may have to subtract your answer from 1. When the question mentions “between (two values)”, you need to do separate calculation for both values and then subtract their results to get the answer. 1. Compute the probability of a value between 44.0 and 55.0. (The question requires finding probability value between 44 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 44, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the…arrow_forward
- If a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9. The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24? The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by creating a chart. Clearly mark the range, identifying the lower and upper…arrow_forwardProblem 1: The mean hourly pay of an American Airlines flight attendant is normally distributed with a mean of 40 per hour and a standard deviation of 3.00 per hour. What is the probability that the hourly pay of a randomly selected flight attendant is: Between the mean and $45 per hour? More than $45 per hour? Less than $32 per hour? Problem 2: The mean of a normal probability distribution is 400 pounds. The standard deviation is 10 pounds. What is the area between 415 pounds and the mean of 400 pounds? What is the area between the mean and 395 pounds? What is the probability of randomly selecting a value less than 395 pounds? Problem 3: In New York State, the mean salary for high school teachers in 2022 was 81,410 with a standard deviation of 9,500. Only Alaska’s mean salary was higher. Assume New York’s state salaries follow a normal distribution. What percent of New York State high school teachers earn between 70,000 and 75,000? What percent of New York State high school…arrow_forwardPls help asaparrow_forward
- Solve the following LP problem using the Extreme Point Theorem: Subject to: Maximize Z-6+4y 2+y≤8 2x + y ≤10 2,y20 Solve it using the graphical method. Guidelines for preparation for the teacher's questions: Understand the basics of Linear Programming (LP) 1. Know how to formulate an LP model. 2. Be able to identify decision variables, objective functions, and constraints. Be comfortable with graphical solutions 3. Know how to plot feasible regions and find extreme points. 4. Understand how constraints affect the solution space. Understand the Extreme Point Theorem 5. Know why solutions always occur at extreme points. 6. Be able to explain how optimization changes with different constraints. Think about real-world implications 7. Consider how removing or modifying constraints affects the solution. 8. Be prepared to explain why LP problems are used in business, economics, and operations research.arrow_forwardged the variance for group 1) Different groups of male stalk-eyed flies were raised on different diets: a high nutrient corn diet vs. a low nutrient cotton wool diet. Investigators wanted to see if diet quality influenced eye-stalk length. They obtained the following data: d Diet Sample Mean Eye-stalk Length Variance in Eye-stalk d size, n (mm) Length (mm²) Corn (group 1) 21 2.05 0.0558 Cotton (group 2) 24 1.54 0.0812 =205-1.54-05T a) Construct a 95% confidence interval for the difference in mean eye-stalk length between the two diets (e.g., use group 1 - group 2).arrow_forwardAn article in Business Week discussed the large spread between the federal funds rate and the average credit card rate. The table below is a frequency distribution of the credit card rate charged by the top 100 issuers. Credit Card Rates Credit Card Rate Frequency 18% -23% 19 17% -17.9% 16 16% -16.9% 31 15% -15.9% 26 14% -14.9% Copy Data 8 Step 1 of 2: Calculate the average credit card rate charged by the top 100 issuers based on the frequency distribution. Round your answer to two decimal places.arrow_forward
- Please could you check my answersarrow_forwardLet Y₁, Y2,, Yy be random variables from an Exponential distribution with unknown mean 0. Let Ô be the maximum likelihood estimates for 0. The probability density function of y; is given by P(Yi; 0) = 0, yi≥ 0. The maximum likelihood estimate is given as follows: Select one: = n Σ19 1 Σ19 n-1 Σ19: n² Σ1arrow_forwardPlease could you help me answer parts d and e. Thanksarrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL



