
Concept explainers
A golfer tees off from a location precisely at ϕi = 35.0° north latitude. He hits the ball due south, with range 285 m. The ball’s initial velocity is at 48.0° above the horizontal. Suppose air resistance is negligible for the golf ball. (a) For how long is the ball in flight? The cup is due south of the golfer’s location, and the golfer would have a hole-in-one if the Earth were not rotating. The Earth’s rotation makes the tee move in a circle of radius RE cos ϕi = (6.37 × 106 m) cos 35.0° as shown in Figure P6.47. The tee completes one revolution each day. (b) Find the eastward speed of the tee relative to the stars. The hole is also moving cast, but it is 285 m farther south and thus at a slightly lower latitude ϕf. Because the hole moves in a slightly larger circle, its speed must he greater than that of the tee. (c) By how much does the hole’s speed exceed that of the tee? During the time interval the ball is in flight, it moves upward and downward as well as southward with the projectile motion you studied in Chapter 4, but it also moves eastward with the speed you found in part (b). The hole moves to the east at a faster speed, however, pulling ahead of the ball with the relative speed you found in part (c). (d) How far to the west of the hole does the ball land?
Figure P6.47
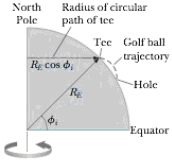
(a)
The time of flight of the ball.
Answer to Problem 47CP
The time for which the ball be in flight is
Explanation of Solution
The range of the motion after hitting the ball is
The range of the parabolic motion
Here,
Write the expression for the equation for parabolic motion
As initial and final distance is equal,
Rearrange the above expression for
Substitute
Rearrange the above expression for
Substitute
Conclusion:
Substitute
Therefore, the time for which the ball be in flight is
(b)
The relative eastward speed of the tee with respect to the stars.
Answer to Problem 47CP
The relative eastward speed of the tee with respect to the stars is
Explanation of Solution
Write the formula to calculate the eastward speed of the tee relative to the stars
Here,
Conclusion:
Substitute
Therefore, the relative eastward speed of the tee with respect to the stars is
(c)
The value by which the hole's speed exceed that of the tee.
Answer to Problem 47CP
The value by which the hole's speed exceed that of the tee is
Explanation of Solution
Write the formula to calculate the length of the arc
Rearrange the above expression for
Substitute
Write the formula to calculate the speed of the hole
Here,
Substitute
Calculate the difference between the speed of tee and the speed of hole.
Here,
Conclusion:
Substitute
Therefore, the value by which the hole's speed exceed that of the tee is
(d)
The distance to the west of the hole from the position where the ball lands.
Answer to Problem 47CP
The distance to the west of the hole from the position where the ball land is
Explanation of Solution
Write the expression for the distance to west of the hole
Here,
Conclusion:
Substitute
Therefore, the distance to the west of the hole from the position where the ball land is
Want to see more full solutions like this?
Chapter 6 Solutions
PHYSICS FOR SCI.AND ENGR W/WEBASSIGN
- No chatgpt pls will upvote Iarrow_forwardHow would partial obstruction of an air intake port of an air-entrainment mask effect FiO2 and flow?arrow_forward14 Z In figure, a closed surface with q=b= 0.4m/ C = 0.6m if the left edge of the closed surface at position X=a, if E is non-uniform and is given by € = (3 + 2x²) ŷ N/C, calculate the (3+2x²) net electric flux leaving the closed surface.arrow_forward
- No chatgpt pls will upvotearrow_forwardsuggest a reason ultrasound cleaning is better than cleaning by hand?arrow_forwardCheckpoint 4 The figure shows four orientations of an electric di- pole in an external electric field. Rank the orienta- tions according to (a) the magnitude of the torque on the dipole and (b) the potential energy of the di- pole, greatest first. (1) (2) E (4)arrow_forward
- What is integrated science. What is fractional distillation What is simple distillationarrow_forward19:39 · C Chegg 1 69% ✓ The compound beam is fixed at Ę and supported by rollers at A and B. There are pins at C and D. Take F=1700 lb. (Figure 1) Figure 800 lb ||-5- F 600 lb بتا D E C BO 10 ft 5 ft 4 ft-—— 6 ft — 5 ft- Solved Part A The compound beam is fixed at E and... Hình ảnh có thể có bản quyền. Tìm hiểu thêm Problem A-12 % Chia sẻ kip 800 lb Truy cập ) D Lưu of C 600 lb |-sa+ 10ft 5ft 4ft6ft D E 5 ft- Trying Cheaa Những kết quả này có hữu ích không? There are pins at C and D To F-1200 Egue!) Chegg Solved The compound b... Có Không ☑ ||| Chegg 10 וחarrow_forwardNo chatgpt pls will upvotearrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





