
Concept explainers
Find the slope
Answer to Problem 33P
The slope
The deflection
The slope
The deflection
Explanation of Solution
Given information:
The Young’s modulus (E) is 29,000 ksi.
The moment of inertia (I) is
Calculation:
Consider flexural rigidity EI of the beam is constant.
Show the free body diagram of the given beam as in Figure (1).
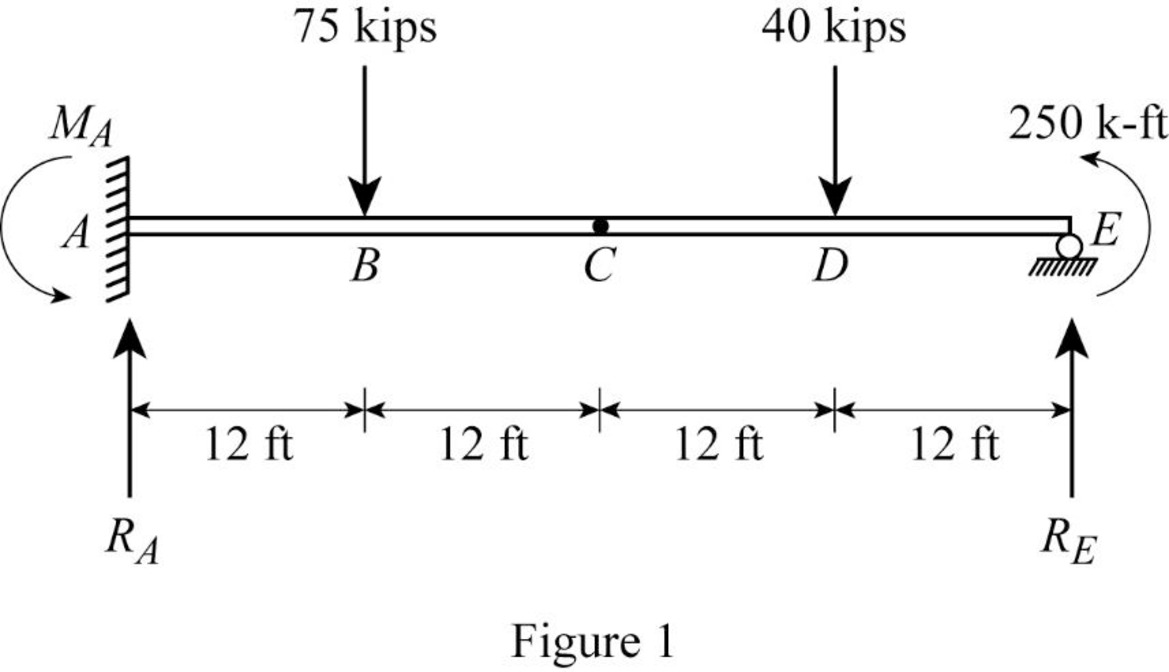
Refer Figure (1),
Consider upward is force is positive and downward force is negative.
Consider clockwise moment is negative and counterclockwise moment is positive.
Split the given beam into two sections such as AC and CE.
Consider the portion CE:
Draw the free body diagram of the portion CE as in Figure (2).
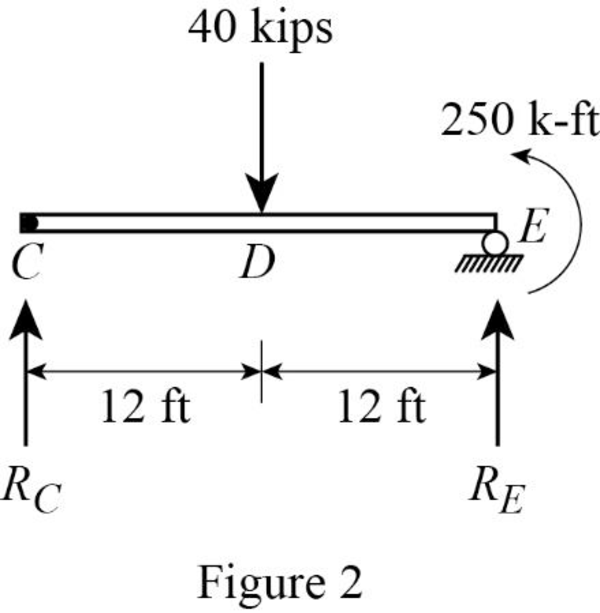
Refer Figure (2),
Consider a reaction at C and take moment about point C.
Determine the reaction at E;
Determine the reaction at support A;
Show the reaction of the given beam as in Figure (3).
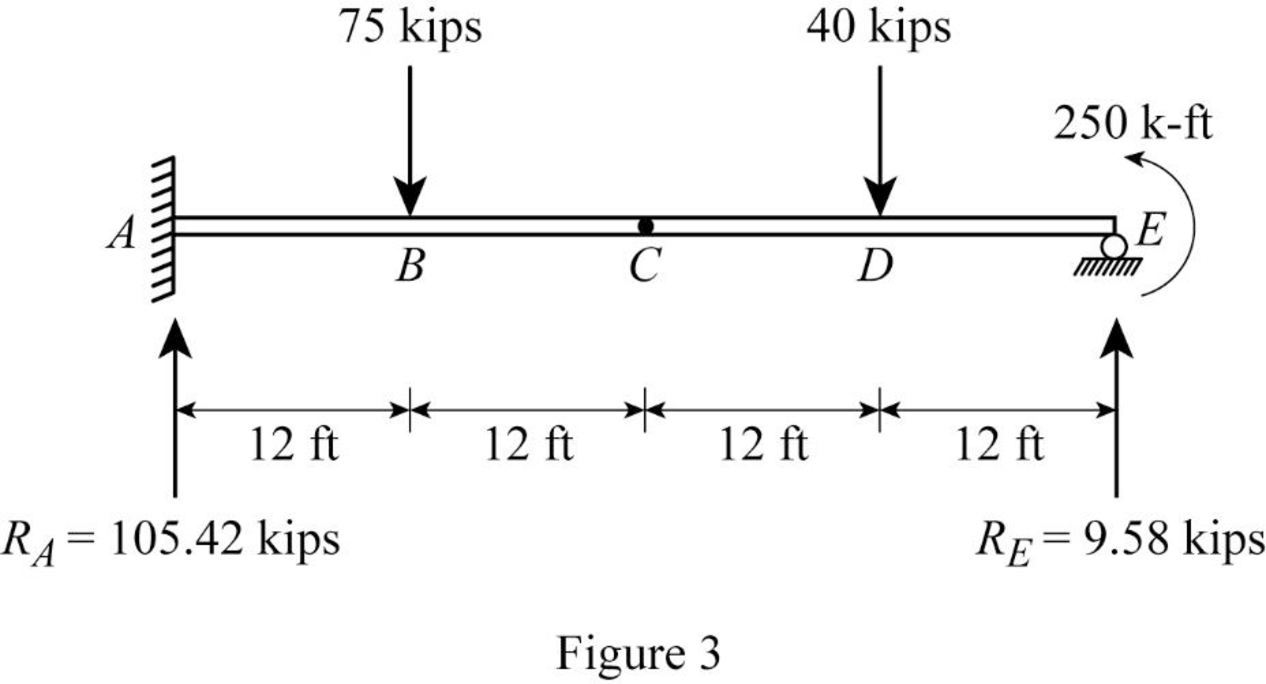
Refer Figure (3),
Determine the moment at A:
Determine the bending moment at B;
Determine the bending moment at C;
Determine the bending moment at D;
Determine the bending moment at E;
Show the
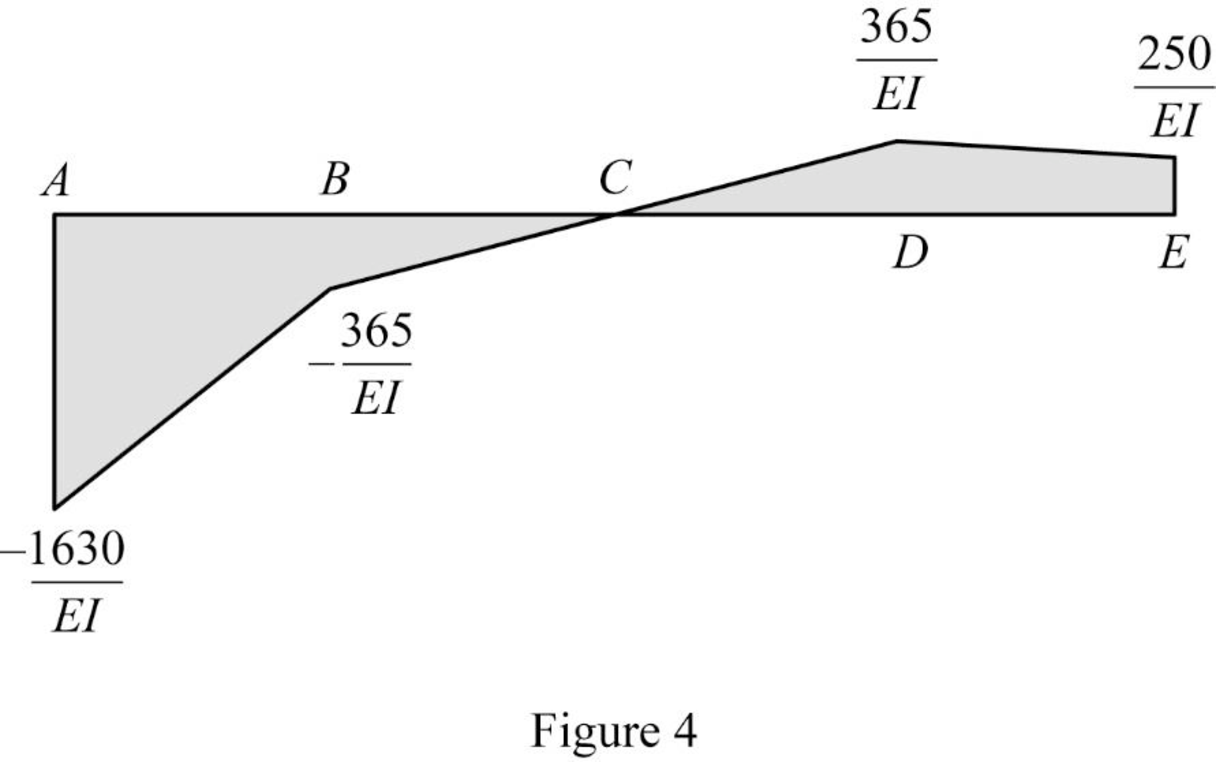
Show the elastic curve diagram as in Figure (5).
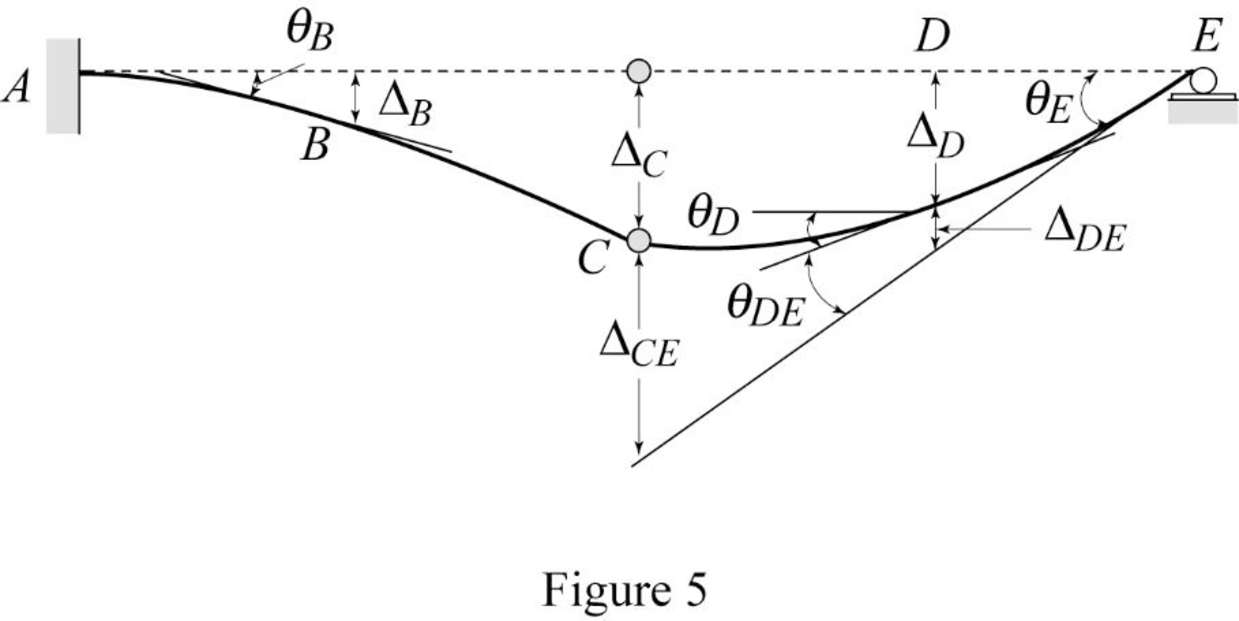
Refer Figure (4),
Determine the slope at B;
Here, b is the width and h is the height of respective triangle.
Substitute 12 ft for
Substitute 29,000 ksi for E and
Hence, the slope at B is
Determine the deflection between A and B using the relation;
Here,
Substitute 12 ft for
Substitute 29,000 ksi for E and
Hence, the deflection at B is
To determine the slope at point E, it is necessary to determine the deflection at point C and the deflection between C and E.
Determine the deflection at C and A using the relation;
Substitute 12 ft for
Determine the deflection between C and E using the relation;
Substitute 12 ft for
Determine the slope at E using the relation;
Here,
Substitute
Determine the slope between D and E using the relation;
Here, b is the width and h is the height of respective triangle.
Substitute 12 ft for
Determine the slope at D using the relation;
Substitute
Substitute 29,000 ksi for E and
Hence, the slope at D is
Determine the deflection between D and E using the relation;
Here, b is the width and h is the height of respective rectangle and triangle.
Substitute 12 ft for
Determine the deflection at D using the relation;
Substitute 12 ft for
Substitute 29,000 ksi for E and
Hence, the deflection at point D is
Want to see more full solutions like this?
Chapter 6 Solutions
Structural Analysis
- 6000 units have been installed to date with 9,000 units to install. Labor costs are $23,300.00 to date. What is the unit cost for labor to date?arrow_forwardThe base rate for labor is $15/hr. The labor burden is 35% and 3% for small tools for the labor. There are 1000 units to install. Records indicate that trade workers can install 10 units per hour, per trade worker. The owners need 15% overhead and profit to pay bills, pay interest on loan and provide some profit to the partners. What is the minimum bid assuming no risk avoidance factor?arrow_forwardCan you show me how to obtain these answers thanks, will rate!arrow_forward
- I have the answers for part a just need help with b mostly thanksarrow_forwardPlease explain step by step and show formulasarrow_forward5. (20 Points) Consider a channel width change in the same 7-foot wide rectangular in Problem 4. The horizontal channel narrows as depicted below. The flow rate is 90 cfs, and the energy loss (headloss) through the transition is 0.05 feet. The water depth at the entrance to the transition is initially 4'. 1 b₁ TOTAL ENERGY LINE V² 129 У1 I b₂ TOP VIEW 2 PROFILE VIEW h₁ = 0.05 EGL Y₂ = ? a) b) c) 2 Determine the width, b₂ that will cause a choke at location 2. Determine the water depth at the downstream end of the channel transition (y₂) section if b₂ = 5 feet. Calculate the change in water level after the transition. Plot the specific energy diagram showing all key points. Provide printout in homework. d) What will occur if b₂ = = 1.5 ft.?arrow_forward
- 4. (20 Points) A transition section has been proposed to raise the bed level a height Dz in a 7-foot wide rectangular channel. The design flow rate in the channel is 90 cfs, and the energy loss (headloss) through the transition is 0.05 feet. The water depth at the entrance to the transition section is initially 4 feet. b₁ = b = b2 1 TOTAL ENERGY LINE V² 129 Ут TOP VIEW 2 hloss = 0.05 " EGL Y₂ = ? PROFILE VIEW a) Determine the minimum bed level rise, Dz, which will choke the flow. b) If the step height, Dz = 1 ft, determine the water depth (y2) at the downstream end of the channel transition section. Calculate the amount the water level drops or rises over the step. c) Plot the specific energy diagram showing all key points. Provide printout in Bework. d) What will occur if Dz = 3.0 ft.?. Crest Front Viewarrow_forward1. (20 Points) Determine the critical depth in the trapezoidal drainage ditch shown below. The slope of the ditch is 0.0016, the side slopes are 1V:2.5H, the bottom width is b = 14', and the design discharge is 500 cfs. At this discharge the depth is y = 4.25'. Also, determine the flow regime and calculate the Froude number. Ye= ? Z barrow_forward3. (20 Points) A broad crested weir, 10 feet high, will be constructed in a rectangular channel B feet wide. The weir crest extends a length of B = 120 feet between the banks with 2 - 4 foot wide, round nosed piers in the channel. The width of the weir crest is 8 feet. If H = 6', determine the design discharge for the weir.arrow_forward
