Physics for Scientists and Engineers with Modern Physics
10th Edition
ISBN: 9781337553292
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6, Problem 28AP
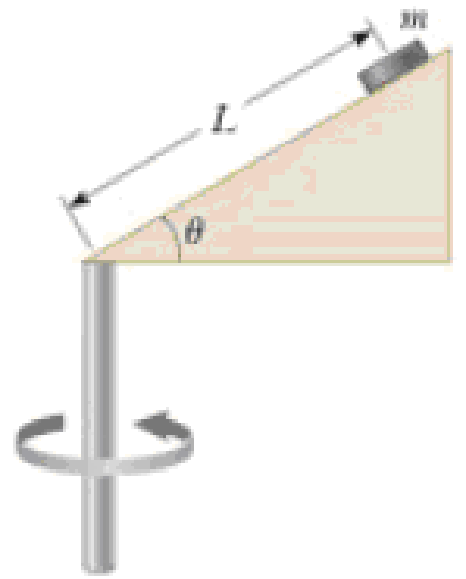
A child’s toy consists of a small wedge that has an acute angle θ (Fig. P6.28). The sloping side of the wedge is frictionless, and an object of mass m on it remains at constant height if the wedge is spun at a certain constant speed. The wedge is spun by rotating, as an axis, a vertical rod that is firmly attached to the wedge at the bottom end. Show that, when the object sits at rest at a point at distance L up along the wedge, the speed of the object must be v = (gL sin θ)1/2.
Figure P6.28
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The force of the quadriceps (Fq) and force of the patellar tendon (Fp) is identical (i.e., 1000 N each). In the figure below angle in blue is Θ and the in green is half Θ (i.e., Θ/2). A) Calculate the patellar reaction force (i.e., R resultant vector is the sum of the horizontal component of the quadriceps and patellar tendon force) at the following joint angles: you need to provide a diagram showing the vector and its components for each part. a1) Θ = 160 degrees, a2) Θ = 90 degrees. NOTE: USE DO NOT USE LAW OF COSINES, NO COMPLICATED ALGEBRAIC EQUATIONS OR ANYTHING ELSE, ETC. Question A has 2 parts!
No chatgpt pls will upvote
The force of the quadriceps (Fq) and force of the patellar tendon (Fp) is identical (i.e., 1000 N each). In the figure below angle in blue is Θ and the in green is half Θ (i.e., Θ/2). A) Calculate the patellar reaction force (i.e., R resultant vector is the sum of the horizontal component of the quadriceps and patellar tendon force) at the following joint angles: you need to provide a diagram showing the vector and its components for each part. a1) Θ = 160 degrees, a2) Θ = 90 degrees. NOTE: USE ONLY TRIGNOMETRIC FUNCTIONS (SIN/TAN/COS, NO LAW OF COSINES, NO COMPLICATED ALGEBRAIC EQUATIONS OR ANYTHING ELSE, ETC. Question A has 2 parts!
Chapter 6 Solutions
Physics for Scientists and Engineers with Modern Physics
Ch. 6.1 - You are riding on a Ferris wheel that is rotating...Ch. 6.2 - A bead slides at constant speed along a curved...Ch. 6.3 - Consider the passenger in the car making a left...Ch. 6.4 - A basketball and a 2-inch-diameter steel ball,...Ch. 6 - In the Bohr model of the hydrogen atom, an...Ch. 6 - Whenever two Apollo astronauts were on the surface...Ch. 6 - A car initially traveling eastward turns north by...Ch. 6 - A curve in a road forms part of a horizontal...Ch. 6 - In a cyclotron (one type of particle accelerator),...Ch. 6 - Why is the following situation impossible? The...
Ch. 6 - You are working during your summer break as an...Ch. 6 - Prob. 8PCh. 6 - Prob. 9PCh. 6 - A 40.0-kg child swings in a swing supported by two...Ch. 6 - Prob. 11PCh. 6 - One end of a cord is fixed and a small 0.500-kg...Ch. 6 - A roller coaster at the Six Flags Great America...Ch. 6 - An object of mass m = 5.00 kg, attached to a...Ch. 6 - A person stands on a scale in an elevator. As the...Ch. 6 - Review. A student, along with her backpack on the...Ch. 6 - A small container of water is placed on a...Ch. 6 - The mass of a sports car is 1 200 kg. The shape of...Ch. 6 - Review. A window washer pulls a rubber squeegee...Ch. 6 - A small piece of Styrofoam packing material is...Ch. 6 - Prob. 21PCh. 6 - Assume the resistive force acting on a speed...Ch. 6 - You can feel a force of air drag on your hand if...Ch. 6 - A car travels clockwise at constant speed around a...Ch. 6 - A string under a tension of 50.0 N is used to...Ch. 6 - Disturbed by speeding cars outside his workplace,...Ch. 6 - A car of mass m passes over a hump in a road that...Ch. 6 - A childs toy consists of a small wedge that has an...Ch. 6 - A seaplane of total mass m lands on a lake with...Ch. 6 - An object of mass m1 = 4.00 kg is tied to an...Ch. 6 - A ball of mass m = 0.275 kg swings in a vertical...Ch. 6 - Why is the following situation impossible? A...Ch. 6 - The pilot of an airplane executes a loop-the-loop...Ch. 6 - A basin surrounding a drain has the shape of a...Ch. 6 - Review. While learning to drive, you arc in a 1...Ch. 6 - A truck is moving with constant acceleration a up...Ch. 6 - Prob. 37APCh. 6 - A puck of mass m1 is tied to a string and allowed...Ch. 6 - Prob. 39APCh. 6 - Members of a skydiving club were given the...Ch. 6 - A car rounds a banked curve as discussed in...Ch. 6 - Prob. 42APCh. 6 - Review. A piece of putty is initially located at...Ch. 6 - A model airplane of mass 0.750 kg flies with a...Ch. 6 - A 9.00-kg object starting from rest falls through...Ch. 6 - For t 0, an object of mass m experiences no force...Ch. 6 - A golfer tees off from a location precisely at i =...Ch. 6 - A single bead can slide with negligible friction...Ch. 6 - Prob. 49CPCh. 6 - You have a great job working at a major league...
Additional Science Textbook Solutions
Find more solutions based on key concepts
1. Rub your hands together vigorously. What happens? Discuss the energy transfers and transformations that take...
College Physics: A Strategic Approach (3rd Edition)
Separate the list P,F,V,,T,a,m,L,t, and V into intensive properties, extensive properties, and nonproperties.
Fundamentals Of Thermodynamics
Give the IUPAC name for each compound.
Organic Chemistry
Choose the best answer to each of the following. Explain your reasoning. If Earth were twice as far as it actua...
Cosmic Perspective Fundamentals
Q1. What is the empirical formula of a compound with the molecular formula
Chemistry: A Molecular Approach (4th Edition)
An obese 55-year-old woman consults her physician about minor chest pains during exercise. Explain the physicia...
Biology: Life on Earth with Physiology (11th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- ་ The position of a particle is described by r = (300e 0.5t) mm and 0 = (0.3t²) rad, where t is in seconds. Part A Determine the magnitude of the particle's velocity at the instant t = 1.5 s. Express your answer to three significant figures and include the appropriate units. v = Value Submit Request Answer Part B ? Units Determine the magnitude of the particle's acceleration at the instant t = 1.5 s. Express your answer to three significant figures and include the appropriate units. a = Value A ? Unitsarrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forward
- A spiral transition curve is used on railroads to connect a straight portion of the track with a curved portion. (Figure 1) Part A v = v₁ft/s 600 ft y = (106) x³ If the spiral is defined by the equation y = (106)³, where x and y are in feet, determine the magnitude of the acceleration of a train engine moving with a constant speed of v₁ = 30 ft/s when it is at point x = 600 ft. Express your answer to three significant figures and include the appropriate units. ? a = Value Unitsarrow_forwardsolve and answer the problem correctly please. Thank you!!arrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forward
- Solve and answer the question correctly please. Thank you!!arrow_forwardWhen the motorcyclist is at A, he increases his speed along the vertical circular path at the rate of = (0.3t) ft/s², where t is in seconds. Take p = 360 ft. (Figure 1) Part A 60° Ρ B If he starts from rest at A, determine the magnitude of his velocity when he reaches B. Express your answer to three significant figures and include the appropriate units. v = Value Submit Request Answer ་ Part B ? Units If he starts from rest at A, determine the magnitude of his acceleration when he reaches B. Express your answer to three significant figures and include the appropriate units. 11 ? a = Value Unitsarrow_forwardThe car starts from rest at s = 0 and increases its speed at a₁ = 7 m/s². (Figure 1) Part A = 40 m Determine the time when the magnitude of acceleration becomes 20 m/s². Express your answer to three significant figures and include the appropriate units. ? t = Value Units Part B At what position s does this occur? Express your answer to three significant figures and include the appropriate units. s = Value Submit Request Answer ? Unitsarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
Gravitational Force (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=pxp1Z91S5uQ;License: Standard YouTube License, CC-BY