Chapter 5.4, Problem 5.123P

Determine by direct integration the values of $\bar{x}$ for the two volumes obtained by passing a vertical cutting plane through the given shape of Figure 5.21. The cutting plane is parallel to the base of the given shape and divides the shape into two volumes of equal height.

A semiellipsoid of revolution

To determine

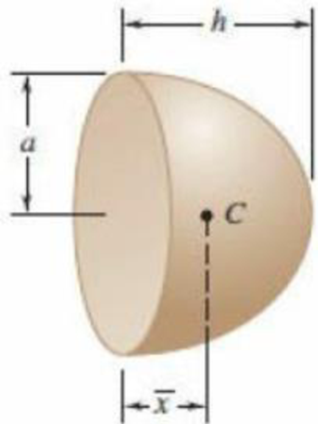
To determine the value of $\overline{x}$ for the two volumes.

Answer to Problem 5.123P

The value of $\overline{x}$ for the first component is $\frac{21}{88}h$, and the value of $\overline{x}$ for the second component is $\frac{27}{40}h$.

Explanation of Solution

Refer Fig. P5.21 and Fig. 1.

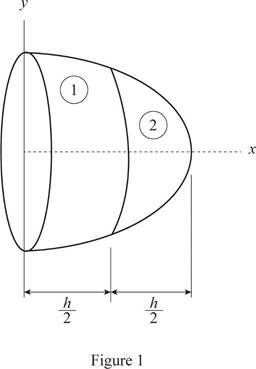
Let the element of volume of the disk be of radius r and thickness dx.

Find the equation for radius from the equation of the generating curve.

$\begin{array}{c}\frac{x^2}{h^2}+\frac{y^2}{a^2}=1\\ r^2=\frac{a^2}{h^2}\left(h^2-x^2\right)\end{array}$

Here, the y component is equal to the radius, $h$ is the radius of the semi ellipsoid, $x$ is the centroid of the element and $dx$ is the thickness of the element.

Write the expression for the volume of the element.

$\begin{array}{c}dV=\pi r^{2}dx\\ =\pi \frac{a^2}{h^2}\left(h^2-x^2\right)dx\end{array}$ (I)

Find the centroid of the element.

$\overline{x_{EL}}=x$

Here, $\overline{x_{EL}}$ is the centroid of the element.

Write the expression for the $\overline{x}$ for the volume.

$\begin{array}{c}\overline{x}V={\displaystyle \underset{}{\int }\overline{x_{EL}}}dV\\ \overline{x}=\frac{{\displaystyle \underset{}{\int }\overline{x_{EL}}}dV}{V}\end{array}$ (II)

Conclusion:

Refer Fig.2

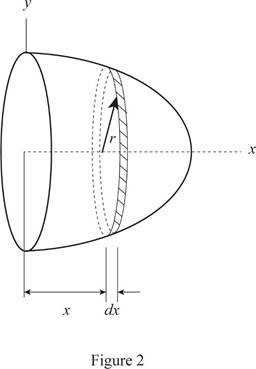
Calculate the volume of component 1.

$\begin{array}{c}{V}_1={\displaystyle {\int }_0^{h/2}dV}\\ ={\displaystyle {\int }_0^{h/2}\pi \frac{a^2}{h^2}\left(h^2-x^2\right)dx}\\ =\pi \left(\frac{a^2}{h^2}\right){\left[h^{2}x-\frac{x^3}{3}\right]}_0^{h/2}\\ =\frac{11}{24}\pi a^{2}h\end{array}$

Calculate ${\displaystyle \underset{1}{\int }\overline{x_{EL}}}dV$ for component 1.

$\begin{array}{c}{\displaystyle \underset{1}{\int }\overline{x_{EL}}}dV={\displaystyle {\int }_0^{h/2}x\left[\pi \frac{a^2}{h^2}\left(h^2-x^2\right)dx\right]}\\ =\pi \left(\frac{a^2}{h^2}\right){\left[h^2\frac{x^2}{2}-\frac{x^4}{4}\right]}_0^{h/2}\\ =\frac{7}{64}\pi a^2{h}^2\end{array}$

Substitute $\frac{7}{64}\pi a^2{h}^2$ for ${\displaystyle \underset{1}{\int }\overline{x_{EL}}}dV$ and $\frac{11}{24}\pi a^{2}h$ for $V_1$ in equation (II).

$\begin{array}{c}\overline{x_1}=\frac{\frac{7}{64}\pi a^2{h}^2}{\frac{11}{24}\pi a^{2}h}\\ =\frac{21}{88}h\end{array}$

Thus, the value of $\overline{x}$ for the first component is $\frac{21}{88}h$.

Calculate the volume of component 2.

$\begin{array}{c}{V}_2={\displaystyle {\int }_{h/2}^{h}dV}\\ ={\displaystyle {\int }_{h/2}^h\pi \frac{a^2}{h^2}\left(h^2-x^2\right)dx}\\ =\pi \left(\frac{a^2}{h^2}\right){\left[h^{2}x-\frac{x^3}{3}\right]}_{h/2}^h\\ =\pi \left(\frac{a^2}{h^2}\right)\left\{\left[h^2\left(h\right)-\frac{h^3}{3}\right]-\left[h^2\left(\frac{h}{2}\right)-\frac{{\left(\frac{h}{2}\right)}^3}{3}\right]\right\}\\ =\frac{5}{24}\pi a^{2}h\end{array}$

Calculate ${\displaystyle \underset{2}{\int }\overline{x_{EL}}}dV$ for component 2.

$\begin{array}{c}{\displaystyle \underset{2}{\int }\overline{x_{EL}}}dV={\displaystyle {\int }_{a/2}^{a}x\left[\pi \frac{a^2}{h^2}\left(h^2-x^2\right)dx\right]}\\ =\pi \left(\frac{a^2}{h^2}\right){\left[h^2\frac{x^2}{2}-\frac{x^4}{4}\right]}_{h/2}^h\\ =\pi \left(\frac{a^2}{h^2}\right)\left\{\left[h^2\frac{h^2}{2}-\frac{h^4}{4}\right]-\left[h^2\frac{{\left(\frac{h}{2}\right)}^2}{2}-\frac{{\left(\frac{h}{2}\right)}^4}{4}\right]\right\}\\ =\frac{9}{64}\pi a^2{h}^2\end{array}$

Substitute $\frac{9}{64}\pi a^2{h}^2$ for ${\displaystyle \underset{2}{\int }\overline{x_{EL}}}dV$ and $\frac{5}{24}\pi a^{2}h$ for $V_2$ in equation (II).

$\begin{array}{c}\overline{x_2}=\frac{\frac{9}{64}\pi a^2{h}^2}{\frac{5}{24}\pi a^{2}h}\\ =\frac{27}{40}h\end{array}$

Thus, the value of $\overline{x}$ for the second component is $\frac{27}{40}h$.

Therefore, the value of $\overline{x}$ for the first component is $\frac{21}{88}h$, and the value of $\overline{x}$ for the second component is $\frac{27}{40}h$.