Mathematical Excursions (MindTap Course List)
4th Edition
ISBN: 9781305965584
Author: Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Clegg
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.4, Problem 1EE
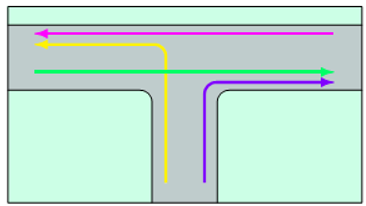
A one-way road ends at a two-way street. The intersection and the different possible traffic routes are shown in the figure below. The one-way road has a left-turn light. Represent the traffic routes with a graph and use graph coloring to determine the minimum number of stages required for a light cycle.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
I need the last answer t=?
I did got the answer for the first two this is just homework.
Saved
Tempo Company's fixed budget (based on sales of 18,000 units) folllows
Fixed Budget
Sales (18,000 units x $201 per unit)
3,618,000
Costs
Direct materials
Direct labor
Indirect materials
Supervisor salary
432,000
792,000
486,000
232,000
Sales commissions
126,000
Shipping
270,000
Administrative salaries
232,000
Depreciation-office equipment
252,000
Insurance
222,000
Office rent
232,000
Income
292,000
1. Compute total variable cost per unit.
2. Compute total fixed costs
3. Prepare a flexible budget at activity levels of 16,000 units and 20,000 units.
Complete this question by entering your answers in the tabs below.
Q Search
hp
PRES
0
O
y=x-9
y= 2x+4
Chapter 5 Solutions
Mathematical Excursions (MindTap Course List)
Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - Explain why the following pen-tracing puzzle is...Ch. 5.1 - Transportation An X in the table below indicates a...Ch. 5.1 - Transportation The table below shows the nonstop...Ch. 5.1 - Social Network A group of friends is represented...Ch. 5.1 - Prob. 4ESCh. 5.1 - Determine (a) the number of edges in the graph,...
Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Explain why the following two graphs cannot be...Ch. 5.1 - Label the vertices of the second graph so that it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Transportation For the train routes given in...Ch. 5.1 - Transportation For the direct air flights given in...Ch. 5.1 - Pets The diagram below shows the arrangement of a...Ch. 5.1 - Transportation A subway map is shown below. Is it...Ch. 5.1 - Prob. 29ESCh. 5.1 - Prob. 30ESCh. 5.1 - Degrees of Separation In the graph below, an edge...Ch. 5.1 - Social Network In the graph below, an edge...Ch. 5.1 - Prob. 33ESCh. 5.1 - Travel A map of South America is shown at the...Ch. 5.2 - Continue investigating Hamiltonian circuits in...Ch. 5.2 - Use the greedy algorithm and the weighted graph...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Transportation For the train routes given in...Ch. 5.2 - Transportation For the direct air flights given in...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Travel A company representative lives in...Ch. 5.2 - Travel A tourist is staying in Toronto, Canada,...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Nicole wants to tour Asia. She will start...Ch. 5.2 - Travel The prices for traveling between five...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Route Planning Brian needs to visit the pet store,...Ch. 5.2 - Route Planning A bike messenger needs to deliver...Ch. 5.2 - Scheduling A research company has a large...Ch. 5.2 - Computer Networks A small office wishes to network...Ch. 5.2 - Route Planning A security officer patrolling a...Ch. 5.2 - Route Planning A city engineer needs to inspect...Ch. 5.2 - Draw a connected graph with six vertices that has...Ch. 5.2 - Assign weights to the edges of the following...Ch. 5.3 - The tetrahedron in figure 5.20 consists of four...Ch. 5.3 - The following graph is the projection of one ofthe...Ch. 5.3 - Prob. 3EECh. 5.3 - Give a reason why the graph below Cannot be the...Ch. 5.3 - Prob. 1ESCh. 5.3 - Prob. 2ESCh. 5.3 - Prob. 3ESCh. 5.3 - Prob. 4ESCh. 5.3 - Prob. 5ESCh. 5.3 - Prob. 6ESCh. 5.3 - Prob. 7ESCh. 5.3 - Prob. 8ESCh. 5.3 - Prob. 9ESCh. 5.3 - Prob. 10ESCh. 5.3 - Prob. 11ESCh. 5.3 - Prob. 12ESCh. 5.3 - Show that the following graph contracts to K5.Ch. 5.3 - Show that the following graph contracts to the...Ch. 5.3 - Prob. 15ESCh. 5.3 - Prob. 16ESCh. 5.3 - Prob. 17ESCh. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Prob. 23ESCh. 5.3 - Prob. 24ESCh. 5.3 - Prob. 25ESCh. 5.3 - Prob. 26ESCh. 5.3 - Prob. 27ESCh. 5.3 - Prob. 28ESCh. 5.3 - Prob. 29ESCh. 5.3 - Prob. 30ESCh. 5.4 - A one-way road ends at a two-way street. The...Ch. 5.4 - A one-way road intersects a two-way road in a...Ch. 5.4 - A two-way road intersects another two-way road in...Ch. 5.4 - Prob. 1ESCh. 5.4 - Prob. 2ESCh. 5.4 - Prob. 3ESCh. 5.4 - Prob. 4ESCh. 5.4 - Prob. 5ESCh. 5.4 - Prob. 6ESCh. 5.4 - Prob. 7ESCh. 5.4 - Prob. 8ESCh. 5.4 - Prob. 9ESCh. 5.4 - Prob. 10ESCh. 5.4 - Prob. 11ESCh. 5.4 - Prob. 12ESCh. 5.4 - Prob. 13ESCh. 5.4 - Prob. 14ESCh. 5.4 - Prob. 15ESCh. 5.4 - Prob. 16ESCh. 5.4 - Prob. 17ESCh. 5.4 - Prob. 18ESCh. 5.4 - Prob. 19ESCh. 5.4 - Prob. 20ESCh. 5.4 - Prob. 21ESCh. 5.4 - Prob. 22ESCh. 5.4 - Scheduling Six different groups of children would...Ch. 5.4 - Scheduling Five different charity organizations...Ch. 5.4 - Scheduling Students in a film class have...Ch. 5.4 - Animal Housing A researcher has discovered six new...Ch. 5.4 - Prob. 27ESCh. 5.4 - Prob. 28ESCh. 5.4 - Prob. 29ESCh. 5.4 - Prob. 30ESCh. 5.4 - Scheduling Edge colorings, as explained in...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - Soccer In the table below, an X indicates teams...Ch. 5 - Each vertex in the graph at the left represents a...Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Architecture The floor plan of a sculpture gallery...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Efficient Route The distances, in miles, between...Ch. 5 - Computer Networking A small office needs to...Ch. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Scheduling A company has scheduled a retreat at a...Ch. 5 - Social Network Each vertex in the graph at the...Ch. 5 - Determine whether the following two graphs are...Ch. 5 - Answer the following questions for the graph shown...Ch. 5 - Recreation The illustration below depicts bridges...Ch. 5 - a. What does Dirac's theorem state? Explain how it...Ch. 5 - Low-Cost Route The table below shows the cost of...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Prob. 8TCh. 5 - Answer the following questions for the graph shown...Ch. 5 - Prob. 10TCh. 5 - Prob. 11TCh. 5 - A group of eight friends is planning a vacation in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 7) 8) Let R be the region bounded by the given curves as shown in the figure. If the line x = k divides R into two regions of equal area, find the value of k 7. y = 3√x, y = √x and x = 4 8. y = -2, y = 3, x = −3, and x = −1 -1 2 +1 R Rarrow_forwardL sin 2x (1+ cos 3x) dx 59arrow_forwardConvert 101101₂ to base 10arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward2) Prove that for all integers n > 1. dn 1 (2n)! 1 = dxn 1 - Ꮖ 4 n! (1-x)+/arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward3) Let a1, a2, and a3 be arbitrary real numbers, and define an = 3an 13an-2 + An−3 for all integers n ≥ 4. Prove that an = 1 - - - - - 1 - - (n − 1)(n − 2)a3 − (n − 1)(n − 3)a2 + = (n − 2)(n − 3)aı for all integers n > 1.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- Definition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward1) If f(x) = g¹ (g(x) + a) for some real number a and invertible function g, show that f(x) = (fo fo... 0 f)(x) = g¯¹ (g(x) +na) n times for all integers n ≥ 1.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY