
Concept explainers
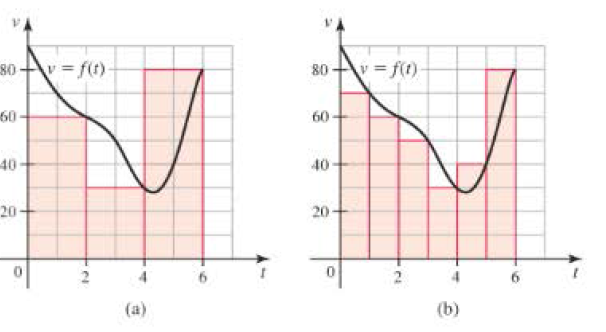
The velocity in ft/s of an object moving along a line is given by v – f(t) on the interval 0 < t < 6 (see figure), where t is measured in seconds.
a. Divide the interval [0, 6] into n = 3 subintervals [0, 2], [2, 4] and [4, 6]. On each subinterval, assume the object moves at a constant velocity equal to the value of v evaluated at the right endpoint of the subinterval, and use these approximations to estimate the displacement of the object on [0, 6] (see part (a) of the figure).
b. Repeat part (a) n = 6 subintervals (see part (b) of the figure).
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Calculus: Early Transcendentals and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition) (Briggs, Cochran, Gillett & Schulz, Calculus Series)
Additional Math Textbook Solutions
Intro Stats, Books a la Carte Edition (5th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Thinking Mathematically (6th Edition)
Pre-Algebra Student Edition
- (4) (8 points) (a) (2 points) Write down a normal vector n for the plane P given by the equation x+2y+z+4=0. (b) (4 points) Find two vectors v, w in the plane P that are not parallel. (c) (2 points) Using your answers to part (b), write down a parametrization r: R² — R3 of the plane P.arrow_forward(2) (8 points) Determine normal vectors for the planes given by the equations x-y+2z = 3 and 2x + z = 3. Then determine a parametrization of the intersection line of the two planes.arrow_forward(3) (6 points) (a) (4 points) Find all vectors u in the yz-plane that have magnitude [u also are at a 45° angle with the vector j = (0, 1,0). = 1 and (b) (2 points) Using the vector u from part (a) that is counterclockwise to j, find an equation of the plane through (0,0,0) that has u as its normal.arrow_forward
- (1) (4 points) Give a parametrization c: R R³ of the line through the points P = (1,0,-1) and Q = (-2, 0, 1).arrow_forward4. Consider the initial value problem y' = 3x(y-1) 1/3, y(xo) = yo. (a) For what points (co, yo) does the IVP have a solution? (b) For what points (xo, yo) does the IVP have a unique solution on some open interval that contains 20? (c) Solve the IVP y' = 3x(y-1) 1/3, y(0) = 9 and determine the largest open interval on which this solution is unique.arrow_forwardFind the limit. (If the limit is infinite, enter 'oo' or '-o', as appropriate. If the limit does not otherwise exist, enter DNE.) lim X→ ∞ (✓ 81x2 - 81x + x 9x)arrow_forward
- 2) Compute the following anti-derivative. √1x4 dxarrow_forwardQuestion 3 (5pt): A chemical reaction. In an elementary chemical reaction, single molecules of two reactants A and B form a molecule of the product C : ABC. The law of mass action states that the rate of reaction is proportional to the product of the concentrations of A and B: d[C] dt = k[A][B] (where k is a constant positive number). Thus, if the initial concentrations are [A] = = a moles/L and [B] = b moles/L we write x = [C], then we have (E): dx dt = k(ax)(b-x) 1 (a) Write the differential equation (E) with separate variables, i.e. of the form f(x)dx = g(t)dt. (b) Assume first that a b. Show that 1 1 1 1 = (a - x) (b - x) - a) a - x b - x b) (c) Find an antiderivative for the function f(x) = (a-x) (b-x) using the previous question. (d) Solve the differentiel equation (E), i.e. find x as a function of t. Use the fact that the initial concentration of C is 0. (e) Now assume that a = b. Find x(t) assuming that a = b. How does this expression for x(t) simplify if it is known that [C] =…arrow_forward3) Find the volume of the solid that lies inside both the sphere x² + y² + z² cylinder x²+y² = 1. = 4 and thearrow_forward
- 1) Compute the following limit. lim x-0 2 cos(x) 2x² - x4arrow_forwardy = f(x) b C The graph of y = f(x) is shown in the figure above. On which of the following intervals are dy > 0 and dx d²y dx2 <0? I. aarrow_forward3 2 1 y O a The graph of the function f is shown in the figure above. Which of the following statements about f is true? о limb f(x) = 2 Olima f(x) = 2 о lima f (x) = lim x →b f(x) → f (x) = 1 limb. lima f(x) does not existarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





