
Concept explainers
Consider the three connected objects shown in Figure P5.88. Assume first that the inclined plane is friction-less and that the system is in equilibrium. In terms of m, g, and θ, find (a) the mass M and (b) the tensions T, and T2. Now assume that the value of Af is double the value found in part (a). Find (c) the acceleration of each object and (d) the tensions T1 and T2. Next, assume that the coefficient of static friction between m and 2m and the inclined plane is m, and that the system is in equilibrium. Find (e) the maximum value of M and (0 the minimum value of M. (g) Compare the values of T2 when M has its minimum and maximum values.
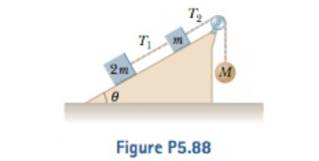
(a)
The expression for the mass of
Answer to Problem 5.88AP
The expression for the mass
Explanation of Solution
The free body diagram of the three connected objects is shown in Figure below,
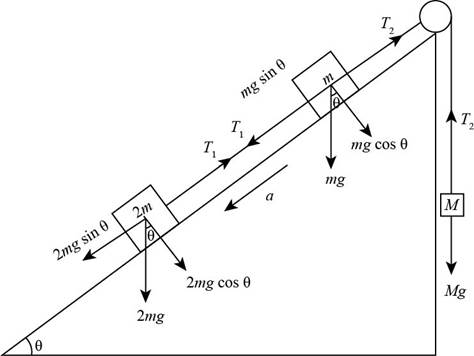
Figure (1)
From Figure (1), the equilibrium forces acts on the object of mass
Here,
From the Newton’s second law of motion, the net force on the object of mass
Here,
Substitute
From Figure (1), the equilibrium forces act on the object of mass
Here,
From the Newton’s second law of motion, the net force on the object of mass
Substitute
Add the equation (1) with equation (2).
From Figure (1), the equilibrium forces act on the object of mass
Here,
Substitute
From the Newton’s second law of motion, the net force on the object of mass
Substitute
The system is in equilibrium so value of the acceleration is zero.
Substitute
Conclusion:
Therefore, the expression for the mass
(b)
The expressions for tensions
Answer to Problem 5.88AP
The expression for the tension
Explanation of Solution
From part (a), the expression for the mass of
From part (a), the equilibrium forces act on the object is,
The system is in equilibrium, the value of acceleration is zero so the net force acts on the system is also zero.
Substitute
Substitute
Thus, the expression for the tension
From part (a), the equation (2) is,
Substitute
Substitute
Thus, the expression for the tension
Conclusion:
Therefore, the expression for the tension
(c)
The acceleration of each object.
Answer to Problem 5.88AP
The acceleration of each object is
Explanation of Solution
Given info: The value of mass
From part (a), the expression for the mass when it is double represents as,
From part (a), the equation (1) is,
Rearrange the above equation.
From part (a), the equation (2) is,
Rearrange the above equation.
Substitute
From Figure (1), the equilibrium forces act on the object of mass
Substitute
Subtract the equation (3) from equation (4).
Conclusion:
Therefore, the acceleration of each object is
(d)
The expressions for tensions
Answer to Problem 5.88AP
The expression for the tension
Explanation of Solution
From part (c), the expression for the acceleration is,
From part (c), the equation for tension
Substitute
Thus, the expression for tension
From part (c), the equation (3) is,
Substitute
Thus, the expression for tension
Conclusion:
Therefore, the expression for the tension
(e)
The maximum value of
Answer to Problem 5.88AP
The maximum value of
Explanation of Solution
Given info: The coefficient of static friction between mass
The static friction forces on the masses
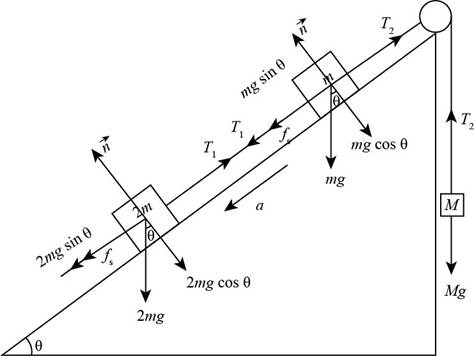
Figure (2)
From the Figure (2), the normal force on the object of mass
The expression for the static friction force on the object of mass
Here,
Substitute
From the Figure (1), the equilibrium forces acts on the object of mass
Substitute
Rearrange the above equation for
Substitute
From the Figure (2), the normal force on the object of mass
Substitute
From the Figure (1), the equilibrium forces acts on the object of mass
Substitute
Add equation (4) with the above equation.
Substitute
The equilibrium forces on the block of mass
Substitute
Conclusion:
Therefore, the maximum value of
(f)
The minimum value of
Answer to Problem 5.88AP
The minimum value of
Explanation of Solution
From part (e), the expression of tension
The equilibrium forces acts on block for minimum mass of
Substitute
Conclusion:
Therefore, the minimum value of
(g)
The difference between the tension
Answer to Problem 5.88AP
The difference between the tension for maximum and minimum mass is
Explanation of Solution
From part (e), the expression for maximum mass is,
From part (f), the expression for the minimum mass is,
From part (e), the expression for the tension for maximum mass is,
From part (f), the expression for the tension for maximum mass is,
Compare both the above equation.
Substitute
Conclusion:
Therefore, the difference between the tension for maximum and minimum mass is
Want to see more full solutions like this?
Chapter 5 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- No chatgpt pls will upvotearrow_forwardNo chatgpt pls will upvote instantarrow_forwardKirchoff's Laws. A circuit contains 3 known resistors, 2 known batteries, and 3 unknown currents as shown. Assume the current flows through the circuit as shown (this is our initial guess, the actual currents may be reverse). Use the sign convention that a potential drop is negative and a potential gain is positive. E₂ = 8V R₁₁ = 50 R₂ = 80 b с w 11 www 12 13 E₁ = 6V R3 = 20 a) Apply Kirchoff's Loop Rule around loop abefa in the clockwise direction starting at point a. (2 pt). b) Apply Kirchoff's Loop Rule around loop bcdeb in the clockwise direction starting at point b. (2 pt). c) Apply Kirchoff's Junction Rule at junction b (1 pt). d) Solve the above 3 equations for the unknown currents I1, 12, and 13 and specify the direction of the current around each loop. (5 pts) I1 = A 12 = A 13 = A Direction of current around loop abef Direction of current around loop bcde (CW or CCW) (CW or CCW)arrow_forward
- No chatgpt pls will upvotearrow_forward4.) The diagram shows the electric field lines of a positively charged conducting sphere of radius R and charge Q. A B Points A and B are located on the same field line. A proton is placed at A and released from rest. The magnitude of the work done by the electric field in moving the proton from A to B is 1.7×10-16 J. Point A is at a distance of 5.0×10-2m from the centre of the sphere. Point B is at a distance of 1.0×10-1 m from the centre of the sphere. (a) Explain why the electric potential decreases from A to B. [2] (b) Draw, on the axes, the variation of electric potential V with distance r from the centre of the sphere. R [2] (c(i)) Calculate the electric potential difference between points A and B. [1] (c(ii)) Determine the charge Q of the sphere. [2] (d) The concept of potential is also used in the context of gravitational fields. Suggest why scientists developed a common terminology to describe different types of fields. [1]arrow_forward3.) The graph shows how current I varies with potential difference V across a component X. 904 80- 70- 60- 50- I/MA 40- 30- 20- 10- 0+ 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 VIV Component X and a cell of negligible internal resistance are placed in a circuit. A variable resistor R is connected in series with component X. The ammeter reads 20mA. 4.0V 4.0V Component X and the cell are now placed in a potential divider circuit. (a) Outline why component X is considered non-ohmic. [1] (b(i)) Determine the resistance of the variable resistor. [3] (b(ii)) Calculate the power dissipated in the circuit. [1] (c(i)) State the range of current that the ammeter can measure as the slider S of the potential divider is moved from Q to P. [1] (c(ii)) Describe, by reference to your answer for (c)(i), the advantage of the potential divider arrangement over the arrangement in (b).arrow_forward
- 1.) Two long parallel current-carrying wires P and Q are separated by 0.10 m. The current in wire P is 5.0 A. The magnetic force on a length of 0.50 m of wire P due to the current in wire Q is 2.0 × 10-s N. (a) State and explain the magnitude of the force on a length of 0.50 m of wire Q due to the current in P. [2] (b) Calculate the current in wire Q. [2] (c) Another current-carrying wire R is placed parallel to wires P and Q and halfway between them as shown. wire P wire R wire Q 0.05 m 0.05 m The net magnetic force on wire Q is now zero. (c.i) State the direction of the current in R, relative to the current in P.[1] (c.ii) Deduce the current in R. [2]arrow_forward2.) A 50.0 resistor is connected to a cell of emf 3.00 V. The voltmeter and the ammeter in the circuit are ideal. V A 50.00 (a) The current in the ammeter is 59.0 mA. Calculate the internal resistance of the cell. The circuit is changed by connecting another resistor R in parallel to the 50.0 resistor. V A 50.00 R (b) Explain the effect of this change on R is made of a resistive wire of uniform cross-sectional area 3.1 × 10-8 m², resistivity 4.9 × 10-70m and length L. The resistance of R is given by the equation R = KL where k is a constant. (b.i) the reading of the ammeter. [2] (b.ii) the reading of the voltmeter. [2] (c) Calculate k. State an appropriate unit for your answer. [3] [2]arrow_forwardNo chatgpt pls will upvotearrow_forward
- No chatgpt pls will upvotearrow_forwardA rod 12.0 cm long is uniformly charged and has a total charge of -20.0 μc. Determine the magnitude and direction of the electric field along the axis of the rod at a point 32.0 cm from its center. 361000 ☑ magnitude What is the general expression for the electric field along the axis of a uniform rod? N/C direction toward the rodarrow_forwardA certain brand of freezer is advertised to use 730 kW h of energy per year. Part A Assuming the freezer operates for 5 hours each day, how much power does it require while operating? Express your answer in watts. ΜΕ ΑΣΦ ? P Submit Request Answer Part B W If the freezer keeps its interior at a temperature of -6.0° C in a 20.0° C room, what is its theoretical maximum performance coefficient? Enter your answer numerically. K = ΜΕ ΑΣΦ Submit Request Answer Part C What is the theoretical maximum amount of ice this freezer could make in an hour, starting with water at 20.0°C? Express your answer in kilograms. m = Ο ΑΣΦ kgarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





