Chapter 5, Problem 5.53P

5.53.20 Chemicals are stored in a laboratory with volume V(m³). As a consequence of poor laboratory practices, a hazardous species, A, enters the room air (from inside the room) at a constant rate 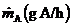The room is ventilated with clean air ?owing at a constant rate 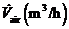The average concentration of A in the room air builds up until it reaches a steady-state value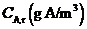

(a) List at least four situations that could lead to A getting into the room air.

(b) Assume that the A is perfectly mixed with the room air and derive the formula

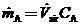
(c) The assumption of perfect mixing is never justi?ed when the enclosed space is a room (as opposed to, say, a stirred reactor). In practice, the concentration of A varies from one point in the room to another: it is relatively high near the point where A enters the room air and relatively low in regions far from that point, including the ventilator outlet duct. If we say that 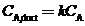where 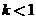is a nonideal mixing factor (generally between 0.1 and 0.5, with the lowest value corresponding to the poorest mixing). then the equation of Part (b) becomes

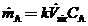
Use this equation and the ideal-gas equation of state to derive the following expression for the average mole fraction of A in the room air:

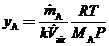
where M_A is the molecular weight of A.

(b) The permissible exposure level (PEL) for styrene (M = 104.14) de?ned by the U.S. Occupational Safety and Health Administration is 50 ppm (molar basis).21 An open storage tank in a polymerization laboratory contains styrene. The evaporation rate from this tank is estimated to be 9.0 g/h. Room temperature is 20°C. Assuming that the laboratory air is reasonably well mixed (so that k = 0.5), calculate the minimum ventilation rate (m³/h) required to keep the average styrene concentration at or below the PEL. Then give several reasons why working in the laboratory might still be hazardous if the calculated minimum ventilation rate is used.

(e) Would the hazard level in the situation described in Part (d) increase or decrease if the temperature in the room were to increase? (Increase, decrease, no way to tell.) Explain your answer, citing at least two effects of temperature in your explanation.