
(a)
The distance
Answer to Problem 5.2.2P
Explanation of Solution
Given:
An unsymmetrical flexural member consists of a
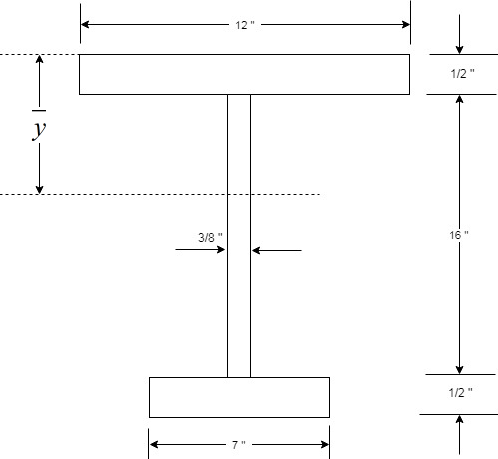
Concept Used:
As the given flexural member is unsymmetrical, therefore, the plastic neutral axis of the section won’t lie on the center of the member.
We will use the concept of equilibrium of forces, to calculate the distance
Calculation:
Now, as we have the following equation
Where,
As the force is equal, we have
Now, calculating the area of the top flange, as follows:
Substituting the values, we have
Calculating the area of the web above the neutral axis, as follows:
Substituting the values, we have
Now, calculating the area of component above the plastic neutral axis as follows:
Now, calculating the area of the bottom flange, we have
Substitute the
Calculating the area of the web below the neutral axis, as follows:
Substituting the values, we have
Calculating the area of the component below the plastic neutral axis as follows:
Now for computing the neutral axis, use
Substitute the values, we have
Conclusion:
Therefore, the distance
(b)
Plastic moment MPfor the horizontal plastic neutral axis.
Answer to Problem 5.2.2P
Explanation of Solution
Given:
An unsymmetrical flexural member consists of a
Calculation:
We have the following formula for the plastic moment of the section
Where,
And we have following formula for calculating the plastic section modulus
We have,
As we have calculated, the distance
We now have the following diagram to consider:
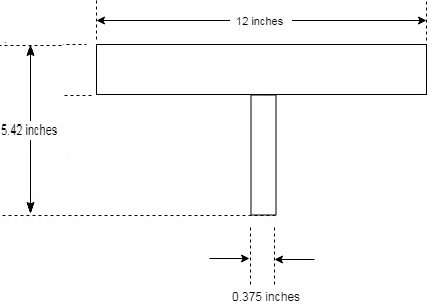
Calculate the area of the top flange as follows:
Now, the area of the web portion that is left is as follows:
Now, calculating the centroidal distance of the web as follows:
Now, calculating the centroidal distance of the top flange as follows:
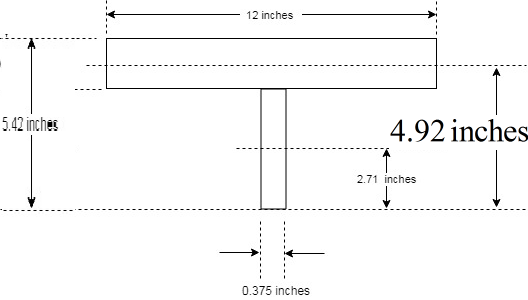
Following figure shows the centroidal distances that were found in the above steps.
Calculating
| Member Component | |||
| Web | |||
| Top Flange | |||
| Total |
Now calculating the value of
Now, similarly find for the lower half section, we have the following figure
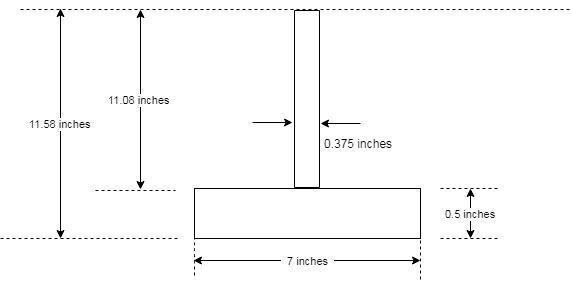
Calculate the area of the bottom flange as follows:
Now, the area of the web portion that is left is as follows:
Now, calculating the centroidal distance of the web as follows:
Now, calculating the centroidal distance of the bottom flange as follows:
Calculating
| Member Component | |||
| Web | |||
| Top Flange | |||
| Total |
Now calculating the value of
Now, calculating the plastic section modulus as follows:
Substituting the values, we have
And
Now, for the plastic moment of the section, we have
Substituting the values
Conclusion:
Therefore, the plastic moment MP for the horizontal plastic neutral axis is
(c)
The plastic section modulus Z with respect to the minor principal axis.
Answer to Problem 5.2.2P
Explanation of Solution
Given:
An unsymmetrical flexural member consists of a
Calculation:
To find thePlastic section modulus Z with respect to the minor principal axis, we need to know that the vertical line or axis is considered to be the minor principal axis, therefore as we know that the member is symmetrical along the y-axis, and the same axis is the minor principal axis which confirms that the plastic neutral axis is passing through its center.
We have the following formula for the plastic section modulus:
Where,
and A is the total area of cross section.
Now, as we know that the plastic neutral axis is passing through the center of the minor principal axis, we conclude
And know we need to find any one of them and let that be equal to
Thus, we have
We can find the
| Member Component | |||
| Top Flange | |||
| Web | |||
| Bottom Flange | |||
| Total |
Calculating the centroidal distance as follows:
Calculation of plastic section modulus is as follows:
Substituting the values, we have
Conclusion:
Therefore, the value of plastic section modulus Z with respect to the minor principal axis is
Want to see more full solutions like this?
Chapter 5 Solutions
STEEL DESIGN W/ ACCESS
- nent 6-Transverse Shear & Deflection ↓ 2 of 2 -+ Automatic Zoom 4.) The built-up wooden beam shown is subjected to a vertical shear of 8 kN. Knowing the the nails are spaced longitudinally every 60 mm at A and every 25 mm at B, determine the shear force in the nails at A and B. (5 points) 50 300- 400 A 50 A C 150 B A 100 50 200 A B Dimensions in mm 5.) A 2.5 inch x 5.5 inch rectangular Southern pine section (E=1.8 x 103 ksi) is used in an 8 ft cantilever span subjected to the loads shown. Compute the deflections at point A. (4 points) Дarrow_forwardE:/school%20pack/BENG%202/EG231/STATICS/LECTURE%20NOTES/PRACTICE%20QUESTIONS/EG%20231%20Chap-5%20Practice%20Que PDF 豆豆豆豆豆豆 aw V Aa | Ask Copilot - + 4 of 8 D 3. Calculate the y-coordinate of the centroid of the shaded area. 74 mm y 3232 mm mm DELL 32 mm -x F1 F2 F3 F4 F5 F6 F7 F8 F9 prt sc F10 home end F11 F 2 W E3 $ 4 € 95 % & 6 7 8 * 00 R T Y כ 9 O Parrow_forward*8-60. The 2-in.-diameter rod is subjected to the forces shown. Determine the state of stress at point B, and show the results on a differential element located at this point. Probs. 8-59/60 B 8 in. 600 lb 12 in. 500 lb 800 lbarrow_forward
- find SFD and BMD by using slope deflection methodarrow_forwardThe following relates to Problems 4 and 5. Christchurch, New Zealand experienced a major earthquake on February 22, 2011. It destroyed 100,000 homes. Data were collected on a sample of 300 damaged homes. These data are saved in the file called CIEG315 Homework 4 data.xlsx, which is available on Canvas under Files. A subset of the data is shown in the accompanying table. Two of the variables are qualitative in nature: Wall construction and roof construction. Two of the variables are quantitative: (1) Peak ground acceleration (PGA), a measure of the intensity of ground shaking that the home experienced in the earthquake (in units of acceleration of gravity, g); (2) Damage, which indicates the amount of damage experienced in the earthquake in New Zealand dollars; and (3) Building value, the pre-earthquake value of the home in New Zealand dollars. PGA (g) Damage (NZ$) Building Value (NZ$) Wall Construction Roof Construction Property ID 1 0.645 2 0.101 141,416 2,826 253,000 B 305,000 B T 3…arrow_forwardfind SFD and BMDarrow_forward
- The data needed to answer this question is given by this link: https://docs.google.com/spreadsheets/d/1vzb03U7Uvzm7X-by3OchQNwYeREzbP6Z-xzZMP2tzNw/edit?usp=sharing if it is easier to make a copy of the data because it is on view only then feel free to do so.arrow_forwardThe data needed to answer this question is given in the following link (file is on view only so if you would like to make a copy to make it easier for yourself feel free to do so) https://docs.google.com/spreadsheets/d/1aV5rsxdNjHnkeTkm5VqHzBXZgW-Ptbs3vqwk0SYiQPo/edit?usp=sharingarrow_forwardA k 000 6 ft A kips Bl D ft C C kips 10 ft 12 ft E B k/ft D E ft tarrow_forward
- H.W: show that the equations 1. (x+y)dy+(x-y)dx = 0 2. x²dy+(y²-xy)dx = 0 are homogeneous and solve:arrow_forwardH.W: Solve the differential equation y' - (1+x)(1 + y²) = 0arrow_forwardThe benchmark is 00.00. The backsights are 6.00, 9.32 and 13.75 and 14.00 The foresights are 6.00, 9.00 and 3.22. What is the height of the instrument? H.I. - 100.00 - 124.85 - 43.07- 24.85arrow_forward
 Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning

