Chapter 5, Problem 1P

Determine the real roots of $f\left(x\right)=-0.5x^2+2.5x+4.5$:

(a) Graphically.

(b) Using the quadratic formula.

(c) Using three iterations of the bisection method to determine the highest root. Employ initial guesses of $x_l=5{\text{ and x}}_u=10$.

Compute the estimated error ${\epsilon }_a$ and the true error ${\epsilon }_t$ after each iteration.

To determine

The real roots of the equation $f\left(x\right)=-0.5x^2+2.5x+4.5$ using the graphical method.

Answer to Problem 1P

Solution:

The real roots of the equation are $-1.4$ and 6.4.

Explanation of Solution

Given Information:

The equation $f\left(x\right)=-0.5x^2+2.5x+4.5$.

Calculation:

The graph of the function can be plotted using MATLAB.

Code:

clc;

x=linspace(-2,8);

y1=-0.5*x.^2+2.5*x+4.5;

y2=0;

plot(x,y1);

hold on

line([-2,8],[y2,y2])

Output:

This gives the following plot:

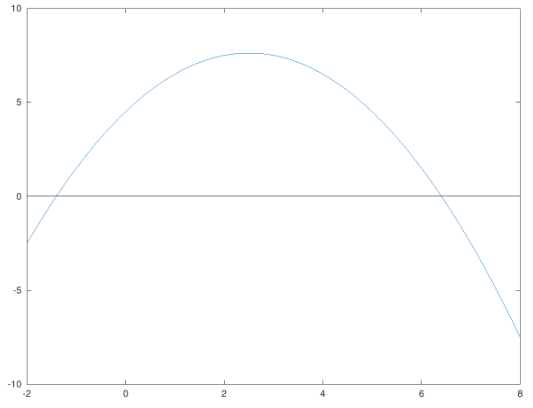
The roots of an equation can be represented graphically by the x-coordinate of the point where the graph cuts the x-axis. From the plot, the two zeros of the equation can be approximated as $-1.4$ and 6.4.

To determine

To calculate: The real roots of the equation $f\left(x\right)=-0.5x^2+2.5x+4.5$ using the quadratic formula.

Answer to Problem 1P

Solution:

The roots of the equation are $-1.40512484$ and $6.40512484$.

Explanation of Solution

Given Information:

The equation $f\left(x\right)=-0.5x^2+2.5x+4.5$.

Formula Used:

The roots of an equation $a{x}^2+bx+c$ can be obtained using the quadratic formula as:

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Calculation:

Consider the provided equation,

$f\left(x\right)=-0.5x^2+2.5x+4.5$

Now substitute $-0.5$ for a, 2.5 for b and 4.5 for c in the quadratic formula to get the roots as:

$\begin{array}{c}x=\frac{-2.5\pm \sqrt{{2.5}^2-4\left(-0.5\right)\left(4.5\right)}}{2\left(-0.5\right)}\\ =\frac{-2.5\pm 3.90512484}{-1}\\ =-1.40512484,6.40512484\end{array}$

Thus, the roots of the equation are $-1.40512484$ and $6.40512484$.

To determine

To calculate: The highest root of the equation $f\left(x\right)=-0.5x^2+2.5x+4.5$ using three iterations of the bisection method by assuming $x_l$ and $x_u$ to be 5 and 10 respectively while computing the true and estimated errors after each iteration.

Answer to Problem 1P

Solution:

The highest root of the equation can be approximated as 6.875. The true and approximate errors are as follows:

$\begin{array}{ccc}n& {\epsilon }_a& {\epsilon }_t\\ 1& -& 17.1\%\\ 2& 20\%& 2.42\%\\ 3& 9.09\%& 7.32\%\end{array}$

Explanation of Solution

Given Information:

The equation $f\left(x\right)=-0.5x^2+2.5x+4.5$.

Formula Used:

A root of an equation can be obtained using the bisection method as follows:

1. Choose 2 values x, say a and b such that $f\left(a\right)f\left(b\right)<0$.

2. Now, estimate the root by $x_1=\frac{a+b}{2}$.

3. If, $f\left(a\right)f\left(x_1\right)<0$, the root would lie between a and $x_1$. Now assume the next root to be $x_2=\frac{a+x_1}{2}$. If, $f\left(a\right)f\left(x_1\right)>0$, the root would lie between b and $x_1$. Now assume the next root to be $x_2=\frac{b+x_1}{2}$ and if $f\left(a\right)f\left(x_1\right)=0$, the root is $x_1$.

Calculation:

For the provided function:

$\begin{array}{c}f\left(5\right)=-0.5{\left(5\right)}^2+2.5\left(5\right)+4.5\\ =4.5\\ f\left(10\right)=-0.5{\left(10\right)}^2+2.5\left(10\right)+4.5\\ =-20.5\end{array}$

Hence,

$f\left(5\right)f\left(10\right)<0$

Now take the first root to be,

$\begin{array}{c}{x}_1=\frac{5+10}{2}\\ =7.5\end{array}$

As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:

$\begin{array}{c}{\epsilon }_t=\left(\left|\frac{6.40512484-7.5}{6.40512484}\right|\times 100\right)\%\\ =17.1\%\end{array}$

The true error is 17.1%. There would be no approximate error for the first iteration.

Now,

$\begin{array}{c}f\left(7.5\right)=-0.5{\left(7.5\right)}^2+2.5\left(7.5\right)+4.5\\ =-4.875\end{array}$

Thus, $f\left(5\right)f\left(7.5\right)<0$. This implies that the root would be between 5 and 7.5.

Now, the second root would be:

$\begin{array}{c}{x}_2=\frac{5+7.5}{2}\\ =6.25\end{array}$

As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:

$\begin{array}{c}{\epsilon }_t=\left(\left|\frac{6.40512484-6.25}{6.40512484}\right|\times 100\right)\%\\ =2.42\%\end{array}$

The true error is 2.42%.

The approximate error can be computed as:

$\begin{array}{c}{\epsilon }_a=\left(\left|\frac{6.25-7.5}{6.25}\right|\times 100\right)\%\\ =20\%\end{array}$

The approximate error is 2%.

Now,

$\begin{array}{c}f\left(6.5\right)=-0.5{\left(6.5\right)}^2+2.5\left(6.5\right)+4.5\\ =0.59375\end{array}$

Thus, $f\left(5\right)f\left(6.25\right)>0$. This implies that the root would be between 6.25 and 7.5.

Now, the third root would be:

$\begin{array}{c}{x}_3=\frac{6.25+7.5}{2}\\ =6.875\end{array}$

As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:

$\begin{array}{c}{\epsilon }_t=\left(\left|\frac{6.40512484-6.875}{6.40512484}\right|\times 100\right)\%\\ =7.34\%\end{array}$

The true error is 7.34%.

The approximate error can be computed as:

$\begin{array}{c}{\epsilon }_a=\left(\left|\frac{6.875-6.25}{6.875}\right|\times 100\right)\%\\ =9.09\%\end{array}$

The approximate error is 9.09%.

Thus, the highest root can be approximated as 6.875.