Chapter 4.P4, Problem 4P

Problems $4$ and $5$ are concerned with systems that have two degrees of freedom. The generalization of Eq. $\left(1\right)$ to a functional with two degrees of freedom is

$J\left(x,y\right)={\displaystyle \underset{a}{\overset{b}{\int }}F\left(t,x,\text{}y,x^{\prime },y^{\prime }\right)dt}$, $\left(7\right)$

where $t$ is a parameter, not necessarily time. Necessary conditions, stated as differential equations, for a vector-valued function $t\to \langle \bar{x}\left(t\right),\bar{y}\left(t\right)\rangle$ to be a stationary function of Eq. $\left(7\right)$ are found by an analysis that is analogous to that leading up to Eq. $\left(6\right)$. Consider the perturbed functional

$\varphi \left(\epsilon \right)=J\left(\bar{x}+\epsilon \xi ,\bar{y}+\epsilon \eta \right)$

$={\displaystyle \underset{a}{\overset{b}{\int }}F\left(t,\bar{x}+\epsilon \xi ,\bar{y}+\epsilon {\eta }^{\prime },{\bar{x}}^{\prime }+\epsilon \xi ,{\bar{y}}^{\prime }+\epsilon {\eta }^{\prime }\right)dt}$, $\left(8\right)$

where the perturbation vector $\langle \xi \left(t\right),\eta \left(t\right)\rangle$ satisfies

$\langle \xi \left(a\right),\eta \left(a\right)\rangle =\langle 0,0\rangle$ and $\langle \xi \left(b\right),\eta \left(b\right)\rangle =\langle 0,0\rangle$. $\left(9\right)$

Thus, for $\varphi \left(\epsilon \right)$ defined by Eq. $\left(8\right)$, we compute $\varphi \left(0\right)=0$, integrate by parts, and use the endpoint conditions $\left(9\right)$ to arrive at

${\displaystyle \underset{a}{\overset{b}{\int }}\left\{\left[F_x-F_{x^{\prime }t}\right]\xi +\left[F_y-F_{y^{\prime }t}\right]\eta \right\}dt=0}$. $\left(10\right)$

Since Eq. $\left(10\right)$ must hold for any $\xi$ and $\eta$ satisfying the conditions $\left(9\right)$, we conclude that each factor multiplying $\xi$ and $\eta$ in the integrand must equal zero,

$\begin{array}{l}{F}_x-F_{x^{\prime }t}=0\\ F_y-F_{y^{\prime }t}=0\end{array}$. $\left(11\right)$

Thus the Euler-Lagrange equations for the function $\left(7\right)$ are given by the system $\left(11\right)$.

$J\left(y\right)={\displaystyle \underset{a}{\overset{b}{\int }}F\left(x,y,y^{\prime }\right)dx}$, $\left(1\right)$

$\frac{\partial F}{\partial y}\left(x,y,y^{\prime }\right)-\frac{{\partial }^{2}F}{\partial x\partial y^{\prime }}\left(x,y,y^{\prime }\right)=0.$ $\left(6\right)$

A Two-Mass, Three-Spring System. Consider the mechanical system consisting of two masses and three springs shown in Figure $\text{4}\text{.P}\text{.7}$.

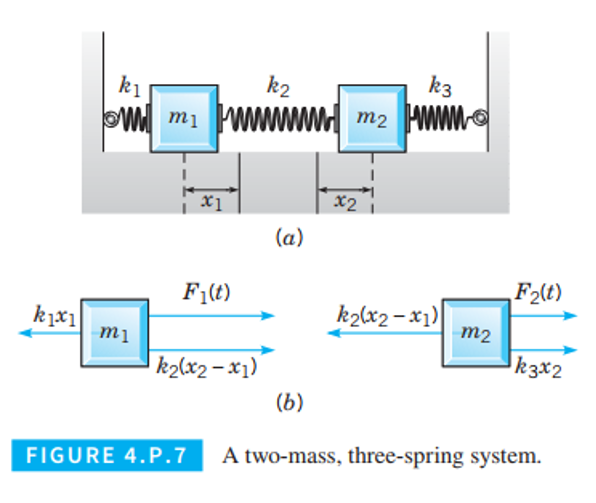
Find the action integral for this system and the Euler-Lagrange equations for the positions $x_1\left(t\right)$ and $x_2\left(t\right)$ of the two masses.