14th Edition

ISBN: 9781323907733

Author: Barnett

Publisher: INTER PEAR

See similar textbooks

Videos

Textbook Question

Chapter 4.6, Problem 66E

Construct a mathematical model for each of the following problems. (The answers in the back of the book include both the mathematical model and the interpretation of its solution.) Use matrix

inverse methods to solve the model and then interpret the solution.

Production scheduling. Labor and material costs for manufacturing two guitar models are given in the table:

Chapter 4.6, Problem 66E, Construct a mathematical model for each of the following problems. (The answers in the back of the , example 1

(A) If a total of $ 3 , 000 a week is allowed for labor and material, how many of each model should be produced each week to use exactly each of the allocations of the $ 3 , 000 indicated in the following table?

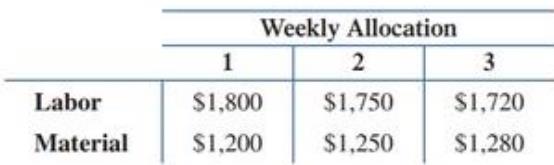
Chapter 4.6, Problem 66E, Construct a mathematical model for each of the following problems. (The answers in the back of the , example 2

(B) Is it possible to use an allocation of $ 1 , 600 for labor and $ 1 , 400 for material? Of $ 2 , 000 for labor and $ 1 , 000 for material? Explain.

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 4.6, Problem 65E

Chapter 4.6, Problem 67E

Students have asked these similar questions

5. (a) State the Residue Theorem. Your answer should include all the conditions required for the theorem to hold. (4 marks) (b) Let y be the square contour with vertices at -3, -3i, 3 and 3i, described in the anti-clockwise direction. Evaluate に dz. You must check all of the conditions of any results that you use. (5 marks) (c) Evaluate L You must check all of the conditions of any results that you use. ཙ x sin(Tx) x²+2x+5 da. (11 marks)

3. (a) Lety: [a, b] C be a contour. Let L(y) denote the length of y. Give a formula for L(y). (1 mark) (b) Let UCC be open. Let f: U→C be continuous. Let y: [a,b] → U be a contour. Suppose there exists a finite real number M such that |f(z)| < M for all z in the image of y. Prove that < ||, f(z)dz| ≤ ML(y). (3 marks) (c) State and prove Liouville's theorem. You may use Cauchy's integral formula without proof. (d) Let R0. Let w € C. Let (10 marks) U = { z Є C : | z − w| < R} . Let f UC be a holomorphic function such that 0 < |ƒ(w)| < |f(z)| for all z Є U. Show, using the local maximum modulus principle, that f is constant. (6 marks)

3. (a) Let A be an algebra. Define the notion of an A-module M. When is a module M a simple module? (b) State and prove Schur's Lemma for simple modules. (c) Let AM(K) and M = K" the natural A-module. (i) Show that M is a simple K-module. (ii) Prove that if ƒ € Endд(M) then ƒ can be written as f(m) = am, where a is a matrix in the centre of M, (K). [Recall that the centre, Z(M,(K)) == {a Mn(K) | ab M,,(K)}.] = ba for all bЄ (iii) Explain briefly why this means End₁(M) K, assuming that Z(M,,(K))~ K as K-algebras. Is this consistent with Schur's lemma?

Chapter 4 Solutions

FINITE MATHMATICS F/ BUSI...-ACCESS

Ch. 4.1 - Can a consistent and dependent system have exactly...Ch. 4.1 - Return to Example 2 and solve each system by...Ch. 4.1 - Solve by graphing and check: 2xy=3x+2y=4 Ch. 4.1 - Solve each of the following systems by graphing:...Ch. 4.1 - Solve to two decimal places using graphical...Ch. 4.1 - Solve by substitution: 3x3y=22xy=6 Ch. 4.1 - Solve the following system using elimination by...Ch. 4.1 - Dennis wants to use cottage cheese and yogurt to...Ch. 4.1 - Find the equilibrium quantity and equilibrium...Ch. 4.1 - In Problems 1-6, find the x and y coordinates of...

Additional Math Textbook Solutions

Find more solutions based on key concepts

Use transformations to graph y=3 x 2 . (pp. 106-114)

Precalculus

3. Voluntary Response Sample What is a voluntary response sample, and why is such a sample generally not suitab...

Elementary Statistics

Matching In Exercises 17–20, match the level of confidence c with the appropriate confidence interval. Assume e...

Elementary Statistics: Picturing the World (7th Edition)

Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...

Algebra and Trigonometry (6th Edition)

Choose one of the answers in each case. In statistical inference, measurements are made on a (sample or popula...

Introductory Statistics

CHECK POINT I You deposit $3000 in s savings account at Yourtown Bank, which has rate of 5%. Find the interest ...

Thinking Mathematically (6th Edition)

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.

Solution Summary: The author calculates the number of guitar models produced each week using the allocations of 3,000.

Videos

Want to see the full answer?

Chapter 4 Solutions

Additional Math Textbook Solutions