Chapter 4.3, Problem 73E

Boat production. A small manufacturing plant makes three types of inflatable boats: one-person, two-person, and four-person models. Each boat requires the services of three departments, as listed in the table. The cutting, assembly, and packaging departments have available a maximum of $380,330\text{ and }120$ labor-hours per week, respectively

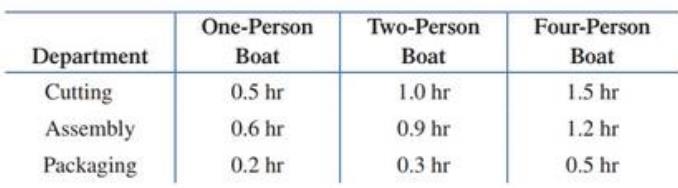
(A) How many boats of each type must be produced each week for the plant to operate at full capacity?

(B) How is the production schedule in part (A) affected if the packaging department is no longer used?

(C) How is the production schedule in part (A) affected if the four-person boat is no longer produced?