
a.
Find a trignometric model for International Falls.
a.
Answer to Problem 89E
Explanation of Solution
Given information:
The table shows the maximum daily high temperatures in Las Vegas
A model for the temperatures in Las Vegas is
Find a trignometric model for International Falls.
Calculation:
We are given with the data, which shows the maximum daily high temperatures in Las Vegas
We are given with the model of temperature in Las Vegas.
Now to model the data for International Falls,
Amplitude
Period
Also,
Because maximum temperature occurs in seventh month,
So,
The average temperature is,
Hence, the model is
b.
Graph the data points.
How well does the model fit the data?
b.
Answer to Problem 89E
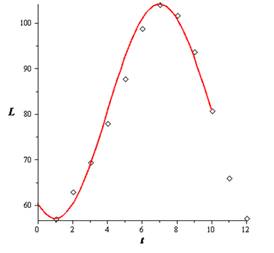
The model fits the data well.
Explanation of Solution
Given information:
The table shows the maximum daily high temperatures in Las Vegas
A model for the temperatures in Las Vegas is
Use a graphing utility to graph the data points and the model for the temperatures in Las Vegas. How well does the model fit the data?
Calculation:
Let us first plot the plots and graph the model of Las Vegas.
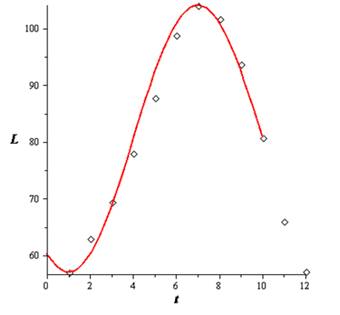
Hence, the model fits the data well.
c.
Graph the data points and the model for the temperatures in International Falls.
c.
Answer to Problem 89E

Explanation of Solution
Given information:
The table shows the maximum daily high temperatures in Las Vegas
A model for the temperatures in Las Vegas is
Use the graphing utility to graph the data points and the model for the temperatures in International Falls. How well does the model fit the data?
Calculation:
Let us first plot the plots and graph the model of International Falls.
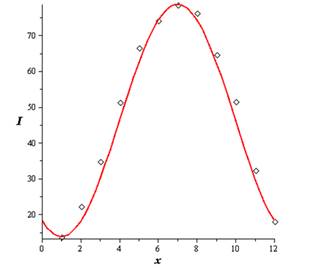
Hence, the result.
d.
Average maximum temperature.
d.
Answer to Problem 89E
Explanation of Solution
Given information:
The table shows the maximum daily high temperatures in Las Vegas
A model for the temperatures in Las Vegas is
Use the models to estimate the average maximum temperature in each city. Which term of the models did you use? Explain.
Calculation:
The annual average temperature is,
Las Vegas:
International Falls:
Hence, average temperature of Las Vegas is
e.
Period of each model.
e.
Answer to Problem 89E
Explanation of Solution
Given information:
The table shows the maximum daily high temperatures in Las Vegas
A model for the temperatures in Las Vegas is
What is the period of each model? Are the periods what you expected? Explain.
Calculation:
The period for both the model is
Yes, this is what we expected, as the number of months in a year is
Hence, the period for both the model is
f.
Which city has the greater variability in temperature throughout the year?
Factor of the models determines this variability.
f.
Answer to Problem 89E
International Falls.
Amplitude.
Explanation of Solution
Given information:
The table shows the maximum daily high temperatures in Las Vegas
A model for the temperatures in Las Vegas is
Which city has the greater variability in temperature throughout the year? Which factor of the models determines this variability? Explain
Calculation:
International Falls has greater variability,
Amplitude determines this factor.
Hence, greater the amplitude, greater is the variabilty.
Chapter 4 Solutions
Precalculus with Limits
- A Content X MindTap - Cengage Learning x Function Evaluations x + /ui/evo/index.html?elSBN=9780357038406&id=339416021&snapshotld=877369& GE MINDTAP , Limits, and the Derivative ⭑ វា a ANSWEI 16. Refer to the graph of the function f in the following figure. कर्ट AA C 54 -3-2 7 7 Ay 6. S 5. y=f(x) 4 3. 2. 1 -3- 34567 8 00 9 10 a. Find the value of ƒ (7). b. Find the values of x corresponding to the point(s) on the graph of ƒ located at a height of 5 units from the x-axis. c. Find the point on the x-axis at which the graph of ƒ crosses it. What is the value of f (x) at this point? d. Find the domain and range of f. MacBook Pro G Search or type URL + > % Λ & 5 6 7 29 ( 8 9 0arrow_forwardMorgan F. - C X A Courses MindTap - Cengage Learning Х Domain of Square Roots X + gage.com/static/nb/ui/evo/index.html?elSBN 9780357038406&id=339416021&snapshotld=877369& CENGAGE MINDTAP 2: Functions, Limits, and the Derivative 47. x if x < 0 f(x) = 2x+1 if x 0 Answerarrow_forwardA Content MindTap - Cengage Learning × Function Evaluations * + c/nb/ui/evo/index.html?elSBN 9780357038406&id=339416021&snapshotld=877369& GAGE MINDTAP ions, Limits, and the Derivative 15. Refer to the graph of the function f in the following figure. 6 y = f(x) 5 4+ 3- 2- 1 + 2 -1 3 4 5 6 a. Find the value of ƒ (0). Answer-> b. Find the value of x for which (i) f (x) = 3 and (ii) f (x) = 0. Answer ▾ c. Find the domain of f. Answer + d. Find the range of f. Answer+ MacBook Proarrow_forward
- Answer-> 12. Let g be the function defined by Find g(-2), g(0), g (2), and g (4). - +1 if x <2 g(x) = √√√x-2 if x 2arrow_forward13. Let f be the function defined by Find f (-1), f (0), ƒ (1) and ƒ (2). Answer f(x) = .2 J-x² +3 if x <1 2x²+1 2x²+1 if x ≥ 1arrow_forwardΛ Content Mind Tap - Cengage Learning × Function Evaluations x + c/nb/ui/evo/index.html?elSBN 9780357038406&id=339416021&snapshotld=877369& GAGE MINDTAP ons, Limits, and the Derivative 14. Let f be the function defined by Find f (0), f (1), and f (2). 2+1 x if x 1 if x 1 f(x) = 1 1-xarrow_forward
- A Content c/nb/ui/evo/index.html?elSBN 9780357038406&id=339416021&snapshotld=877369& GAGE MINDTAP ons, Limits, and the Derivative 11. Let f be the function defined by Find f (-2), f (0), and f (1). Answer f(x) = [ x² + 1 if x ≤ 0 if x > 0arrow_forwardGiven that 4−4i is a zero, factor the following polynomial function completely. Use the Conjugate Roots Theorem, if applicable. f(x)=x4−5x3−2x2+176x−320arrow_forwardeliminate the parameter to find the cartesian equation of the curve and sketch the graph. On the graph show the direction it takes and the initial and terminal point. Please draw by hand and show how you got to each steparrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





