
Concept explainers
a.
Use a variable to indicate the height of the balloon.
a.
Answer to Problem 76E
Explanation of Solution
Given information:
A
Show the known quantities of the triangle and use a variable to indicate the height of the balloon.
Calculation:
The height of the balloon is represented by
b.
Solve an equation for the height of the balloon.
b.
Answer to Problem 76E
Explanation of Solution
Given information:
A
Use a trigonometric function to write and solve an equation for the height of the balloon.
Calculation:
we can see that the length of the hypotenuse of the triangle is
The length of the side opposite to the angle
Now, we know that a trignometric function which involves the two sides, that is the hypotenuse and the opposite side to the angle is the sine function.
Consider a right triangle, with one acute angle
Substituting the values in the above given formula of sin, we have,
Hence, the equation invoolving the unknown quantity
c.
How does this affect the triangle you drew in part (a)?
c.
Answer to Problem 76E
The angle the ballon makes with the ground becomes smaller.
Explanation of Solution
Given information:
A
The breeze becomes stronger and the angle the line makes with the ground decreases. How does this affect the triangle you drew in part (a)?
Calculation:
In order to find the height of the balloon,
Hence,
Now,
Substitute this in equation of
Hence, the height of the ballon is
As the breeza becomes stronger, the hypotenuse of the triangle drwan above tilts more to the ground and hence the angle the ballon makes with the ground becomes smaller. As such the height of the ballon also decreases.
angle
Hence, the angle the ballon makes with the ground becomes smaller.
d.
Complete the table, which shows the heights (in meters) of the balloon for decreasing angle measures
d.
Answer to Problem 76E
Explanation of Solution
Given information:
A
Complete the table, which shows the heights (in meters) of the balloon for decreasing angle measures
Calculation:
We have to find the height of the ballon for decreasing angle measures
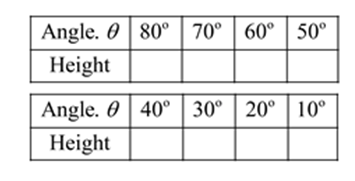
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence,for
For
Let us use the equation involving the height
Hence, for
For
Let us use the equation involving the height
Hence, for
e.
As
e.
Answer to Problem 76E
The height also approaches zero.
Explanation of Solution
Given information:
A
As
Calculation:
This is because, the height
Hence, we can clearly see that as
Chapter 4 Solutions
Precalculus with Limits
- A cable runs along the wall from C to P at a cost of $24 per meter, and straight from P to M at a cost of $26 per meter. If M is 10 meters from the nearest point A on the wall where P lies, and A is 72 meters from C, find the distance from C to P such that the cost of installing the cable is minimized and find this cost. C 72 P A 10 Marrow_forwardThe number of bank robberies in a country for the years 2010-2018 is given in the following figure. Consider the closed interval [2010,2018]. (a) Give all relative maxima and minima and when they occur on the interval. (b) Give the absolute maxima and minima and when they occur on the interval. Incidents 7000- 6000-5 5482 5000- 4424 4273 4822 4000- 3708 3748 4229 4089 3000- 2582 2000- 1000- 0 2010 2012 2014 2016 2018 Yeararrow_forwardplease do 8.1 q7arrow_forward
- please do 8.1 q6arrow_forwardIf the price charged for a candy bar is p(x) cents, then x thousand candy bars will be sold in a certain city, where p(x)=158- X 10° a. Find an expression for the total revenue from the sale of x thousand candy bars. b. Find the value of x that leads to maximum revenue. c. Find the maximum revenue.arrow_forward3 The total profit P(X) (in thousands of dollars) from the sale of x hundred thousand automobile tires is approximated by P(x) = -x³ + 12x² + 60x - 200, x≥5. Find the number of hundred thousands of tires that must be sold to maximize profit. Find the maximum profit. The maximum profit is $ when hundred thousand tires are sold.arrow_forward
- A fence must be built to enclose a rectangular area of 5000 ft². Fencing material costs $4 per foot for the two sides facing north and south and $8 per foot for the other two sides. Find the cost of the least expensive fence. The cost of the least expensive fence is $ (Simplify your answer.)arrow_forwardThe number of fish swimming upstream to spawn is approximated by the function given below, where x represents the temperature of the water in degrees Celsius. Find the water temperature that produces the maximum number of fish swimming upstream. F(x) = x3 + 3x² + 360x + 5017, 5≤x≤18arrow_forwardA campground owner has 500 m of fencing. He wants to enclose a rectangular field bordering a river, with no fencing along the river. (See the sketch.) Let x represent the width of the field. (a) Write an expression for the length of the field as a function of x. (b) Find the area of the field (area = length x width) as a function of x. (c) Find the value of x leading to the maximum area. (d) Find the maximum area. x Riverarrow_forward
- A rectangular tank with a square base, an open top, and a volume of 1372 ft³ is to be constructed of sheet steel. Find the dimensions of the tank that has the minimum surface area. The dimensions of the tank with minimum surface area are (Simplify your answer. Use a comma to separate answers.) ft.arrow_forwardWrite an equation for the function graphed below 5+ 4 - -7 -6 -5 -4 -3 -2 -1 y = 3. 2 1 + 1 2 3 4 5 6 7 -1 -3 -4 5 -5+ aarrow_forwardApproximate graphically the radius and height of a cylindrical container with volume 50 cubic inches and lateral surface area 75 square inches. h 2лr The radius is in and the height is in. (Round to the nearest hundredth.) h Volume of a cylinder = r²h Lateral area of a cylinder = 2лrharrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





