Chapter 4.5, Problem 88E

a.

To determine

To find: a trigonometric model for C.

Answer to Problem 88E

  $C(t)=56.1+27.6\sin (0.483t-1.862).$

Explanation of Solution

Given information: A model for the temperature in Q is given by,

  $Q(t)=57.5+0.6\sin (0.566x-2.568).$ The table shows the average daily high temperature.

(in degree Fahrenheit) for Q and C for month t , with t =1 corresponding to January .

Month t	Q	C
1	47.1	31.0
2	49.1	35.3
3	51.4	46.6
4	54.8	59.0
5	59.5	70.0
6	63.1	79.7
7	67.4	84.1
8	68.6	81.9
9	66.2	74.8
10	58.2	62.3
11	50.3	48.2
12	46.0	34.8

Calculation:

  $Q(t)=57.5+0.6\sin (0.566x-2.568).$

From the table data trigonometric model for C is,

  $C(t)=56.1+27.6\sin (0.483t-1.862).$

b.

To determine

To graph: the data and the model for the temperature in Q using graphing utility and to find how the model fits the data.

Answer to Problem 88E

The model does not fit the data well.

Explanation of Solution

Given information: A model for the temperature in Q is given by,

  $Q(t)=57.5+0.6\sin (0.566x-2.568).$ The table shows the average daily high temperature.

(in degree Fahrenheit) for Q and C for month t , with t =1 corresponding to January .

Month t	Q	C
1	47.1	31.0
2	49.1	35.3
3	51.4	46.6
4	54.8	59.0
5	59.5	70.0
6	63.1	79.7
7	67.4	84.1
8	68.6	81.9
9	66.2	74.8
10	58.2	62.3
11	50.3	48.2
12	46.0	34.8

The graph of $Q(t)=57.5+0.6\sin (0.566x-2.568).$using graphing utility is given below

  

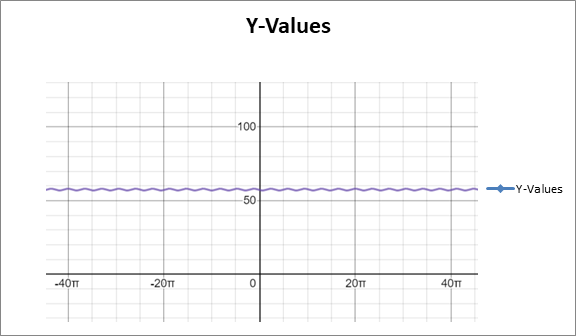
Calculation:

It is clear from the graph that the model does not fit the data well.

c.

To determine

To graph : the data and the model for the temperature in C using graphing utility and to find how does the model fit the data.

Answer to Problem 88E

The model fits the data well.

Explanation of Solution

Given information: A model for the temperature in Q is given by,

  $Q(t)=57.5+0.6\sin (0.566x-2.568).$ The table shows the average daily high temperature.

(in degree Fahrenheit) for Q and C for month t , with t =1 corresponding to January .

Month t	Q	C
1	47.1	31.0
2	49.1	35.3
3	51.4	46.6
4	54.8	59.0
5	59.5	70.0
6	63.1	79.7
7	67.4	84.1
8	68.6	81.9
9	66.2	74.8
10	58.2	62.3
11	50.3	48.2
12	46.0	34.8

Calculation:

From the table data $C(t)=56.1+27.6\sin (0.483t-1.862).$ The graph of C(t) using

graphing utility is given below.

  

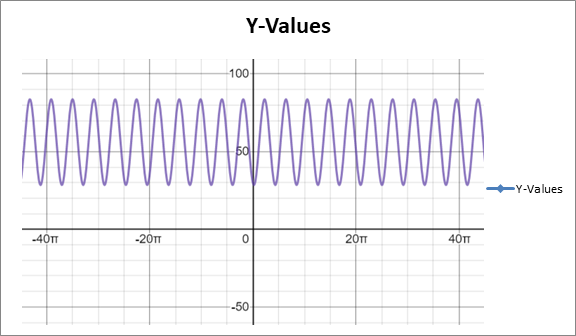
It is clear from the graph that the model fits the data well.

d.

To determine

To : use the models to estimate the average daily high temperature in each city.

Answer to Problem 88E

So, C average daily high temperature is 84 degrees.

Explanation of Solution

Given information: A model for the temperature in Q is given by,

  $Q(t)=57.5+0.6\sin (0.566x-2.568).$ The table shows the average daily high temperature.

(in degree Fahrenheit) for Q and C for month t , with t =1 corresponding to January .

Month t	Q	C
1	47.1	31.0
2	49.1	35.3
3	51.4	46.6
4	54.8	59.0
5	59.5	70.0
6	63.1	79.7
7	67.4	84.1
8	68.6	81.9
9	66.2	74.8
10	58.2	62.3
11	50.3	48.2
12	46.0	34.8

Calculation:

C average daily high temperature = $\frac{\text{Sum}\text{of}\text{all}\text{temperature}\text{values}\text{form}\text{table}\text{for}\text{C}}{12}=84$ .

So, C average daily high temperature is 84 degrees.

e.

To determine

To : find the period of each model.

Answer to Problem 88E

C period=13.0, Q period=11.4.

Explanation of Solution

Given information: A model for the temperature in Q is given by,

  $Q(t)=57.5+0.6\sin (0.566x-2.568).$ The table shows the average daily high temperature.

(in degree Fahrenheit) for Q and C for month t , with t =1 corresponding to January .

Month t	Q	C
1	47.1	31.0
2	49.1	35.3
3	51.4	46.6
4	54.8	59.0
5	59.5	70.0
6	63.1	79.7
7	67.4	84.1
8	68.6	81.9
9	66.2	74.8
10	58.2	62.3
11	50.3	48.2
12	46.0	34.8

Calculation:

From the table data,

C period=13.0, Q period=11.4.

f.

To determine

To: find which city has the greatest variability in temperature throughout the year..

Answer to Problem 88E

C has a greater temperature variability because it has a greater amplitude (27.6) compared to Q (11.1).

Explanation of Solution

Given information: A model for the temperature in Q is given by,

  $Q(t)=57.5+0.6\sin (0.566x-2.568).$ The table shows the average daily high temperature.

(in degree Fahrenheit) for Q and C for month t , with t =1 corresponding to January .

Month t	Q	C
1	47.1	31.0
2	49.1	35.3
3	51.4	46.6
4	54.8	59.0
5	59.5	70.0
6	63.1	79.7
7	67.4	84.1
8	68.6	81.9
9	66.2	74.8
10	58.2	62.3
11	50.3	48.2
12	46.0	34.8

Calculation:

From the table data C has a greater temperature variability because it has a greater amplitude (27.6) compared to Q (11.1).