
Imports and exports: The following table presents the U.S. imports and exports (in billions of dollars) for each of 29 months.
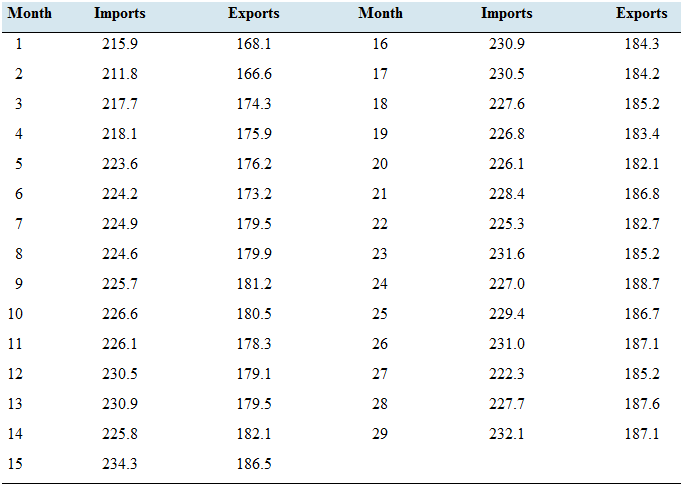
- Compute the least-squares regression line for predicting exports (y) from imports (x).
- Compute the coefficient of determination.
- The months two lowest exports are months 1 and 2. when the exports were 168.1 and 166.6, respectively. Remove these points and compute the least-squares regression line. Is die result noticeably different?
- Compute the coefficient of determination for the data set months 1 and 2 removed.
- Two economists decide to study the relationship between imports and exports. One uses data from months 1 through 29 and the other uses data from months 3 through 29. For which data set will the proportion of variance explained by the least-squares regression line be greater?
a.
To find: The least-square regression line for the given data set.
Answer to Problem 26E
The least square regression line of the given data set is,
Explanation of Solution
Given:
The import and exports of United States within
Calculation:
The least-square regression is given by the formula,
Where
The correlation coefficient is given by the formula,
Considering the exports as

The correlation coefficient can be obtained by the following table.
| x | y | Zx | Zy | ZxZy |
| 215.9 | 168.1 | -1.99175 | -2.32277 | 4.626396 |
| 211.8 | 166.6 | -2.79101 | -2.58707 | 7.220549 |
| 217.7 | 174.3 | -1.64086 | -1.23035 | 2.018834 |
| 218.1 | 175.9 | -1.56288 | -0.94844 | 1.482294 |
| 223.6 | 176.2 | -0.49071 | -0.89558 | 0.439465 |
| 224.2 | 173.2 | -0.37374 | -1.42417 | 0.532271 |
| 224.9 | 179.5 | -0.23728 | -0.31412 | 0.074536 |
| 224.6 | 179.9 | -0.29576 | -0.24365 | 0.072062 |
| 225.7 | 181.2 | -0.08133 | -0.01459 | 0.001187 |
| 226.6 | 180.5 | 0.094118 | -0.13793 | -0.01298 |
| 226.1 | 178.3 | -0.00335 | -0.52556 | 0.001762 |
| 230.5 | 179.1 | 0.854389 | -0.3846 | -0.3286 |
| 230.9 | 179.5 | 0.932365 | -0.31412 | -0.29288 |
| 225.8 | 182.1 | -0.06184 | 0.143989 | -0.0089 |
| 234.3 | 186.5 | 1.595165 | 0.919257 | 1.466367 |
| 230.9 | 184.3 | 0.932365 | 0.531623 | 0.495667 |
| 230.5 | 184.2 | 0.854389 | 0.514003 | 0.439158 |
| 227.6 | 185.2 | 0.289059 | 0.6902 | 0.199509 |
| 226.8 | 183.4 | 0.133106 | 0.373045 | 0.049655 |
| 226.1 | 182.1 | -0.00335 | 0.143989 | -0.00048 |
| 228.4 | 186.8 | 0.445012 | 0.972116 | 0.432603 |
| 225.3 | 182.7 | -0.15931 | 0.249707 | -0.03978 |
| 231.6 | 185.2 | 1.068824 | 0.6902 | 0.737703 |
| 227 | 188.7 | 0.172094 | 1.306891 | 0.224908 |
| 229.4 | 186.7 | 0.639953 | 0.954496 | 0.610833 |
| 231 | 187.1 | 0.951859 | 1.024975 | 0.975632 |
| 222.3 | 185.2 | -0.74413 | 0.6902 | -0.5136 |
| 227.7 | 187.6 | 0.308553 | 1.113074 | 0.343442 |
| 232.1 | 187.1 | 1.166295 | 1.024975 | 1.195423 |
The sum of
Hence, the correlation coefficient is,
Then, the coefficient
Therefore,
Conclusion:
The least square regression line is found to be,
b.
To calculate: The coefficient of determination.
Answer to Problem 26E
The coefficient of determination is found to be,
Explanation of Solution
Calculation:
The correlation coefficient
The coefficient of determination is calculated by taking the square of the correlation coefficient.
Therefore, the coefficient of determination should be,
Simplifying the square,
Conclusion:
Therefore, the coefficient of determination is found to be
c.
To find:The least-square regression line without considering the lowest two exports.
Answer to Problem 26E
The least square regression line of the given data set is,
Explanation of Solution
Calculation:
From the all
The statistics should be calculated again for the current data set, imports and exports of last

The calculations can be completed using a table.
| x | y | Zx | Zy | ZxZy |
| 217.7 | 174.3 | -2.36254 | -1.85805 | 4.389725 |
| 218.1 | 175.9 | -2.26121 | -1.48713 | 3.362707 |
| 223.6 | 176.2 | -0.86789 | -1.41758 | 1.230299 |
| 224.2 | 173.2 | -0.71589 | -2.11306 | 1.512718 |
| 224.9 | 179.5 | -0.53856 | -0.65255 | 0.351434 |
| 224.6 | 179.9 | -0.61456 | -0.55982 | 0.344039 |
| 225.7 | 181.2 | -0.33589 | -0.25844 | 0.086808 |
| 226.6 | 180.5 | -0.10789 | -0.42072 | 0.045393 |
| 226.1 | 178.3 | -0.23456 | -0.93074 | 0.218314 |
| 230.5 | 179.1 | 0.880098 | -0.74528 | -0.65592 |
| 230.9 | 179.5 | 0.98143 | -0.65255 | -0.64043 |
| 225.8 | 182.1 | -0.31056 | -0.0498 | 0.015465 |
| 234.3 | 186.5 | 1.842756 | 0.970245 | 1.787925 |
| 230.9 | 184.3 | 0.98143 | 0.460224 | 0.451678 |
| 230.5 | 184.2 | 0.880098 | 0.437042 | 0.384639 |
| 227.6 | 185.2 | 0.145437 | 0.668869 | 0.097279 |
| 226.8 | 183.4 | -0.05723 | 0.251579 | -0.0144 |
| 226.1 | 182.1 | -0.23456 | -0.0498 | 0.01168 |
| 228.4 | 186.8 | 0.348102 | 1.039794 | 0.361955 |
| 225.3 | 182.7 | -0.43722 | 0.0893 | -0.03904 |
| 231.6 | 185.2 | 1.158762 | 0.668869 | 0.77506 |
| 227 | 188.7 | -0.00656 | 1.480266 | -0.00971 |
| 229.4 | 186.7 | 0.601433 | 1.016611 | 0.611424 |
| 231 | 187.1 | 1.006763 | 1.109342 | 1.116845 |
| 222.3 | 185.2 | -1.19722 | 0.668869 | -0.80078 |
| 227.7 | 187.6 | 0.170771 | 1.225256 | 0.209238 |
| 232.1 | 187.1 | 1.285427 | 1.109342 | 1.425979 |
The sum the values in the right most column is found to be,
Hence, the correlation coefficient is,
Then, the coefficient
Therefore,
Conclusion:
The least square regression line is found to be,
d.
To calculate: The coefficient of determination for the last
Answer to Problem 26E
The coefficient of determination is found to be,
Explanation of Solution
Calculation:
The correlation coefficient
The coefficient of determination is calculated by taking the square of the correlation coefficient.
Simplifying the square,
Conclusion:
Therefore, the coefficient of determination is found to be
e.
To find: The data set which
Answer to Problem 26E
The data set with all
Explanation of Solution
Calculation:
The coefficient of determination for the all
Then, the coefficient of determination for the
The coefficient of determination denotes the proportion of variance that is explained by the least-square regression line.
For the all
Conclusion:
Since
Want to see more full solutions like this?
Chapter 4 Solutions
ELEMENTARY STATISTICS W/CONNECT >C<
- Olympic Pole Vault The graph in Figure 7 indicates that in recent years the winning Olympic men’s pole vault height has fallen below the value predicted by the regression line in Example 2. This might have occurred because when the pole vault was a new event there was much room for improvement in vaulters’ performances, whereas now even the best training can produce only incremental advances. Let’s see whether concentrating on more recent results gives a better predictor of future records. (a) Use the data in Table 2 (page 176) to complete the table of winning pole vault heights shown in the margin. (Note that we are using x=0 to correspond to the year 1972, where this restricted data set begins.) (b) Find the regression line for the data in part ‚(a). (c) Plot the data and the regression line on the same axes. Does the regression line seem to provide a good model for the data? (d) What does the regression line predict as the winning pole vault height for the 2012 Olympics? Compare this predicted value to the actual 2012 winning height of 5.97 m, as described on page 177. Has this new regression line provided a better prediction than the line in Example 2?arrow_forwardWhat does the y -intercept on the graph of a logistic equation correspond to for a population modeled by that equation?arrow_forwardCellular Phone Subscribers The table shows the numbers of cellular phone subscribers y in millions in the United States from 2008 through 2013. Source: CTIA- The Wireless Association Year200820092010201120122013Number,y270286296316326336 (a) Find the least squares regression line for the data. Let x represent the year, with x=8 corresponding to 2008. (b) Use the linear regression capabilities of a graphing utility to find a linear model for the data. How does this model compare with the model obtained in part a? (c) Use the linear model to create a table of estimated values for y. Compare the estimated values with the actual data.arrow_forward
- We have data from 209 publicly traded companies (circa 2010) indicating sales and compensation information at the firm-level. We are interested in predicting a company's sales based on the CEO's salary. The variable sales; represents firm i's annual sales in millions of dollars. The variable salary; represents the salary of a firm i's CEO in thousands of dollars. We use least-squares to estimate the linear regression sales; = a + ßsalary; + ei and get the following regression results: regress sales salary . Source Model Residual Total sales salary _cons SS 337920405 2.3180e+10 2.3518e+10 df 1 207 208 Coef. Std. Err. .9287785 .5346574 5733.917 1002.477 MS 337920405 111980203 113066454 t Number of obs F(1, 207) Prob> F R-squared Adj R-squared Root MSE P>|t| 1.74 0.084 5.72 0.000 209 3.02 -.1252934 3757.543 0.0838 0.0144 0.0096 10582 [95% Conf. Interval] 1.98285 7710.291 This output tells us the regression line equation is sales = 5,733.917 +0.9287785 salary. Suppose a CEO of a company…arrow_forwardWe have data from 209 publicly traded companies (circa 2010) indicating sales and compensation information at the firm-level. We are interested in predicting a company's sales based on the CEO's salary. The variable sales; represents firm i's annual sales in millions of dollars. The variable salary; represents the salary of a firm i's CEO in thousands of dollars. We use least-squares to estimate the linear regression sales; = a + ßsalary; + ei and get the following regression results: . regress sales salary Source Model Residual Total sales salary cons SS 337920405 2.3180e+10 2.3518e+10 df 1 207 208 Coef. Std. Err. .9287785 .5346574 5733.917 1002.477 MS 337920405 111980203 113066454 Number of obs F (1, 207) Prob > F R-squared t P>|t| = Adj R-squared = Root MSE 1.74 0.084 5.72 0.000 = = -.1252934 3757.543 = 209 3.02 0.0838 0.0144 0.0096 10582 [95% Conf. Interval] 1.98285 7710.291 This output tells us the regression line equation is sales = 5,733.917 +0.9287785 salary. Interpret the…arrow_forwardFor major league baseball teams, do higher player payrolls mean more gate money? Here are data for each of the American League teams in the year 2002. The variable x denotes the player payroll (in millions of dollars) for the year 2002, and the variable y denotes the mean attendance (in thousands of fans) for the 81 home games that year. The data are plotted in the scatter plot below, as is the least-squares regression line. The equation for this line is y = 11.43 + 0.23x. Player payroll, x (in Mean attendance, y (in $1,000,000s) thousands) Anaheim 62.8 28.52 Baltimore 56.5 33.09 40- Boston 110.2 32.72 35 Chicago White Sox 54.5 20.74 30- Cleveland 74.9 32.35 25- Detroit 54.4 18.52 Kansas City 49.4 16.30 15- Minnesota 41.3 23.70 10+ New York Yankees 133.4 42.84 Oakland 41.9 26.79 20 40 60 80 100 120 140 Seattle 86.1 43.70 Player payroll, Тarmpa Bay 34.7 13.21 X (in $1,000,000s) Техas 106.9 29.01 Toronto 66.8 20.25 Send data to calculator Send data to Excel Based on the sample data and…arrow_forward
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill





