Chapter 4.2, Problem 25E

Logistic Growth Animal populations are not capable of unrestricted growth because of limited habitat and food supplies. Under such conditions the population follows a logistic growth model:

$P(t)=\frac{d}{1+k{e}^{-ct}}$

where c, d, and k are positive constants. For a certain fish population in a small pond d = 1200, k = 11, c = 0.2, and t is measured in years. The fish were introduced into the pond at time t = 0.

1. (a) How many fish were originally put in the pond?
2. (b) Find the population after 10, 20, and 30 years.
3. (c) Evaluate P(t) for large values of t. What value does the population approach as t → ∞? Does the graph shown confirm your calculations?

To determine

The numbers of fish were originally put in the pond.

Answer to Problem 25E

The numbers of fish were originally put in the pond is $100$.

Explanation of Solution

Given:

The fish population follows the logistic growth model

$P\left(t\right)=\frac{d}{1+k{e}^{-ct}}$

Where,

• c, d and k are positive constants.

Calculations:

The fish population follows the logistic growth model

$P\left(t\right)=\frac{d}{1+k{e}^{-ct}}$

Substitute 0 for t, 1200 for d, 0.2 for c 11 for k in the above formula to calculate the numbers of fish were originally put in the pond.

$\begin{array}{c}P\left(0\right)=\frac{1200}{1+11\times e^{-\left(0.2\times 0\right)}}\left[\because e=2.718\right]\\ =\frac{1200}{1+11\times {2.718}^0}\\ =\frac{1200}{12}\\ =100\end{array}$

Hence, the numbers of fish were originally put in the pond is $100$

To determine

The population of fish in the pond after 10, 20 and 30 years.

Answer to Problem 25E

The population fish after 30 years in the pond. is $1168$.

Explanation of Solution

Given:

The fish population follows the logistic growth model

$P\left(t\right)=\frac{d}{1+k{e}^{-ct}}$

Where,

• c, d and k are positive constants.

Calculations:

The fish population follows the logistic growth model

$P\left(t\right)=\frac{d}{1+k{e}^{-ct}}$

Substitute 10 for t, 1200 for d, 0.2 for c 11 for k in the above formula to calculate the population of fish after 10 years in the pond.

$\begin{array}{c}P\left(10\right)=\frac{1200}{1+11\times e^{-\left(0.2\times 10\right)}}\left[\because e=2.718\right]\\ =\frac{1200}{1+11\times {2.718}^{-2}}\\ =\frac{1200}{2.48}\\ =482.18\approx 482\end{array}$

Hence, the population fish after 10 years in the pond. is $482$

Now, Substitute 20 for t, 1200 for d, 0.2 for c 11 for k in the above formula to calculate the population of fish after 20 years in the pond.

$\begin{array}{c}P\left(20\right)=\frac{1200}{1+11\times e^{-\left(0.2\times 20\right)}}\left[\because e=2.718\right]\\ =\frac{1200}{1+11\times {2.718}^{-4}}\\ =\frac{1200}{1.20}\\ =998.82\approx 999\end{array}$

Hence, the population fish after 20 years in the pond. is $999$

Now, Substitute 30 for t, 1200 for d, 0.2 for c 11 for k in the above formula to calculate the population of fish after 30 years in the pond.

$\begin{array}{c}P\left(30\right)=\frac{1200}{1+11\times e^{-\left(0.2\times 30\right)}}\left[\because e=2.718\right]\\ =\frac{1200}{1+11\times {2.718}^{-6}}\\ =\frac{1200}{1.02}\\ =1168.1\approx 1168\end{array}$

Hence, the population fish after 30 years in the pond. is $1168$

To determine

To Evaluate: The population of fish for larger value of t.

Answer to Problem 25E

The population of fish for larger value of t is $1200$.

Explanation of Solution

Given:

The fish population follows the logistic growth model shown below,

$P\left(t\right)=\frac{d}{1+k{e}^{-ct}}$

Calculation:

The fish population follows the logistic growth model shown below,

$P\left(t\right)=\frac{d}{1+k{e}^{-ct}}$

The graph of the function $P\left(t\right)$ is shown Figure (1),

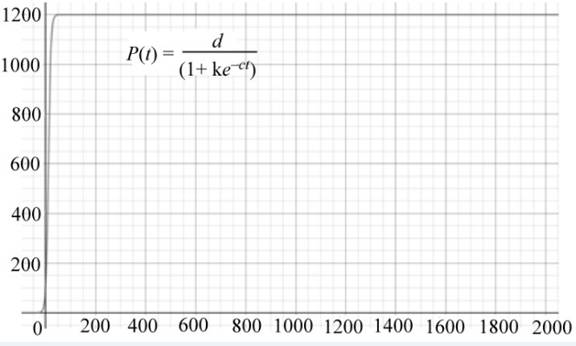
Figure (1)

From the Figure (1) 1200 is the highest population at $t=\infty$

Confirm the highest population 1200 By calculation,

Substitute $\infty$ for t, 1200 for d, 0.2 for c 11 for k in the above formula to calculate the population of fish after $\infty$ years in the pond.

$\begin{array}{c}P\left(\infty \right)=\frac{1200}{1+11\times e^{-\left(0.2\times \infty \right)}}\left[\because e=2.718\right]\\ =\frac{1200}{1+11\times {2.718}^{-\infty }}\\ =\frac{1200}{1}\\ =1200\end{array}$

Hence, the population of fish for larger value of t is $1200$.