Chapter 4, Problem 9P

(a)

To determine

To sketch: The scatter plot of the data point $\left(x,y\right)$.

Explanation of Solution

Given:

The data is as shown below.

$x$	$y$
2	0.08
4	0.12
6	0.18
8	0.25
10	0.36
12	0.52
14	0.73
16	1.06

The scatter plot of the data $\left(x,y\right)$ listed in the table as shown below in Figure 1.

Form Figure 1, it is noticed that the scatter plot of the data $\left(x,y\right)$ listed in the table is an increasing curve.

(b)

To determine

To sketch: The scatter plots of $\left(x,\ln y\right)$ and $\left(\ln x,\ln y\right)$ of the data $\left(x,y\right)$ listed in table.

Explanation of Solution

Given:

$x$	$y$
2	0.08
4	0.12
6	0.18
8	0.25
10	0.36
12	0.52
14	0.73
16	1.06

The table of $\left(x,\ln y\right)$ and $\left(\ln x,\ln y\right)$ of the data point $\left(x,y\right)$ is listed below.

$x$	$y$	$\ln x$	$\ln y$
2	0.08	0.69315	-2.52573
4	0.12	1.38629	-2.12026
6	0.18	1.79176	-1.7148
8	0.25	2.07944	-1.38629
10	0.36	2.30259	-1.02165
12	0.52	2.48491	-0.65393
14	0.73	2.63906	-0.31471
16	1.06	2.77259	0.05827

Use online graphing calculator and draw the scatter plot of “ $x$ verses $\ln y$”  as shown below in Figure 2.

From Figure 2, it is noticed that the scatter plot of “ $x$ verses $\ln y$”  is an increasing function.

On the same manner, use online graphing calculator and draw the scatter plot of “ $\ln x$ verses $\ln y$”  as shown below in Figure 3.

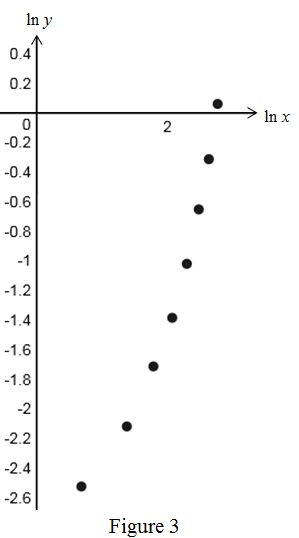
From Figure 3, it is noticed that the scatter plot of “ $\ln x$ verses $\ln y$” is an increasing function.

(c)

To determine

To find: The function which is more appropriate for modeling of this data, exponential or power function.

Explanation of Solution

The exponential function $y=0.0577\times {1.2}^x$ is more appropriate for modeling of this data.

Use online graphing calculator and draw graph of exponential function and power function on the scatter plot as shown below in Figure 4.

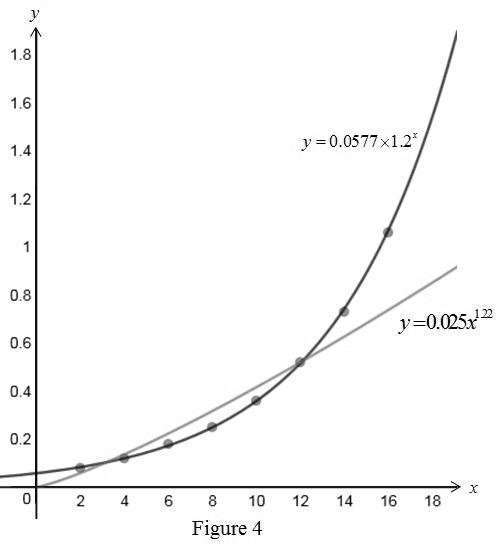
In Figure 4, the black line curve represents the exponential $y=0.0577\times {1.2}^x$ function and the grey line curve represents the power function $y=0.025x^{1.22}$.

From Figure 4, it is also noticed that the exponential curve $y=0.0577\times {1.2}^x$ best fits the data points as compared to the power function $y=0.025x^{1.22}$, because of the exponential curve passes through all the points of the data.

Therefore, the exponential function $y=0.0577\times {1.2}^x$ is more appropriate for modeling of this data.

(d)

To determine

To find: The appropriate function to model the data.

Answer to Problem 9P

The exponential model $y=0.0577\times {1.2}^x$ best fits of the data.

Explanation of Solution

Given:

The data is listed as follows.

$x$	$y$
2	0.08
4	0.12
6	0.18
8	0.25
10	0.36
12	0.52
14	0.73
16	1.06

From part (c), in the Figure 4, it is noticed that the exponential function of the form $y=a{b}^x$ that gives the best fits of the data point is $y=0.0577\times {1.2}^x$, because this exponential almost passes through all the data points.

Therefore, the exponential model $y=0.0577\times {1.2}^x$ gives best fits of the data.