
Concept explainers
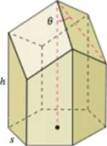
Honeycomb The surface area of a cell in a honeycomb is
where h and s are positive constants and is the angle at which the upper faces meet the altitude of the cell (see figure). Find the angle
Trending nowThis is a popular solution!

Chapter 4 Solutions
Calculus: Early Transcendental Functions (MindTap Course List)
- This question builds on an earlier problem. The randomized numbers may have changed, but have your work for the previous problem available to help with this one. A 4-centimeter rod is attached at one end to a point A rotating counterclockwise on a wheel of radius 2 cm. The other end B is free to move back and forth along a horizontal bar that goes through the center of the wheel. At time t=0 the rod is situated as in the diagram at the left below. The wheel rotates counterclockwise at 1.5 rev/sec. At some point, the rod will be tangent to the circle as shown in the third picture. B A B at some instant, the piston will be tangent to the circle (a) Express the x and y coordinates of point A as functions of t: x= 2 cos(3πt) and y= 2 sin(3πt) (b) Write a formula for the slope of the tangent line to the circle at the point A at time t seconds: -cot (3πt) (c) Express the x-coordinate of the right end of the rod at point B as a function of t: 2 cos(3πt) +41/1 (d) Express the slope of the rod…arrow_forward4. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.024. Find the approximations Tη, Mn, and S, to the integral computer algebra system.) ASK YOUR TEACHER PRACTICE ANOTHER 4 39 √ dx for n = 6 and 12. Then compute the corresponding errors ET, EM, and Es. (Round your answers to six decimal places. You may wish to use the sum command on a n Tn Mn Sp 6 12 n ET EM Es 6 12 What observations can you make? In particular, what happens to the errors when n is doubled? As n is doubled, ET and EM are decreased by a factor of about Need Help? Read It ' and Es is decreased by a factor of aboutarrow_forward6. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.001. ASK YOUR TEACHER PRACTICE ANOTHER Let I = 4 f(x) dx, where f is the function whose graph is shown. = √ ² F(x 12 4 y f 1 2 (a) Use the graph to find L2, R2 and M2. 42 = R₂ = M₂ = 1 x 3 4arrow_forward
- practice problem please help!arrow_forwardFind a parameterization for a circle of radius 4 with center (-4,-6,-3) in a plane parallel to the yz plane. Write your parameterization so the y component includes a positive cosine.arrow_forward~ exp(10). A 3. Claim number per policy is modelled by Poisson(A) with A sample x of N = 100 policies presents an average = 4 claims per policy. (i) Compute an a priory estimate of numbers of claims per policy. [2 Marks] (ii) Determine the posterior distribution of A. Give your argument. [5 Marks] (iii) Compute an a posteriori estimate of numbers of claims per policy. [3 Marks]arrow_forward
- 2. The size of a claim is modelled by F(a, λ) with a fixed a a maximum likelihood estimate of A given a sample x with a sample mean x = 11 = 121. Give [5 Marks]arrow_forwardRobbie Bearing Word Problems Angles name: Jocelyn date: 1/18 8K 2. A Delta airplane and an SouthWest airplane take off from an airport at the same time. The bearing from the airport to the Delta plane is 23° and the bearing to the SouthWest plane is 152°. Two hours later the Delta plane is 1,103 miles from the airport and the SouthWest plane is 1,156 miles from the airport. What is the distance between the two planes? What is the bearing from the Delta plane to the SouthWest plane? What is the bearing to the Delta plane from the SouthWest plane? Delta y SW Angles ThreeFourthsMe MATH 2arrow_forwardFind the derivative of the function. m(t) = -4t (6t7 - 1)6arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

