Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 4.1, Problem 5E
For Exercises 5 to 8, MNPQ is a parallelogram with diagonals
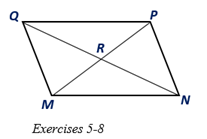
| a) If
|
b) If
|
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A tournament is a complete directed graph, for each pair of vertices x, y either (x, y) is an arc or
(y, x) is an arc. One can think of this as a round robin tournament, where the vertices represent
teams, each pair plays exactly once, with the direction of the arc indicating which team wins.
(a) Prove that every tournament has a direct Hamiltonian path. That is a labeling of the teams
V1, V2,..., Un so that vi beats Vi+1. That is a labeling so that team 1 beats team 2, team 2
beats team 3, etc.
(b) A digraph is strongly connected if there is a directed path from any vertex to any other
vertex. Equivalently, there is no partition of the teams into groups A, B so that every team
in A beats every team in B. Prove that every strongly connected tournament has a directed
Hamiltonian cycle. Use this to show that for any team there is an ordering as in part (a) for
which the given team is first.
(c) A king in a tournament is a vertex such that there is a direct path of length at most 2 to
any…
The following is known. The complete graph K2t on an even number of vertices has a 1-
factorization (equivalently, its edges can be colored with 2t - 1 colors so that the edges incident
to each vertex are distinct). This implies that the complete graph K2t+1 on an odd number of
vertices has a factorization into copies of tK2 + K₁ (a matching plus an isolated vertex).
A group of 10 people wants to set up a 45 week tennis schedule playing doubles, each week, the
players will form 5 pairs. One of the pairs will not play, the other 4 pairs will each play one
doubles match, two of the pairs playing each other and the other two pairs playing each other.
Set up a schedule with the following constraints: Each pair of players is a doubles team exactly 4
times; during those 4 matches they see each other player exactly once; no two doubles teams play
each other more than once.
(a) Find a schedule. Hint - think about breaking the 45 weeks into 9 blocks of 5 weeks. Use
factorizations of complete…
. The two person game of slither is played on a graph. Players 1 and 2 take turns, building a path in the graph. To start, Player 1 picks a vertex. Player 2 then picks an edge incident to the vertex. Then, starting with Player 1, players alternate turns, picking a vertex not already selected that is adjacent to one of the ends of the path created so far. The first player who cannot select a vertex loses. (This happens when all neighbors of the end vertices of the path are on the path.) Prove that Player 2 has a winning strategy if the graph has a perfect matching and Player 1 has a winning strategy if the graph does not have a perfect matching. In each case describe a strategy for the winning player that guarantees that they will always be able to select a vertex. The strategy will be based on using a maximum matching to decide the next choice, and will, for one of the cases involve using the fact that maximality means no augmenting paths. Warning, the game slither is often described…
Chapter 4 Solutions
Elementary Geometry for College Students
Ch. 4.1 - ABCD is a parallelogram. a Using a ruler, compare...Ch. 4.1 - ABCD is a parallelogram. a Using a ruler, compare...Ch. 4.1 - MNPQ is a parallelogram. Suppose that MQ=5, MN=8,...Ch. 4.1 - MNPQ is a parallelogram. Suppose that MQ=12.7,...Ch. 4.1 - For Exercises 5 to 8, MNPQ is a parallelogram with...Ch. 4.1 - For Exercises 5 to 8, MNPQ is a parallelogram with...Ch. 4.1 - For Exercises 5 to 8, MNPQ is a parallelogram with...Ch. 4.1 - For Exercises 5 to 8, MNPQ is a parallelogram with...Ch. 4.1 - Given that AB=3x+2, BC=4x+1, and CD=5x-2, find the...Ch. 4.1 - Given that mA=2x+3, and mC=3x-27, find the measure...
Ch. 4.1 - Given that mA=2x+3, and mB=3x-23, find the measure...Ch. 4.1 - Given that mA=2x5, and mB=x2, find the measure of...Ch. 4.1 - Given that mA=2x3, and mC=x2+20, find the measure...Ch. 4.1 - Given that mA=2x+y, mB=2x+3y-20, and mC=3x-y+16,...Ch. 4.1 - Assuming that mBmA in , which diagonal AC-orBD-...Ch. 4.1 - Suppose that diagonals AC-andBD- of are drawn and...Ch. 4.1 - In Exercises 17 and 18, consider with VX- RS- and...Ch. 4.1 - In Exercises 17 and 18, consider with VX- RS- and...Ch. 4.1 - In Exercises 19 to 22, classify each statement as...Ch. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Prob. 22ECh. 4.1 - In quadrilateral RSTV, the midpoints of...Ch. 4.1 - In quadrilateral ABCD, the midpoints of opposite...Ch. 4.1 - Quadrilateral ABCD has AB-DC- and AD-BC-. Using...Ch. 4.1 - Quadrilateral RSTV has RS-TV- and RS-TV-. Using...Ch. 4.1 - In Exercises 27-30, use the definition of a...Ch. 4.1 - Prob. 28ECh. 4.1 - In Exercises 27 to 30, use the definition of a...Ch. 4.1 - In Exercises 27-30, use the definition of a...Ch. 4.1 - Prob. 31ECh. 4.1 - In Exercises 31 to 34, write a formal proof of...Ch. 4.1 - Prob. 33ECh. 4.1 - Prob. 34ECh. 4.1 - The bisectors of two consecutive angles of HJKL...Ch. 4.1 - When the bisectors of two consecutive angles of a...Ch. 4.1 - Draw parallelogram RSTV with mR=700 and mS=1100....Ch. 4.1 - Draw parallelogram RSTV so that the diagonals have...Ch. 4.1 - The following problem is based on the...Ch. 4.1 - In the drawing for Exercise 41, the bearing...Ch. 4.1 - Two streets meet to form an obtuse angle at point...Ch. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prove: In a parallelogram, the sum of the squares...Ch. 4.2 - Note: Exercises preceded by an asterisk are of a...Ch. 4.2 - a As shown, must RSTV be a parallelogram? b With...Ch. 4.2 - In the drawing, suppose that WY and XZ bisect each...Ch. 4.2 - In the drawing, suppose that ZX is the...Ch. 4.2 - A carpenter lays out boards of lengths 8 ft, 8 ft,...Ch. 4.2 - A carpenter joins four boards of lengths 6 ft, 6...Ch. 4.2 - In parallelogram ABCD not shown, AB=8, mB=110, and...Ch. 4.2 - In quadrilateral WXYZ, the measures of selected...Ch. 4.2 - In ABC, M and N are midpoints of AC and BC,...Ch. 4.2 - In ABC, M and N are midpoints of AC and BC,...Ch. 4.2 - In Exercises 11 to14 , assume that X, Y , and Z...Ch. 4.2 - Prob. 12ECh. 4.2 - In Exercises 11 to 14, assume that X, Y, and Z are...Ch. 4.2 - Prob. 14ECh. 4.2 - Prob. 15ECh. 4.2 - Prob. 16ECh. 4.2 - For compactness, the drop-down wheels of a...Ch. 4.2 - For compactness, the drop-down legs of an ironing...Ch. 4.2 - In Exercises 19 to 24, complete each proof. Given:...Ch. 4.2 - In Exercises 19 to 24, complete each proof. Given:...Ch. 4.2 - In Exercises 19 to24 , complete each proof. Given:...Ch. 4.2 - In Exercise 19 to24, complete each proof. Given:...Ch. 4.2 - In Exercise 19 to24, complete each proof. Given:...Ch. 4.2 - In Exercise 19 to24, complete each proof. Given:...Ch. 4.2 - Prob. 25ECh. 4.2 - In Exercises 25 to 28, write a formal proof of...Ch. 4.2 - Prob. 27ECh. 4.2 - Prob. 28ECh. 4.2 - In Exercises 29 to 31, M and Nare the midpoints of...Ch. 4.2 - In Exercises 29 to 31, M and Nare the midpoints of...Ch. 4.2 - In Exercises 29 to 31, M and Nare the midpoints of...Ch. 4.2 - Prob. 32ECh. 4.2 - For Exercises 32 to 35, consider kite ABCD with...Ch. 4.2 - For Exercises 32 to 35, consider kite ABCD with...Ch. 4.2 - For Exercises 32 to 35, consider kite ABCD with...Ch. 4.2 - RSTV is a kite, with RSST and RVVT. If mSTV=40,...Ch. 4.2 - In concave kite ABCD, there is an interior angle...Ch. 4.2 - If the length of side AB for kite ABCD is 6 in.,...Ch. 4.2 - Prove that the segment that joins the midpoints of...Ch. 4.2 - Prove that when the midpoints of consecutive sides...Ch. 4.3 - Being as specific as possible, name the type of...Ch. 4.3 - Being as specific as possible, name the type of...Ch. 4.3 - Being as specific as possible, name the type of...Ch. 4.3 - Being as specific as possible, name the type of...Ch. 4.3 - If the diagonals of a parallelogram are...Ch. 4.3 - If the diagonals of a quadrilateral are...Ch. 4.3 - A line segment joins the midpoints of two opposite...Ch. 4.3 - In Exercises 8 to 10, use the properties of...Ch. 4.3 - Prob. 9ECh. 4.3 - In Exercises 8 to 10, use the properties of...Ch. 4.3 - In Exercises 11 to 14, consider MNPQ with...Ch. 4.3 - In Exercises 11 to 14, consider MNPQ with...Ch. 4.3 - In Exercises 11 to 14, consider MNPQ with...Ch. 4.3 - In Exercises 11 to 14, consider MNPQ with...Ch. 4.3 - In Exercises 15 to 18, consider rhombus ABCD with...Ch. 4.3 - In Exercises 15 to 18, consider rhombus ABCD with...Ch. 4.3 - In Exercises 15 to 18, consider rhombus ABCD with...Ch. 4.3 - In Exercises 15 to 18, consider rhombus ABCD with...Ch. 4.3 - Given: ABCD not shown with AB = 8 and BC = 6; M...Ch. 4.3 - Given: Rhombus RSTV not shown with diagonals...Ch. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Which types of quadrilaterals is are necessarily...Ch. 4.3 - Find the perimeter of the cyclic quadrilateral...Ch. 4.3 - Find the perimeter of the square shown.Ch. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Prob. 31ECh. 4.3 - Prob. 32ECh. 4.3 - Prob. 33ECh. 4.3 - Prob. 34ECh. 4.3 - Prob. 35ECh. 4.3 - Prob. 36ECh. 4.3 - In Exercises 32 to 37, write a formal proof of...Ch. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - a Argue that the midpoint of the hypotenuse of a...Ch. 4.3 - Two sets of rails railroad tracks are equally...Ch. 4.3 - In square ABCD not shown, point E lies on side DC....Ch. 4.3 - In square ABCD not shown, point E lies in the...Ch. 4.3 - The sides of square ABCD are trisected at the...Ch. 4.4 - Find the measures of the remaining angles of...Ch. 4.4 - Find the measures of the remaining angles of...Ch. 4.4 - What type of trapezoid a has congruent diagonals....Ch. 4.4 - What type quadrilateral is formed when the...Ch. 4.4 - Given isosceles trapezoid ABCD, Find. a AC, if BD...Ch. 4.4 - In trapezoid ABCD, MN is the median. Without...Ch. 4.4 - If HandJ are supplementary, what type of...Ch. 4.4 - If HandJ are supplementary in HJKL, are KandL...Ch. 4.4 - For Exercises 9 and 10, consider isosceles...Ch. 4.4 - For Exercises 9 and 10, consider isosceles...Ch. 4.4 - In Exercises 11 to 16, the drawing shows trapezoid...Ch. 4.4 - In Exercises 11 to 16, the drawing shows trapezoid...Ch. 4.4 - In Exercises 11 to 16, the drawing shows trapezoid...Ch. 4.4 - In Exercises 11 to 16, the drawing shows trapezoid...Ch. 4.4 - In Exercises 11 to 16, the drawing shows trapezoid...Ch. 4.4 - In Exercises 11 to 16, the drawing shows trapezoid...Ch. 4.4 - Given: ABCD is an isosceles trapezoid. Prove: ABE...Ch. 4.4 - Given: Isosceles ABE with AEBE; also, D and C are...Ch. 4.4 - In isosceles trapezoid WXYZ with bases ZY and WX,...Ch. 4.4 - In trapezoid WXYZ with bases ZY and WX, ZY = 12,...Ch. 4.4 - In isosceles trapezoid MNPQ with MNQP, diagonal...Ch. 4.4 - In trapezoid RSTV, RVST,mSRV=90, and M and N are...Ch. 4.4 - Each vertical section of a suspension bridge is in...Ch. 4.4 - The state of Nevada approximates the shape of a...Ch. 4.4 - In the figure, abc and B is the midpoint of AC. If...Ch. 4.4 - In the figure, abc and B is the midpoint of AC. If...Ch. 4.4 - Prob. 27ECh. 4.4 - In exercises 27 to 33, complete a formal proof....Ch. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - In exercises 27 to 33, complete a formal proof. If...Ch. 4.4 - Prob. 32ECh. 4.4 - In exercises 27 to 33, complete a formal proof....Ch. 4.4 - Prob. 34ECh. 4.4 - For exercises 34 and 35, EFis the median of...Ch. 4.4 - Given: ABDC mA=mB=56CEDA and CF bisects DCB Find:...Ch. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - The vertical side wall of an in-ground pool that...Ch. 4.4 - Prob. 40ECh. 4.4 - With MNQP and MQQP, MNPQ is a right trapezoid....Ch. 4.4 - With MNQP and MQ, MNPQ is a right trapezoid. Find...Ch. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Draw and then trisect AB. Use the construction...Ch. 4.CR - Review Exercises State whether the statements in...Ch. 4.CR - Prob. 2CRCh. 4.CR - Prob. 3CRCh. 4.CR - Prob. 4CRCh. 4.CR - Prob. 5CRCh. 4.CR - Prob. 6CRCh. 4.CR - Prob. 7CRCh. 4.CR - Review Exercises State whether the statements in...Ch. 4.CR - Prob. 9CRCh. 4.CR - Prob. 10CRCh. 4.CR - Prob. 11CRCh. 4.CR - Prob. 12CRCh. 4.CR - Review Exercises Given: ABCD CD=2x+3 BC=5x-4...Ch. 4.CR - Review Exercises Given: ABCD mA=2x+6 mB=x+24 Find:...Ch. 4.CR - Review Exercises The diagonals of ABCD not shown...Ch. 4.CR - Review Exercises Given: MNOP mM=4x mO=2x+50 Find:...Ch. 4.CR - Review Exercises Using the information from Review...Ch. 4.CR - Review Exercises In quadrilateral ABCD, M is the...Ch. 4.CR - Review Exercises In isosceles trapezoid DEFG,...Ch. 4.CR - One base of a trapezoid has a length of 12.3 cm...Ch. 4.CR - Review Exercises In trapezoid MNOP, MN-PO- and R...Ch. 4.CR - Review Exercises In Review Exercises 22 to 24, M...Ch. 4.CR - Review Exercises In Review Exercises 22 to 24, M...Ch. 4.CR - Review Exercises In Review Exercises 22 to 24, M...Ch. 4.CR - Review Exercises Given: ABCD is a AF-CE- Prove:...Ch. 4.CR - Review Exercises Given: ABEF is a rectangle BCDE...Ch. 4.CR - Prob. 27CRCh. 4.CR - Prob. 28CRCh. 4.CR - Review Exercises Given: ABCD is a parallelogram...Ch. 4.CR - Review Exercises Given: TWX is an isosceles, with...Ch. 4.CR - Prob. 31CRCh. 4.CR - Review Exercises Draw rectangle ABCD with AB=5 and...Ch. 4.CR - Review Exercises Draw rectangle WXYZ with...Ch. 4.CR - Prob. 34CRCh. 4.CR - Review Exercises What type of quadrilateral is...Ch. 4.CT - Consider ABCD as shown. a How are A and C...Ch. 4.CT - In RSTV not shown, RS=5.3 cm and ST=4.1 cm. Find...Ch. 4.CT - Prob. 3CTCh. 4.CT - Prob. 4CTCh. 4.CT - Prob. 5CTCh. 4.CT - Complete each statement: a If a quadrilateral has...Ch. 4.CT - Prob. 7CTCh. 4.CT - Prob. 8CTCh. 4.CT - Prob. 9CTCh. 4.CT - In ABC, M is the midpoint of AB and N is the...Ch. 4.CT - In rectangle ABCD, AD=12 and DC=5. Find the length...Ch. 4.CT - In trapezoid RSTV, RSVT. a Which sides are the...Ch. 4.CT - In trapezoid RSTV, RSVT and MN is the median, Find...Ch. 4.CT - In trapezoid RSTV of Exercise 13, RSVT and MN is...Ch. 4.CT - Complete the proof of the following theorem: In a...Ch. 4.CT - Complete the proof of the following theorem: The...Ch. 4.CT - In Kite RSTV, RS=2x4,ST=x1,TV=y3andRV=y. Find the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Let D be a directed graph, with loops allowed, for which the indegree at each vertex is at most k and the outdegree at each vertex is at most k. Prove that the arcs of D can be colored so that the arcs entering each vertex must have distinct colors and the arcs leaving each vertex have distinct colors. An arc entering a vertex may have the same color as an arc leaving it. It is probably easiest to make use of a known result about edge coloring. Think about splitting each vertex into an ‘in’ and ‘out’ part and consider what type of graph you get.arrow_forward10 20 30 y vernier protractor scales. 60 30 0 30 60 40 30 20 10 0 30 60 0 10. Write the complement of each of the following angles. a. 67° b. 17°41' 11. Write the supplement of each of the following angles. a.41° b.99°32' 30 60 C. 20 10 20 90 60 30 69 30 30 40 50 c. 54°47' 53" 0 30 60 c. 103°03'27" 12. Given: AB CD and EF GH. Determine the value of each angle, 21 through /10, to the nearer minute. A- 25 21 = 22 = 23 = 24 = 25 = 46= 27 = C 28 = 29 = 210 = E 26 22 210 81°00' 29 4 142°00' G H 94°40' B Darrow_forwardName: Tan Tong 16.5 Bonvicino - Period 5 1 Find the exact volume of a right hexagonal prism such that the base is a regular hexagon with a side length of 8 cm and whose distance between the two bases is 5 cm. Show all work. (4 pts) 83 tan 30°= Regular hexagon So length ~ 480 tango Cm Hexagon int angle =36016 8cm Angle bisec isper p bisect Side length 4 X=an 300 2 In the accompanying diagram of circle O, PA is tangent to the circle at A, PDC is a secant, diameter AEOC intersects chord BD at E, chords AB, BC, and DA are drawn, mDA = 46° and mBC is 32° more than mAB. If the radius of the circle is 8 cm, E is the midpoint of AO and the length of ED is 2 less than the length of BE, answer each of the following. Show all work. (a) marrow_forward18:36 G.C.A.2.ChordsSecantsandTa... จ 76 完成 2 In the accompanying diagram, AABC is inscribed in circle O, AP bisects BAC, PBD is tangent to circle O at B, and mZACB:m/CAB:m/ABC= 4:3:2 D B P F Find: mZABC, mBF, m/BEP, m/P, m/PBC ← 1 Őarrow_forward14:09 2/16 jmap.org 5G 66 In the accompanying diagram of circle O, diameters BD and AE, secants PAB and PDC, and chords BC and AD are drawn; mAD = 40; and mDC = 80. B E Find: mAB, m/BCD, m/BOE, m/P, m/PAD ← G.C.A.2.ChordsSecantsand Tangent s19.pdf (538 KB) + 4 保存... Xarrow_forward16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forwardAnswer question 4 pleasearrow_forward16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forwardAnswer question 3 pleasearrow_forwardAnswer question 3 pleasearrow_forward38 Below triangle is isosceles. Find the value of x. 70° 60° x 20° Warrow_forwardTo approximate the length of a marsh, a surveyor walks x = 400 meters from point A to point B. Then, the surveyor turns 75° and walks 220 meters to point C (see figure). Approximate the length AC of the marsh. (Round your answer to one decimal place.) m C B 75° 220 m x marrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY