
a.
To graph: showing the height with respect to time.
a.
Explanation of Solution
Given:
A person starts swinging from the ground, then attains a maximum height and then slows down until the swing stops.
Concept used:
Given example is of a damped oscillation where the swing is oscillating between its amplitude and due to damping force, its amplitude is continuously decreasing.
For a simple oscillation without damping the equation is
But as stated the height of the swing will first increase meaning that the amplitude will increase and then decrease, thus there will be 2 parts of the graph, one with increasing amplitude and one with decreasing amplitude.
The equation of graph for the part when swing starts from the ground and increases its amplitude will be
Here it must be noted that the power of eand value of
Thus the graph formed is given below.
Graph:
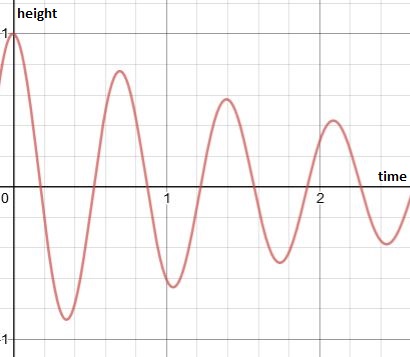
Interpretation:
The height of the swing gradually increases from 0 up to maximum height while passing through the mean position every time.
Here height at 0 doesn’t mean ground level but the mean height from the ground
Now, for the second part of the graph where the height of the swing decreases gradually until it stop, the equation will have cosine function as it starts from maximum value and ends at 0
So the equation for this graph will be
Conclusion:
The height of swing will decrease gradually because of the damped forces acting such as friction. Eventually the height becomes zero and the swing stops.
b.
To find: the change in the graph if instead of slowing down the person jumps from the swing.
b.
Answer to Problem 3P
A parabola will be formed
Explanation of Solution
Given:
A person is swingfrom any point from him, and jumps to land on the ground.
Concept used:
When the person is swinging, he already has some momentum because of the motion of the swing.
If he jumps from the swing at any point he will follow a parabolic path because of his velocity in horizontal direction and due to the gravitational force in vertical direction
Due to the momentum the person will be launched into air from the swing and he will follow a parabolic path.
Graph:
The 1st part of graph will be similar as there are no changes while speeding up but the second part of graph will be different as given below.
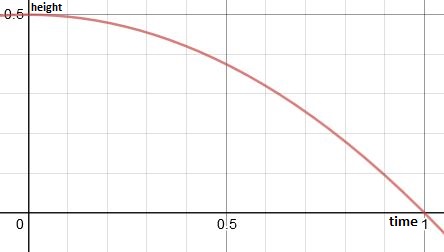
Conclusion:
If the person jumps from the swing mid-air instead of slowing down, he follows a trajectory of a parabola.
Chapter 4 Solutions
High School Math 2015 Common Core Algebra 1 Student Edition Grade 8/9
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
College Algebra with Modeling & Visualization (5th Edition)
Thinking Mathematically (6th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- In simplest terms, Sketch the graph of the parabola. Then, determine its equation. opens downward, vertex is (- 4, 7), passes through point (0, - 39)arrow_forwardIn simplest way, For each quadratic relation, find the zeros and the maximum or minimum. a) y = x 2 + 16 x + 39 b) y = 5 x2 - 50 x - 120arrow_forwardIn simplest terms and step by step Write each quadratic relation in standard form, then fi nd the zeros. y = - 4( x + 6)2 + 36arrow_forward
- In simplest terms and step by step For each quadratic relation, find the zeros and the maximum or minimum. 1) y = - 2 x2 - 28 x + 64 2) y = 6 x2 + 36 x - 42arrow_forwardWrite each relation in standard form a)y = 5(x + 10)2 + 7 b)y = 9(x - 8)2 - 4arrow_forwardIn simplest form and step by step Write the quadratic relation in standard form, then fi nd the zeros. y = 3(x - 1)2 - 147arrow_forward
- Step by step instructions The path of a soccer ball can be modelled by the relation h = - 0.1 d 2 + 0.5 d + 0.6, where h is the ball’s height and d is the horizontal distance from the kicker. a) Find the zeros of the relation.arrow_forwardIn simplest terms and step by step how do you find the zeros of y = 6x2 + 24x - 192arrow_forwardStep by step Find the zeros of each quadratic relation. a) y = x2 - 16xarrow_forward
- In simplest step by step terms, how do you find the zeros of y = x2 - 16arrow_forwardIn simplest terms, Describe the shape and position of the parabola relative to the graph of y = x 2 y = - 80( x + 9) 2 + 10.8arrow_forwardas a Identify each equation Parabola, circle, ellipse perbola without completio the square. x²-6x-14 y = 33-y² 14y ofarrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





