Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
5th Edition
ISBN: 9781323132098
Author: Thomas, Lay
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 4.1, Problem 19E
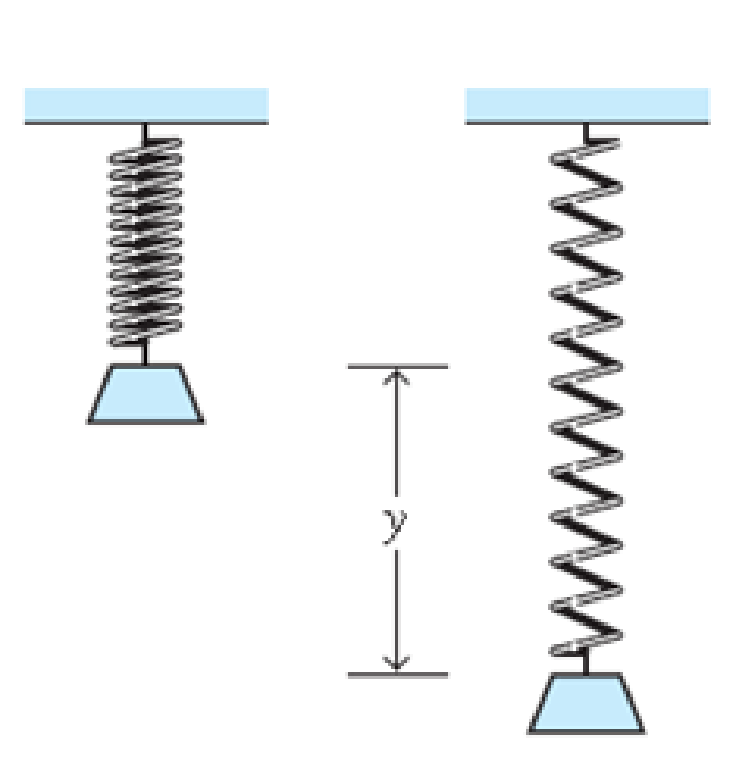
If a mass m is placed at the end of a spring, and if the mass is pulled downward and released, the mass-spring system will begin to oscillate. The displacement y of the mass from its resting position is given by a function of the form
y(t) = c1 cosωt + c2 cosωt (5)
where ω is a constant that depend s on the spring and the mass. (See the figure below.) Show that the set of all functions described in (5) (with ω fixed and c1, c2 arbitrary) is a
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule03:03
Chapter 4 Solutions
Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
Ch. 4.1 - Show that the set H of all points in 2 of the form...Ch. 4.1 - Let W = Span{v1,...,vp}, where v1,..,vp are in a...Ch. 4.1 - An n n matrix A is said to be symmetric if AT =...Ch. 4.1 - Let V be the first quadrant in the xy-plane; that...Ch. 4.1 - Let W be the union of the first and third...Ch. 4.1 - Let H be the set of points inside and on the unit...Ch. 4.1 - Construct a geometric figure that illustrates why...Ch. 4.1 - In Exercises 58, determine if the given set is a...Ch. 4.1 - In Exercises 58, determine if the given set is a...Ch. 4.1 - In Exercises 58, determine if the given set is a...
Ch. 4.1 - In Exercises 58, determine if the given set is a...Ch. 4.1 - Let H be the set of all vectors of the form...Ch. 4.1 - Let H be the set of all vectors of the form...Ch. 4.1 - Let W be the set of all vectors of the form...Ch. 4.1 - Let W be the set of all vectors of the form...Ch. 4.1 - Let v1 = [101], v2 = [213], v3 = [426], and w=...Ch. 4.1 - Let v1, v2, v3 be as in Exercise 13, and let w =...Ch. 4.1 - In Exercises 1518, let W be the set of all vectors...Ch. 4.1 - In Exercises 1518, let W be the set of all vectors...Ch. 4.1 - In Exercises 1518, let W be the set of all vectors...Ch. 4.1 - In Exercises 1518, let W be the set of all vectors...Ch. 4.1 - If a mass m is placed at the end of a spring, and...Ch. 4.1 - The set of all continuous real-valued functions...Ch. 4.1 - Determine if the set H of all matrices of the form...Ch. 4.1 - Let F be a fixed 32 matrix, and let H be the set...Ch. 4.1 - In Exercises 23 and 24, mark each statement True...Ch. 4.1 - a. A vector is any element of a vector space. b....Ch. 4.1 - Exercises 2529 show how the axioms for a vector...Ch. 4.1 - Exercises 2529 show how the axioms for a vector...Ch. 4.1 - Exercises 2529 show how the axioms for a vector...Ch. 4.1 - Exercises 2529 show how the axioms for a vector...Ch. 4.1 - Exercises 2529 show how the axioms for a vector...Ch. 4.1 - Suppose cu = 0 for some nonzero scalar c. Show...Ch. 4.1 - Let u and v be vectors in a vector space V, and...Ch. 4.1 - Let H and K be sub spaces of a vector space V. The...Ch. 4.1 - Given subspaces H and K of a vector space V, the...Ch. 4.1 - Suppose u1,..., up and v1,..., vq are vectors in a...Ch. 4.1 - [M] Show that w is in the subspace of 4 spanned by...Ch. 4.1 - [M] Determine if y is in the subspace of 4 spanned...Ch. 4.1 - [M] The vector space H = Span {1, cos2t, cos4t,...Ch. 4.1 - Prob. 38ECh. 4.2 - Let W = {[abc]:a3bc=0}. Show in two different ways...Ch. 4.2 - Let A = [735415524], v = [211], and w = [763]....Ch. 4.2 - Let A be an n n matrix. If Col A = Nul A, show...Ch. 4.2 - Determine if w = [134] is in Nul A, where A =...Ch. 4.2 - Determine if w = [532] is in Nul A, where A =...Ch. 4.2 - In Exercises 36, find an explicit description of...Ch. 4.2 - In Exercises 36, find an explicit description of...Ch. 4.2 - In Exercises 36, find an explicit description of...Ch. 4.2 - In Exercises 36, find an explicit description of...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 714, either use an appropriate...Ch. 4.2 - In Exercises 15 and 16, find A such that the given...Ch. 4.2 - Prob. 16ECh. 4.2 - For the matrices in Exercises 1720, (a) find k...Ch. 4.2 - For the matrices in Exercises 1720, (a) find k...Ch. 4.2 - For the matrices in Exercises 1720, (a) find k...Ch. 4.2 - For the matrices in Exercises 17-20, (a) find k...Ch. 4.2 - With A as in Exercise 17, find a nonzero vector in...Ch. 4.2 - With A as in Exercise 3, find a nonzero vector in...Ch. 4.2 - Let A=[61236] and w=[21]. Determine if w is in Col...Ch. 4.2 - Let A=[829648404] and w=[212]. Determine w is in...Ch. 4.2 - In Exercises 25 and 26, A denotes an m n matrix....Ch. 4.2 - In Exercises 25 and 26, A denotes an m n matrix....Ch. 4.2 - It can be shown that a solution of the system...Ch. 4.2 - Consider the following two systems of equations:...Ch. 4.2 - Prove Theorem 3 as follows: Given an m n matrix...Ch. 4.2 - Let T : V W be a linear transformation from a...Ch. 4.2 - Define T : p2 by T(p)=[p(0)p(1)]. For instance, if...Ch. 4.2 - Define a linear transformation T: p2 2 by...Ch. 4.2 - Let M22 be the vector space of all 2 2 matrices,...Ch. 4.2 - (Calculus required) Define T : C[0, 1 ] C[0, 1]...Ch. 4.2 - Let V and W be vector spaces, and let T : V W be...Ch. 4.2 - Given T : V W as in Exercise 35, and given a...Ch. 4.2 - [M] Determine whether w is in the column space of...Ch. 4.2 - [M] Determine whether w is in the column space of...Ch. 4.2 - [M] Let a1,,a5 denote the columns of the matrix A,...Ch. 4.2 - [M] Let H = Span {v1, v2} and K = Span {v3, v4},...Ch. 4.3 - Let v1=[123] and v2=[279]. Determine if {v1, v2}...Ch. 4.3 - Let v1=[134], v2=[621], v3=[223], and v4=[489]....Ch. 4.3 - Let v1=[100], v2=[010], and H={[ss0]:sin}. Then...Ch. 4.3 - Let V and W be vector spaces, let T : V W and U :...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Determine which sets in Exercises 1-8 are bases...Ch. 4.3 - Find bases for the null spaces of the matrices...Ch. 4.3 - Find bases for the null spaces of the matrices...Ch. 4.3 - Find a basis for the set of vectors in 3 in the...Ch. 4.3 - Find a basis for the set of vectors in 2 on the...Ch. 4.3 - In Exercises 13 and 14, assume that A is row...Ch. 4.3 - In Exercises 13 and 14, assume that A is row...Ch. 4.3 - In Exercises 15-18, find a basis for the space...Ch. 4.3 - In Exercises 15-18, find a basis for the space...Ch. 4.3 - In Exercises 15-18, find a basis for the space...Ch. 4.3 - In Exercises 15-18, find a basis for the space...Ch. 4.3 - Let v1=[437], v2=[192], v3=[7116], and H =...Ch. 4.3 - Let v1=[7495], v2=[4725], v3=[1534]. It can be...Ch. 4.3 - In Exercises 21 and 22, mark each statement True...Ch. 4.3 - In Exercises 21 and 22, mark each statement True...Ch. 4.3 - Suppose 4 = Span {v1,,v4}. Explain why {v1,,v4} is...Ch. 4.3 - Let B = {v1,..., vn} be a linearly independent set...Ch. 4.3 - Let v1=[101], v2=[011], v3=[010], and let H be the...Ch. 4.3 - In the vector space of all real-valued functions,...Ch. 4.3 - Let V be the vector space of functions that...Ch. 4.3 - (RLC circuit) The circuit in the figure consists...Ch. 4.3 - Exercises 29 and 30 show that every basis for n...Ch. 4.3 - Exercises 29 and 30 show that every basis for n...Ch. 4.3 - Exercises 31 and 32 reveal an important connection...Ch. 4.3 - Exercises 31 and 32 reveal an important connection...Ch. 4.3 - Consider the polynomials p1(t) = 1 + t2 and p2(t)...Ch. 4.3 - Consider the polynomials p1(t) = 1 + t, p2(t) = 1 ...Ch. 4.3 - Let V be a vector space that contains a linearly...Ch. 4.3 - [M] Let H = Span {u1, u2, u3} and K = Span{v1,v2,...Ch. 4.3 - [M] Show that {t, sin t, cos 2t, sin t cos t} is a...Ch. 4.3 - [M] Show that {1, cos t, cos2 t,..., cos6t} is a...Ch. 4.4 - Let b1=[100], b2=[340], b3=[363], and x=[823]. a....Ch. 4.4 - The set B = {1 + t, 1 + t2, t + t2} is a basis for...Ch. 4.4 - In Exercises 1-4, find the vector x determined by...Ch. 4.4 - In Exercises 1-4, find the vector x determined by...Ch. 4.4 - In Exercises 1-4, find the vector x determined by...Ch. 4.4 - In Exercises 1-4, find the vector x determined by...Ch. 4.4 - In Exercises 5-8, find the coordinate vector [ x...Ch. 4.4 - In Exercises 5-8, find the coordinate vector [ x...Ch. 4.4 - In Exercises 5-8, find the coordinate vector [ x...Ch. 4.4 - In Exercises 5-8, find the coordinate vector [ x...Ch. 4.4 - In Exercises 9 and 10, find the...Ch. 4.4 - In Exercises 9 and 10, find the...Ch. 4.4 - In Exercises 11 and 12, use an inverse matrix to...Ch. 4.4 - In Exercises 11 and 12, use an inverse matrix to...Ch. 4.4 - The set B = {1 + t2, t + t2, 1 + 2t + t2} is a...Ch. 4.4 - The set B = {1 t2, t t2, 2 2t + t2} is a basis...Ch. 4.4 - In Exercises 15 and 16, mark each statement True...Ch. 4.4 - In Exercises 15 and 16, mark each statement True...Ch. 4.4 - The vectors v1=[13], v2=[28], v3=[37] span 2 but...Ch. 4.4 - Let B = {b1,...,bn} be a basis for a vector space...Ch. 4.4 - Let S be a finite set in a vector space V with the...Ch. 4.4 - Suppose {v1,...,v4} is a linearly dependent...Ch. 4.4 - Let B={[14],[29]}. Since the coordinate mapping...Ch. 4.4 - Let B = {b1,...,bn} be a basis for n. Produce a...Ch. 4.4 - Exercises 23-26 concern a vector space V, a basis...Ch. 4.4 - Exercises 23-26 concern a vector space V, a basis...Ch. 4.4 - Exercises 23-26 concern a vector space V, a basis...Ch. 4.4 - Exercises 23-26 concern a vector space V, a basis...Ch. 4.4 - In Exercises 27-30, use coordinate vectors to test...Ch. 4.4 - In Exercises 27-30, use coordinate vectors to test...Ch. 4.4 - In Exercises 27-30, use coordinate vectors to test...Ch. 4.4 - In Exercises 27-30, use coordinate vectors to test...Ch. 4.4 - Use coordinate vectors to test whether the...Ch. 4.4 - Let p1 (t) = 1 + t2, p2(t) = t 3t2, p3 (t) = 1 +...Ch. 4.4 - In Exercises 33 and 34, determine whether the sets...Ch. 4.4 - In Exercises 33 and 34, determine whether the sets...Ch. 4.4 - Prob. 35ECh. 4.4 - [M] Let H = Span{v1,v2, v3} and B ={v1,v2, v3}....Ch. 4.4 - [M] Exercises 37 and 38 concern the crystal...Ch. 4.4 - [M] Exercises 37 and 38 concern the crystal...Ch. 4.5 - Decide whether each statement is True or False,...Ch. 4.5 - Let H and K be subspaces of a vector space V. In...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - For each subspace in Exercises 1-8, (a) find a...Ch. 4.5 - Find the dimension of the subspace of all vectors...Ch. 4.5 - Find the dimension of the subspace H of 2 spanned...Ch. 4.5 - In Exercises 11 and 12, find the dimension of the...Ch. 4.5 - In Exercises 11 and 12, find the dimension of the...Ch. 4.5 - Determine the dimensions of Nul A and Col A for...Ch. 4.5 - Determine the dimensions of Nul A and Col A for...Ch. 4.5 - Determine the dimensions of Nul A and Col A for...Ch. 4.5 - Determine the dimensions of Nul A and Col A for...Ch. 4.5 - Determine the dimensions of Nul A and Col A for...Ch. 4.5 - In Exercises 19 and 20, V is a vector space. Mark...Ch. 4.5 - In Exercises 19 and 20, V is a vector space. Mark...Ch. 4.5 - The first four Hermite polynomials are 1, 2t, 2 +...Ch. 4.5 - The first four Laguerre polynomials are 1, 1 t, 2...Ch. 4.5 - Let B be the basis of 3 consisting of the Hermite...Ch. 4.5 - Let B be the basis of 2 consisting of the first...Ch. 4.5 - Let S be a subset of an n-dimensional vector space...Ch. 4.5 - Let H be an n-dimensional subspace of an...Ch. 4.5 - Explain why the space of all polynomials is an...Ch. 4.5 - Show that the space C() of all continuous...Ch. 4.5 - In Exercises 29 and 30, V is a nonzero...Ch. 4.5 - In Exercises 29 and 30, V is a nonzero...Ch. 4.5 - Exercises 31 and 32 concern finite-dimensional...Ch. 4.5 - Exercises 31 and 32 concern finite-dimensional...Ch. 4.6 - The matrices below are row equivalent....Ch. 4.6 - The matrices below are equivalent....Ch. 4.6 - The matrices below are row equivalent....Ch. 4.6 - The matrices below are equivalent....Ch. 4.6 - In Exercises 1-4, assume that the matrix A is row...Ch. 4.6 - In Exercises 1-4, assume that the matrix A is row...Ch. 4.6 - In Exercises 1-4, assume that the matrix A is row...Ch. 4.6 - In Exercises 1-4, assume that the matrix A is row...Ch. 4.6 - If a 3 8 matrix A has rank 3, find dim Nul A, dim...Ch. 4.6 - If a 6 3 matrix A has rank 3, find dim Nul A, dim...Ch. 4.6 - Suppose a 4 7 matrix A has four pivot columns. Is...Ch. 4.6 - Suppose a 5 6 matrix A has four pivot columns....Ch. 4.6 - If the null space of a 5 6 matrix A is...Ch. 4.6 - If the null space of a 7 6 matrix A is...Ch. 4.6 - If the null space of an 8 5 matrix A is...Ch. 4.6 - If the null space of a 5 6 matrix A is...Ch. 4.6 - If A is a 7 5 matrix, what is the largest...Ch. 4.6 - If A is a 4 3 matrix, what is the largest...Ch. 4.6 - If A is a 6 8 matrix, what is the smallest...Ch. 4.6 - If A is a 6 4 matrix, what is the smallest...Ch. 4.6 - In Exercises 17 and 18, A is an m n matrix. Mark...Ch. 4.6 - In Exercises 17 and 18, A is an m n matrix. Mark...Ch. 4.6 - Suppose the solutions of a homogeneous system of...Ch. 4.6 - Suppose a nonhomogeneous system of six linear...Ch. 4.6 - Suppose a nonhomogeneous system of nine linear...Ch. 4.6 - Is it possible that all solutions of a homogeneous...Ch. 4.6 - A homogeneous system of twelve linear equations in...Ch. 4.6 - Is it possible for a nonhomogeneous system of...Ch. 4.6 - A scientist solves a nonhomogeneous system of ten...Ch. 4.6 - In statistical theory, a common requirement is...Ch. 4.6 - Exercises 27-29 concern an m n matrix A and what...Ch. 4.6 - Exercises 27-29 concern an m n matrix A and what...Ch. 4.6 - Exercises 27-29 concern an m n matrix A and what...Ch. 4.6 - Prob. 30ECh. 4.6 - Rank 1 matrices are important in some computer...Ch. 4.6 - Rank 1 matrices are important in some computer...Ch. 4.6 - Rank 1 matrices are important in some computer...Ch. 4.7 - Let B = {b1, b2} and C = {c1, c2} be bases for a...Ch. 4.7 - Let B = {b1, b2} and C = {c1, c2} be bases for a...Ch. 4.7 - Let u = {u1, u2} and w = {w1, w2} be bases for V,...Ch. 4.7 - Let A = {a1, a2, a3} and D = {d1, d2, d3} be bases...Ch. 4.7 - Let A = {a1, a2, a3} and B = {b1, b2, b3} be bases...Ch. 4.7 - Let D = {d1, d2, d3} and F = {f1, f2, f3} be bases...Ch. 4.7 - In Exercises 7-10, let B = {b1, b2} and C = {c1,...Ch. 4.7 - In Exercises 7-10, let B = {b1, b2} and C = {c1,...Ch. 4.7 - In Exercises 7-10, let B = {b1, b2} and C = {c1,...Ch. 4.7 - In Exercises 7-10, let B = {b1, b2} and C = {c1,...Ch. 4.7 - In Exercises 11 and 12, B and C are bases for a...Ch. 4.7 - In Exercises 11 and 12, B and C are bases for a...Ch. 4.7 - In 2 find the change-of-coordinates matrix from...Ch. 4.7 - In 2 find the change-of-coordinates matrix from...Ch. 4.7 - Exercises 15 and 16 provide a proof of Theorem 15....Ch. 4.7 - Prob. 16ECh. 4.7 - Prob. 17ECh. 4.7 - Prob. 18ECh. 4.7 - [M] Let P=[121350461],v1=[223],v2=[852],v3=[726]...Ch. 4.7 - Let B = {b1, b2}, C = {c1, c2}, and D = {d1, d2}...Ch. 4.8 - Verify that the signals in Exercises 1 and 2 are...Ch. 4.8 - Prob. 2ECh. 4.8 - Prob. 3ECh. 4.8 - Show that the signals in Exercises 3-6 form a...Ch. 4.8 - Show that the signals in Exercises 3-6 form a...Ch. 4.8 - Show that the signals in Exercises 3-6 form a...Ch. 4.8 - Prob. 7ECh. 4.8 - Prob. 8ECh. 4.8 - Prob. 9ECh. 4.8 - Prob. 10ECh. 4.8 - Prob. 11ECh. 4.8 - Prob. 12ECh. 4.8 - In Exercises 13-16, find a basis for the solution...Ch. 4.8 - In Exercises 13-16, find a basis for the solution...Ch. 4.8 - In Exercises 13-16, find a basis for the solution...Ch. 4.8 - In Exercises 13-16, find a basis for the solution...Ch. 4.8 - Exercises 17 and 18 concern a simple model of the...Ch. 4.8 - Exercises 17 and 18 concern a simple model of the...Ch. 4.8 - Prob. 19ECh. 4.8 - A lightweight cantilevered beam is supported at N...Ch. 4.8 - Prob. 23ECh. 4.8 - Prob. 24ECh. 4.8 - Prob. 25ECh. 4.8 - Prob. 26ECh. 4.8 - Prob. 27ECh. 4.8 - Prob. 28ECh. 4.8 - Prob. 29ECh. 4.8 - Write the difference equations in Exercises 29 and...Ch. 4.8 - Prob. 31ECh. 4.8 - Prob. 32ECh. 4.8 - Let yk = k2 and zk = 2k|k|. Are the signals {yk}...Ch. 4.8 - Let f, g, and h be linearly independent functions...Ch. 4.8 - Prob. 35ECh. 4.8 - Prob. 37ECh. 4.9 - Suppose the residents of a metropolitan region...Ch. 4.9 - Prob. 2PPCh. 4.9 - Prob. 3PPCh. 4.9 - A small remote village receives radio broadcasts...Ch. 4.9 - A laboratory animal may cat any one of three foods...Ch. 4.9 - On any given day, a student is either healthy or...Ch. 4.9 - The weather in Columbus is either good,...Ch. 4.9 - In Exercises 5-8, find the steady-state vector. 5....Ch. 4.9 - In Exercises 5-8, find the steady-state vector. 6....Ch. 4.9 - In Exercises 5-8, find the steady-state vector. 7....Ch. 4.9 - In Exercises 5-8, find the steady-state vector. 8....Ch. 4.9 - Determine if p=[.21.80] is a regular stochastic...Ch. 4.9 - Determine if p=[1.20.8] is a regular stochastic...Ch. 4.9 - a. Find the steady-state vector for the Markov...Ch. 4.9 - Refer to Exercise 2. Which food will the animal...Ch. 4.9 - a. Find the steady-state vector for the Markov...Ch. 4.9 - Refer to Exercise 4. In the long run, how likely...Ch. 4.9 - Let P be an n n stochastic matrix. The following...Ch. 4.9 - Show that every 2 2 stochastic matrix has at...Ch. 4.9 - Let S be the 1 n row matrix with a 1 in each...Ch. 4.9 - Prob. 20ECh. 4 - Mark each statement True or False. Justify each...Ch. 4 - Find a basis for the set of all vectors of the...Ch. 4 - Let u1=[246], u2=[125], b=[b1b2b3], and W =...Ch. 4 - Explain what is wrong with the following...Ch. 4 - Consider the polynomials p1(t) = 1 +t, p2(t) = 1 ...Ch. 4 - Prob. 6SECh. 4 - Prob. 7SECh. 4 - Prob. 8SECh. 4 - Let T : n m be a linear transformation. a. What...Ch. 4 - Prob. 10SECh. 4 - Let S be a finite minimal spanning set of a vector...Ch. 4 - Prob. 12SECh. 4 - Exercises 12-17 develop properties of rank that...Ch. 4 - Prob. 14SECh. 4 - Prob. 15SECh. 4 - Exercises 12-17 develop properties of rank that...Ch. 4 - Exercises 12-17 develop properties of rank that...Ch. 4 - The concept of rank plays an important role in the...Ch. 4 - Determine if the matrix pairs in Exercises 19-22...Ch. 4 - Determine if the matrix pairs in Exercises 19-22...Ch. 4 - Determine if the matrix pairs in Exercises 19-22...Ch. 4 - Prob. 22SE
Additional Math Textbook Solutions
Find more solutions based on key concepts
In each of Exercises 21–30, draw a linear graph to represent the given information. Be sure to label and number...
Elementary Algebra: Concepts and Applications (10th Edition)
In Exercises 1 and 2, determine if the function f defined by the arrow diagram has an inverse. If it does, crea...
College Algebra in Context with Applications for the Managerial, Life, and Social Sciences (5th Edition)
Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...
Algebra and Trigonometry (6th Edition)
NOTE: Write your answers using interval notation when appropriate.
CHECKING ANALYTIC SKILLS Fill in each blank ...
A Graphical Approach to College Algebra (6th Edition)
Decide whether the matrices in Exercises 1 through 15 are invertible. If they are, find the inverse. Do the com...
Linear Algebra with Applications (2-Download)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY