EBK ESSENTIAL UNIVERSITY PHYSICS, VOLUM
4th Edition
ISBN: 9780135272992
Author: Wolfson
Publisher: VST
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 4, Problem 79PP
Laptop computers are equipped with accelerometers that sense when the device is dropped and then put the hard drive into a protective mode. Your computer geek friend has written a program that reads the accelerometer and calculates the laptop’s apparent weight. You’re amusing yourself with this program on a long plane flight. Your laptop weighs just 5 pounds, and for a long time that’s what the program reports. But then the “Fasten Seatbelt” light comes on as the plane encounters turbulence. For the next 12 seconds, your laptop reports rapid changes in apparent weight, as shown in Fig. 4.29.
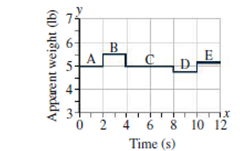
FIGURE 4.29 The laptop’s apparent weight (Passage Problems 76-79).
The magnitude of the greatest vertical acceleration the plane undergoes during the time shown on the graph is approximately
- a. 0.5 m/s2.
- b. 1 m/s2.
- c. 5 m/s2.
- d. 10 m/s2.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Ammonia enters the compressor of an industrial refrigeration plant at 2 bar, -10°C with a mass flow rate of 15 kg/min and is compressed to 12 bar, 140°C. Heat transfer from the compressor to its surroundings occurs at a rate of 6 kW. For steady-state operation, calculate,
(a) the power input to the compressor, in kW, Answer
(b) the entropy production rate, in kW/K, for a control volume encompassing the compressor and its immediate surroundings such that heat transfer occurs at 300 K.
No chatgpt pls will upvote
Shown to the right is a block of mass m=5.71kgm=5.71kg on a ramp that makes an angle θ=24.1∘θ=24.1∘ with the horizontal. This block is being pushed by a horizontal force, F=229NF=229N. The coefficient of kinetic friction between the two surfaces is μ=0.51μ=0.51.
Enter an expression for the acceleration of the block up the ramp using variables from the problem statement together with gg for the acceleration due to gravity.
a=
Chapter 4 Solutions
EBK ESSENTIAL UNIVERSITY PHYSICS, VOLUM
Ch. 4.2 - A curved barrier lies on a horizontal tabletop, as...Ch. 4.2 - A nonzero net force acts on an object. Which of...Ch. 4.4 - A popular childrens book explains the...Ch. 4.5 - For each of the following situations, would the...Ch. 4.6 - The figure shows two blocks with two forces acting...Ch. 4.6 - (1) Would the answer to (a) in Example 4.5 change...Ch. 4 - Distinguish the Aristotelian and Galilean/New...Ch. 4 - A ball bounces off a wall with the same speed it...Ch. 4 - We often use the term inertia to describe human...Ch. 4 - Does a body necessarily move in the direction of...
Ch. 4 - A truck crashes into a stalled car. A student...Ch. 4 - A barefoot astronaut kicks a ball, hard, across a...Ch. 4 - In paddling a canoe, you push water backward with...Ch. 4 - Is it possible for a nonzero net force to act on...Ch. 4 - As your plane accelerates down the runway, you...Ch. 4 - A driver tells passengers to buckle their...Ch. 4 - Section 4.2 Newtons First and Second Laws A subway...Ch. 4 - Prob. 12ECh. 4 - A small plane accelerates down the runway at 7.2...Ch. 4 - A car leaves the road traveling at 110 km/h and...Ch. 4 - Kinesin is a motor protein responsible for moving...Ch. 4 - Starting from rest and undergoing constant...Ch. 4 - In an egg-dropping contest, a student encases an...Ch. 4 - In a front-end collision, a 1300-kg car with...Ch. 4 - Show that the units of acceleration can be written...Ch. 4 - Your spaceship crashes on one of the Suns planets....Ch. 4 - Your friend can barely lift a 35-kg concrete block...Ch. 4 - A cereal box says net weight 340 grams. Whats the...Ch. 4 - Youre a safely engineer for a bridge spanning the...Ch. 4 - The gravitational acceleration at the...Ch. 4 - A 50-kg parachutist descends at a steady 40 km/h....Ch. 4 - A 930-kg motorboat accelerates away from a dock at...Ch. 4 - An elevator accelerates downward at 2.4 m/s2. What...Ch. 4 - At 560 metric tons, the Airbus A-380 is the worlds...Ch. 4 - Find an expression for the thrust (force) of a...Ch. 4 - You slop into an elevator, and it accelerates to a...Ch. 4 - What upward gravitational force does a 5600-kg...Ch. 4 - Your friends mass is 65 kg. If she jumps off a...Ch. 4 - What force is necessary to stretch a spring 48 cm,...Ch. 4 - A 35-N force is applied to a spring with spring...Ch. 4 - A spring with spring constant k = 340 N/m is used...Ch. 4 - Prob. 36ECh. 4 - Prob. 37ECh. 4 - Prob. 38ECh. 4 - Prob. 39ECh. 4 - Prob. 40ECh. 4 - Prob. 41ECh. 4 - Example 4.3: In the 2015 film The Martian, actor...Ch. 4 - Prob. 43ECh. 4 - A 166-g hockey puck is gliding across the ice at...Ch. 4 - An airplane encounters sudden turbulence, and you...Ch. 4 - A 74-kg tree surgeon rides a cherry picker lift to...Ch. 4 - A dancer executes a vertical jump during which the...Ch. 4 - Find expressions for the force needed to bring an...Ch. 4 - An elevator moves upward at 5.2 m/s. Whats its...Ch. 4 - A 2.50-kg object is moving along the x-axis at...Ch. 4 - Blocks of 1.0, 2.0, and 3.0 kg are lined up on a...Ch. 4 - A child pulls an 11-kg wagon with a horizontal...Ch. 4 - Biophysicists use an arrangement of laser beams...Ch. 4 - A force F is applied to a spring of spring...Ch. 4 - A 22(M)-kg airplane pulls two gliders, the first...Ch. 4 - A biologist is studying the growth of rats on the...Ch. 4 - A small car, with mass 945 kg, is stuck on...Ch. 4 - A 2.0-kg mass and a 3.0-kg mass are on a...Ch. 4 - Youre an automotive engineer designing the crumple...Ch. 4 - Frogs tongues dart out to catch insects, with...Ch. 4 - Two large crates, with masses 640 kg and 490 kg,...Ch. 4 - Your engineering firm is asked to specify the...Ch. 4 - With its fuel tanks half full, an F-35A jet...Ch. 4 - Two springs have the same unstretched length but...Ch. 4 - Although we usually write Newtons second law for...Ch. 4 - A railroad car is being pulled beneath a grain...Ch. 4 - A block 20% more massive than you hangs from a...Ch. 4 - Figure 4.27 shows vertical accelerometer data from...Ch. 4 - A hockey stick is in contact with a 165-g puck for...Ch. 4 - After parachuting through the Martian atmosphere,...Ch. 4 - Your airplane is caught in a brief, violent...Ch. 4 -
A hot-air balloon and its basket are accelerating...Ch. 4 - Two masses are joined by a massless string. A 30-N...Ch. 4 - A mass M hangs from a uniform rope of length L and...Ch. 4 - Jerk is the rate of change of acceleration, and...Ch. 4 - Laptop computers are equipped with accelerometers...Ch. 4 - Laptop computers are equipped with accelerometers...Ch. 4 - Laptop computers are equipped with accelerometers...Ch. 4 - Laptop computers are equipped with accelerometers...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Identify each of the following reproductive barriers as prezygotic or postzygotic a. One lilac species lives on...
Campbell Essential Biology (7th Edition)
Pus is both a sign of infection and an indicator of immune defenses in action. Explain.
Campbell Biology (11th Edition)
All of the following processes are involved in the carbon cycle except: a. photosynthesis b. cell respiration c...
Human Biology: Concepts and Current Issues (8th Edition)
18. SCIENTIFIC THINKING By measuring the fossil remains of Homo floresiensis, scientists have estimated its wei...
Campbell Biology: Concepts & Connections (9th Edition)
53. This reaction was monitored as a function of time:
A plot of In[A] versus time yields a straight ...
Chemistry: Structure and Properties (2nd Edition)
What global policy changes and what individual choices can help us sustain the planet that sustains us?
Biology: Life on Earth with Physiology (11th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- If the density and atomic mass of copper are respectively 8.80 x 103 kg/m³ and 63.5 kg/kmol (note that 1 kmol = 1,000 mol), and copper has one free electron per copper atom, determine the following. (a) the drift speed of the electrons in a 10 gauge copper wire (2.588 mm in diameter) carrying a 13.5 A current 1.988-4 See if you can obtain an expression for the drift speed of electrons in a copper wire in terms of the current in the wire, the diameter of the wire, the molecular weight and mass density of copper, Avogadro's number, and the charge on an electron. m/s (b) the Hall voltage if a 2.68 T field is applied perpendicular to the wire 3.34e-6 x Can you start with basic equations for the electric and magnetic forces acting on the electrons moving through the wire and obtain a relationship between the magnitude of the electric and magnetic field and the drift speed of the electrons? How is the magnitude of the electric field related to the Hall voltage and the diameter of the wire? Varrow_forward(a) At what speed (in m/s) will a proton move in a circular path of the same radius as an electron that travels at 7.85 x 100 m/s perpendicular to the Earth's magnetic field at an altitude where the field strength is 1.20 x 10-5 T? 4.27e3 m/s (b) What would the radius (in m) of the path be if the proton had the same speed as the electron? 0.685 x m (c) What would the radius (in m) be if the proton had the same kinetic energy as the electron? 0.0084 m (d) What would the radius (in m) be if the proton had the same momentum as the electron? 0.0303 x marrow_forwardTwo charges are placed on the x axis. One of the charges (91 = +6.63 μC) is at x₁ = +3.00 cm and the other (92 = -24.2 μC) is at x2 = +9.00 cm. Find the net electric field (magnitude and direction given as a plus or minus sign) at (a) x = 0 cm and (b) x = +6.00 cm.arrow_forward
- The diagram shows the all of the forces acting on a body of mass 2.76 kg. The three forces have magnitudes F1 = 65.2 N, F2 = 21.6 N, and F3 = 77.9 N, with directions as indicted in the diagram, where θ = 49.9 degrees and φ = 21.1 degrees. The dashed lines are parallel to the x and y axes. At t = 0, the body is moving at a speed of 6.87 m/s in the positive x direction. a. whats the x component of the acceleration? b. whats the y component of the acceleration? c. whats the speed of the body in m/s at t = 12.3s? d. whats the magnitude of the displacement of the body n meters between t = 0 and 12.3s?arrow_forwardNo chatgpt pls will upvotearrow_forwardNo chatgpt pls will upvotearrow_forward
- A cylinder with a piston contains 0.153 mol of nitrogen at a pressure of 1.83×105 Pa and a temperature of 290 K. The nitrogen may be treated as an ideal gas. The gas is first compressed isobarically to half its original volume. It then expands adiabatically back to its original volume, and finally it is heated isochorically to its original pressure. Part A Compute the temperature at the beginning of the adiabatic expansion. Express your answer in kelvins. ΕΠΙ ΑΣΦ T₁ = ? K Submit Request Answer Part B Compute the temperature at the end of the adiabatic expansion. Express your answer in kelvins. Π ΑΣΦ T₂ = Submit Request Answer Part C Compute the minimum pressure. Express your answer in pascals. ΕΠΙ ΑΣΦ P = Submit Request Answer ? ? K Paarrow_forwardLearning Goal: To understand the meaning and the basic applications of pV diagrams for an ideal gas. As you know, the parameters of an ideal gas are described by the equation pV = nRT, where p is the pressure of the gas, V is the volume of the gas, n is the number of moles, R is the universal gas constant, and T is the absolute temperature of the gas. It follows that, for a portion of an ideal gas, pV = constant. Τ One can see that, if the amount of gas remains constant, it is impossible to change just one parameter of the gas: At least one more parameter would also change. For instance, if the pressure of the gas is changed, we can be sure that either the volume or the temperature of the gas (or, maybe, both!) would also change. To explore these changes, it is often convenient to draw a graph showing one parameter as a function of the other. Although there are many choices of axes, the most common one is a plot of pressure as a function of volume: a pV diagram. In this problem, you…arrow_forwardLearning Goal: To understand the meaning and the basic applications of pV diagrams for an ideal gas. As you know, the parameters of an ideal gas are described by the equation pV = nRT, where p is the pressure of the gas, V is the volume of the gas, n is the number of moles, R is the universal gas constant, and T is the absolute temperature of the gas. It follows that, for a portion of an ideal gas, pV = constant. T One can see that, if the amount of gas remains constant, it is impossible to change just one parameter of the gas: At least one more parameter would also change. For instance, if the pressure of the gas is changed, we can be sure that either the volume or the temperature of the gas (or, maybe, both!) would also change. To explore these changes, it is often convenient to draw a graph showing one parameter as a function of the other. Although there are many choices of axes, the most common one is a plot of pressure as a function of volume: a pV diagram. In this problem, you…arrow_forward
- ■ Review | Constants A cylinder with a movable piston contains 3.75 mol of N2 gas (assumed to behave like an ideal gas). Part A The N2 is heated at constant volume until 1553 J of heat have been added. Calculate the change in temperature. ΜΕ ΑΣΦ AT = Submit Request Answer Part B ? K Suppose the same amount of heat is added to the N2, but this time the gas is allowed to expand while remaining at constant pressure. Calculate the temperature change. AT = Π ΑΣΦ Submit Request Answer Provide Feedback ? K Nextarrow_forward4. I've assembled the following assortment of point charges (-4 μC, +6 μC, and +3 μC) into a rectangle, bringing them together from an initial situation where they were all an infinite distance away from each other. Find the electric potential at point "A" (marked by the X) and tell me how much work it would require to bring a +10.0 μC charge to point A if it started an infinite distance away (assume that the other three charges remains fixed). 300 mm -4 UC "A" 0.400 mm +6 UC +3 UC 5. It's Friday night, and you've got big party plans. What will you do? Why, make a capacitor, of course! You use aluminum foil as the plates, and since a standard roll of aluminum foil is 30.5 cm wide you make the plates of your capacitor each 30.5 cm by 30.5 cm. You separate the plates with regular paper, which has a thickness of 0.125 mm and a dielectric constant of 3.7. What is the capacitance of your capacitor? If you connect it to a 12 V battery, how much charge is stored on either plate? =arrow_forwardLearning Goal: To understand the meaning and the basic applications of pV diagrams for an ideal gas. As you know, the parameters of an ideal gas are described by the equation pV = nRT, where p is the pressure of the gas, V is the volume of the gas, n is the number of moles, R is the universal gas constant, and T is the absolute temperature of the gas. It follows that, for a portion of an ideal gas, PV T = constant. One can see that, if the amount of gas remains constant, it is impossible to change just one parameter of the gas: At least one more parameter would also change. For instance, if the pressure of the gas is changed, we can be sure that either the volume or the temperature of the gas (or, maybe, both!) would also change. To explore these changes, it is often convenient to draw a graph showing one parameter as a function of the other. Although there are many choices of axes, the most common one is a plot of pressure as a function of volume: a pV diagram. In this problem, you…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
Newton's Second Law of Motion: F = ma; Author: Professor Dave explains;https://www.youtube.com/watch?v=xzA6IBWUEDE;License: Standard YouTube License, CC-BY