
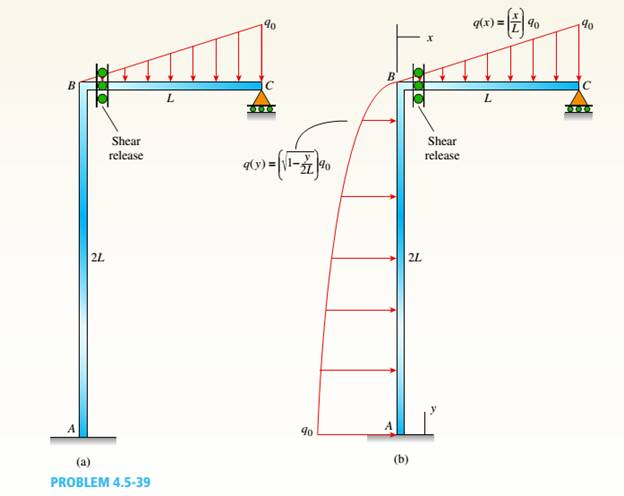
A plane frame (see figure) consists of column AB and beam BC that carries a triangular distributed load (see figure part a). Support A is fixed, and there is a roller support at C. Beam BC has a shear release just right of joint B.
- Find the support reactions at A and C then plot axial-force (N), shear-force (V), and bending-moment (M) diagrams for both members. Label all critical N,K and M values and also the distance to points where any critical ordinates are zero.
a.
The support reaction at point A and C and plot the shear, moment, and axial force diagram.
Answer to Problem 4.5.39P
Explanation of Solution
Given: .
The given figure.
AB column and BC beam forms the plane frame that carries a load that is distributed in the triangular shape. At C there is roller support and support A is fixed. Below the B joint there is a moment release at column AB
Concept Used:
Vertical force equilibrium is given as,
Horizontal force equilibrium is given as,
Calculation: .
Vertical force equilibrium is given as,
Horizontal force equilibrium is given as,
At the top of the moment release the moment is given as,
In equation (1),
Below B there is moment release at point A,
At x the shear force is given and equated to 0,
At point x bending moment is maximum,
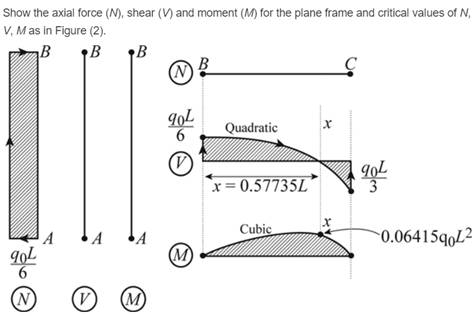
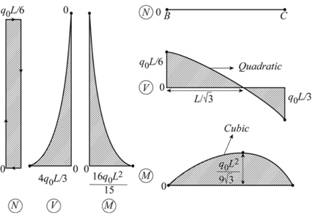
Axial force critical values
Shear force critical values
Moment critical values
Conclusion: .
Thus, the support reaction at point A and C and plot the shear, moment and axial force diagram.
b.
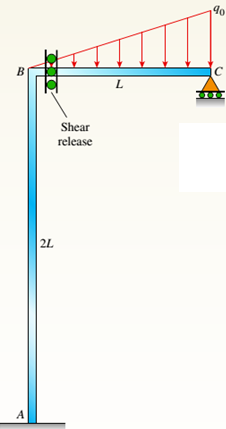
For the load that is parabolic, lateral acts to the right added to AB column and part (a) is repeated.
Answer to Problem 4.5.39P
Explanation of Solution
Given: .
The given figure:.
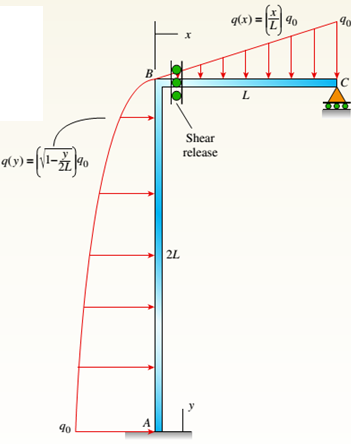
AB column and BC beam forms the plane frame that carries a load that is distributed in the triangular shape. At C there is roller support and support A is fixed. Below the B joint, there is a moment release at column AB.
Concept Used:
Vertical force equilibrium is given as,
Horizontal force equilibrium is given as,
Calculation: .
With the equilibrium force being vertical,
Moment at point B above moment release,
In (2) substitute
With the equilibrium force being horizontal,
As left of x axis is negative,
At A moment below the moment release,
At x shear force is calculated and equated to 0,
At x bending moment is calculated
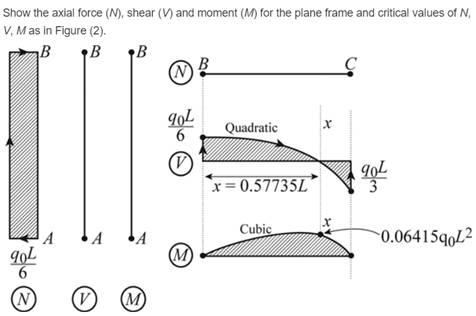
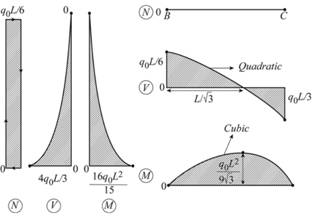
For plane frame and critical values of N, V, M, the axial, shear and moment is given.
Axial force critical values
Shear force critical values in beam
Shear force critical values in column
Moment critical values in beam
Moment critical values in column
Conclusion: .
Thus, for the load that is parabolic lateral acts to the right added to AB column and part (a) is repeated.
Want to see more full solutions like this?
Chapter 4 Solutions
Mechanics of Materials, SI Edition
- what is an air preheater, what are formulas, and their importance, define the diagram, and give me a script on how to explain the design of an air preheater, and how did values end up in that number. based on standardsarrow_forwardQf, Qa,Qm, Qcon,Qfg, Qbd, Qref,Qloss ( meaning, formula, percentage, and importance of higher value na qf, qa etc)arrow_forwardThe beam is supported by a fixed support at point C and a roller at point A. It also has an internal hinge at point B. The beam supports a point load at point D, a moment at point A and a distributed load on segment BC. a. calculate the support reactions at points A and C b. calculate the internal resultant loadings (N, V, M) at points E and F, which lies in the middle between points A and D P = 4 kip Ma = 5 kip-ft w1 = 3 kip/ft and w2 = 4 kip/ft a = 3 ftarrow_forward
- From the image of the pyramid, I want to find what s1 hat, s2 hat, and s3 hat are. I think s3 hat is just equal to e3 hat right? What about the others?arrow_forward(a) What kind of equation is it?(b) Is it linear or non-linear?(c) Is it a coupled system or uncoupled?arrow_forwardWhat kind of system is presented in Figure 2? Open loop or closed loop?arrow_forward
- What are the control hardware shown in the Figure?arrow_forwardQuestion 1. A tube rotates in the horizontal ry plane with a constant angular velocity w about the z-axis. A particle of mass m is released from a radial distance R when the tube is in the position shown. This problem is based on problem 3.2 in the text. R m 2R Figure 1 x a) Draw a free body diagram of the particle if the tube is frictionless. b) Draw a free body diagram of the particle if the coefficient of friction between the sides of the tube and the particle is = k = p. c) For the case where the tube is frictionless, what is the radial speed at which the particle leaves the tube? d) For the case where there is friction, derive a differential equation that would allow you to solve for the radius of the particle as a function of time. I'm only looking for the differential equation. DO NOT solve it. 1 e) If there is no friction, what is the angle of the tube when the particle exits? • Hint: You may need to solve a differential equation for the last part. The "potentially useful…arrow_forwardQuestion 2. A smooth uniform sphere of mass m and radius r is squeezed between two massless levers, each of length 1, which are inclined at an angle with the vertical. A mechanism at pivot point O ensures that the angles & remain the same at all times so that the sphere moves straight upward. This problem is based on Problem 3-1 in the text. P P r Figure 2 a) Draw appropriate freebody diagrams of the system assuming that there is no friction. b) Draw appropriate freebody diagrams of the system assuming that there is a coefficient of friction between the sphere and the right lever of μ. c) If a force P is applied between the ends of the levers (shown in the diagram), and there is no friction, what is the acceleration of the sphere when = 30°arrow_forward
- If you had a matrix A = [1 2 3; 4 5 6; 7 8 9] and a matrix B = [1 2 3], how would you cross multiply them i.e. what is the cross product of AxB. what would be the cross product of a dyadic with a vector?arrow_forwardProblem 3: The inertia matrix can be written in dyadic form which is particularly useful when inertia information is required in various vector bases. On the next page is a right rectangular pyramid of total mass m. Note the location of point Q. (a) Determine the inertia dyadic for the pyramid P, relative to point Q, i.e., 7%, for unit vectors ₁₁, 2, 3.arrow_forwardCan you solve for v? Also, what is A x uarrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
