
Concept explainers
Explanation of Solution
Graph of functions using logarithmic scale:
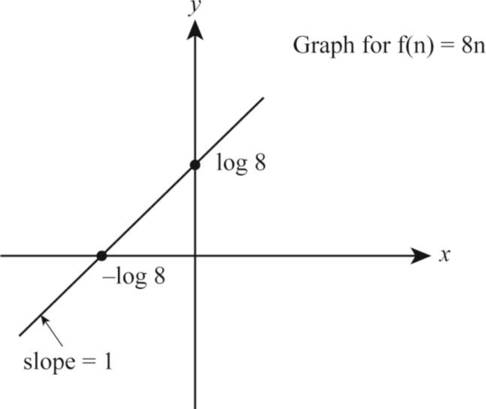
8n:
Let the function be:
Take the logarithm on both the sides of the above function as follows:
According to the given data, let us take
Thus, from the above Equation (2), the value of
The following is the graph representation corresponding to the values
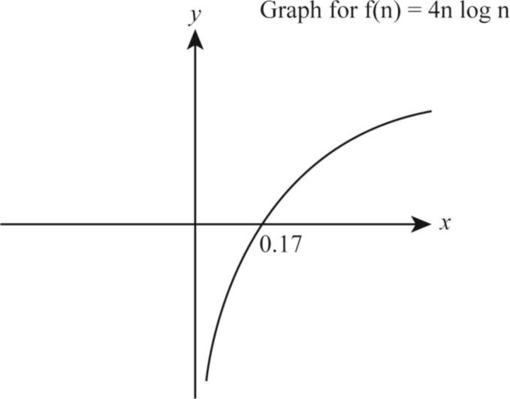
4n logn:
Let the function be:
Take the logarithm on both the sides of the above function as follows:
According to the given data, let us take
The following is the graph representation corresponding for the function
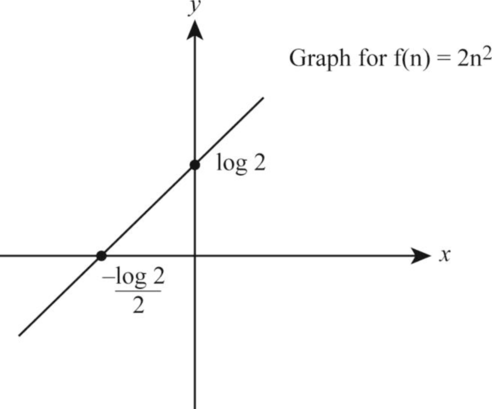
Let the function be:
Take the logarithm on both the sides of the above function as follows:
According to the given data, let us take
Thus, from the above Equation (6), the value of
The following is the graph representation corresponding to the values
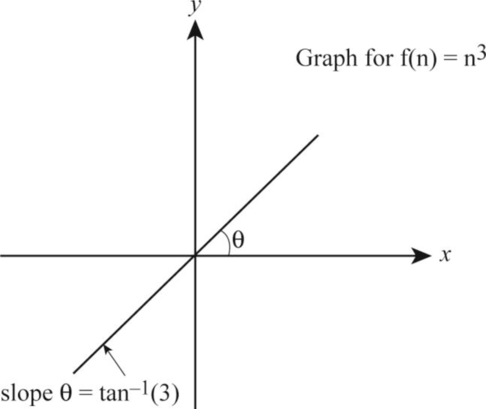
Let the function be:
Take the logarithm on both the sides of the above function as follows:
According to the given data, let us take
The following is the graph representation corresponding to the value on respective x-axis and y-axis respectively.
Let the function be:
Take the logarithm on both the sides of the above function as follows:
According to the given data, let us take
The following is the graph representation corresponding to the value on respective x-axis and y-axis respectively.
Want to see more full solutions like this?
Chapter 4 Solutions
Data Structures and Algorithms in Java
- using r language Obtain a bootstrap t confidence interval estimate for the correlation statistic in Example 8.2 (law data in bootstrap).arrow_forwardusing r language Compute a jackknife estimate of the bias and the standard error of the correlation statistic in Example 8.2.arrow_forwardusing r languagearrow_forward
- using r languagearrow_forwardThe assignment here is to write an app using a database named CIT321 with a collection named students; we will provide a CSV file of the data. You need to use Vue.js to display 2 pages. You should know that this assignment is similar, all too similar in fact, to the cars4sale2 example in the lecture notes for Vue.js 2. You should study that program first. If you figure out cars4sale2, then program 6 will be extremely straightforward. It is not my intent do drop a ton of new material here in the last few days of class. The database contains 51 documents. The first rows of the CSV file look like this: sid last_name 1 Astaire first_name Humphrey CIT major hrs_attempted gpa_points 10 34 2 Bacall Katharine EET 40 128 3 Bergman Bette EET 42 97 4 Bogart Cary CIT 11 33 5 Brando James WEB 59 183 6 Cagney Marlon CIT 13 40 GPA is calculated as gpa_points divided by hrs_attempted. GPA points would have been arrived at by adding 4 points for each credit hour of A, 3 points for each credit hour of…arrow_forwardI need help to solve the following case, thank youarrow_forward
 Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks ColeProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks ColeProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning- COMPREHENSIVE MICROSOFT OFFICE 365 EXCEComputer ScienceISBN:9780357392676Author:FREUND, StevenPublisher:CENGAGE L
 C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning
Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning





